Вектор Лапласа – Рунге – Ленца - Laplace–Runge–Lenz vector

В этой статье векторы и их величины выделены жирным шрифтом и курсивом соответственно. Например, .${\ Displaystyle \ влево | \ mathbf {A} \ right | = A}$

В классической механики , то Лапласа-Рунге-Ленца (НПН) вектор представляет собой вектор используется , главным образом , для описания формы и ориентации орбиты одного астрономического тела вокруг другого, такого как двойной звезды или планеты , вращающейся вокруг звезды. Для двух тел, взаимодействующих под действием силы тяжести Ньютона , вектор LRL является константой движения , что означает, что он одинаков независимо от того, где он рассчитывается на орбите; эквивалентно, вектор LRL называется сохраняющимся . В более общем смысле вектор LRL сохраняется во всех задачах, в которых два тела взаимодействуют посредством центральной силы, которая изменяется как обратный квадрат расстояния между ними; такие проблемы называются проблемами Кеплера .

Атом водорода является задача Кеплера, так как она состоит из двух заряженных частиц , взаимодействующих по закону Кулона в электростатике , другой обратно пропорционально квадрату центральной силы. Вектор LRL был существенным в первом квантовомеханическом выводе спектра атома водорода до разработки уравнения Шредингера . Однако сегодня такой подход используется редко.

В классической и квантовой механике сохраняющиеся величины обычно соответствуют симметрии системы. Сохранение вектора LRL соответствует необычной симметрии; проблема Кеплера математически эквивалентна частице, свободно движущейся по поверхности четырехмерной (гипер-) сферы , так что вся проблема симметрична при определенных поворотах четырехмерного пространства. Эта более высокая симметрия является результатом двух свойств проблемы Кеплера: вектор скорости всегда движется по идеальному кругу, и для данной полной энергии все такие круги скорости пересекаются друг с другом в одних и тех же двух точках.

Вектор Лапласа – Рунге – Ленца назван в честь Пьера-Симона де Лапласа , Карла Рунге и Вильгельма Ленца . Он также известен как вектор Лапласа , с вектором Рунге-Ленца и вектор Ленца . По иронии судьбы, никто из этих ученых этого не обнаружил. Вектор LRL был повторно открыт и переформулирован несколько раз; например, это эквивалентно безразмерная эксцентриситета вектора из небесной механики . Были определены различные обобщения вектора LRL, которые включают эффекты специальной теории относительности , электромагнитных полей и даже различных типов центральных сил.

Контекст

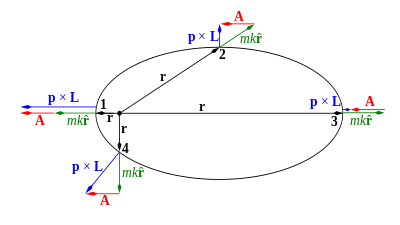
Одна движущаяся частица под любой консервативной центральной силы , имеет , по меньшей мере , четыре константы движения: полную энергию Е и три декартовы компоненты этого углового момента вектор L по отношению к центру силы. Орбита частицы ограничена плоскостью, определяемой начальным импульсом частицы p (или, что то же самое, ее скоростью v ) и вектором r между частицей и центром силы (см. Рисунок 1). Эта плоскость движения перпендикулярна вектору постоянного углового момента L = r × p ; это может быть выражено математически уравнением векторного скалярного произведения r ⋅ L = 0 . Учитывая его математическое определение ниже, вектор Лапласа – Рунге – Ленца (вектор LRL) A всегда перпендикулярен вектору постоянного углового момента L для всех центральных сил ( A ⋅ L = 0 ). Следовательно, А всегда лежит в плоскости движения. Как показано ниже , A указывает от центра силы до перицентра движения, точки наибольшего сближения, а его длина пропорциональна эксцентриситету орбиты.

Вектор A LRL постоянен по длине и направлению, но только для центральной силы, обратной квадрату. Для других центральных сил вектор A непостоянен, но изменяется как по длине, так и по направлению. Если центральная сила приблизительно равна закону обратных квадратов, вектор A приблизительно постоянен по длине, но медленно вращает свое направление. Обобщенный консервативный НПН вектор может быть определены для всех центральных сил, но этот обобщенный вектор является сложной функцией позиции, и , как правило , не экспрессируемым в замкнутой форме . ${\ displaystyle {\ mathcal {A}}}$

Вектор LRL отличается от других сохраняемых величин следующим свойством. В то время как для типичных сохраняющихся величин существует соответствующая циклическая координата в трехмерном лагранжиане системы, такой координаты не существует для вектора LRL. Таким образом, сохранение вектора LRL должно быть получено напрямую, например, методом скобок Пуассона , как описано ниже. Такие сохраняющиеся величины называются «динамическими», в отличие от обычных «геометрических» законов сохранения, например, углового момента.

История повторного открытия

Вектор LRL A является константой движения задачи Кеплера и полезен при описании астрономических орбит, таких как движение планет и двойных звезд. Тем не менее, он никогда не был хорошо известен среди физиков, возможно, потому, что он менее интуитивен, чем импульс и угловой момент. Следовательно, за последние три столетия его независимо открывали несколько раз.

Якоб Герман был первым, кто показал, что A сохраняется для частного случая центральной силы, обратной квадрату, и выяснил ее связь с эксцентриситетом орбитального эллипса . Работа Германа была обобщена до современной формы Иоганном Бернулли в 1710 году. В конце века Пьер-Симон де Лаплас заново открыл сохранение A , выведя его аналитически, а не геометрически. В середине девятнадцатого века Уильям Роуэн Гамильтон вывел эквивалентный вектор эксцентриситета, определенный ниже , используя его, чтобы показать, что вектор импульса p движется по окружности при движении под действием центральной силы, обратной квадрату (рис. 3).

В начале двадцатого века Джозия Уиллард Гиббс получил тот же вектор с помощью векторного анализа . Вывод Гиббса был использован в качестве примера Карлом Рунге в популярном немецком учебнике векторов, на который ссылался Вильгельм Ленц в своей статье о (старой) квантово-механической трактовке атома водорода. В 1926 году Вольфганг Паули использовал вектор LRL для получения уровней энергии атома водорода, используя формулировку квантовой механики матричной механики, после чего он стал известен в основном как вектор Рунге-Ленца .

Математическое определение

Центральная сила, обратная квадрату, действующая на отдельную частицу, описывается уравнением

${\ displaystyle \ mathbf {F} (r) = - {\ frac {k} {r ^ {2}}} \ mathbf {\ hat {r}};}$

Соответствующая потенциальная энергия дается выражением . Постоянный параметр k описывает силу центральной силы; он равен G ⋅ M ⋅ m для гравитационных сил и - k _e ⋅ Q ⋅ q для электростатических сил. Сила притягивает, если k > 0, и отталкивает, если k <0. ${\ displaystyle V (r) = - {\ frac {k} {r}}}$

Рис. 1. Вектор A LRL (показан красным) в четырех точках (обозначенных 1, 2, 3 и 4) на эллиптической орбите связанной точечной частицы, движущейся под действием центральной силы, обратной квадрату. Центр притяжения показан в виде небольшого черного кружка, из которого исходят векторы положения (также черные). Вектор углового момента L перпендикулярен орбите. Компланарные векторы p × L и ( mk / r ) r показаны синим и зеленым цветом соответственно; эти переменные определены ниже . Вектор A постоянен по направлению и величине.

Вектор A LRL математически определяется формулой

куда

• m - масса точечной частицы, движущейся под действием центральной силы,
• p - его вектор импульса,
• L = r × p - его вектор углового момента,
• r - вектор положения частицы (рисунок 1),
• ${\ displaystyle \ mathbf {\ hat {r}}}$- соответствующий единичный вектор , т. е. , и${\ displaystyle \ mathbf {\ hat {r}} = {\ frac {\ mathbf {r}} {r}}}$
• r - величина r , расстояние массы от центра силы.

В системе единиц СИ вектора LRL являются джоуль-килограммовый-метровый (J⋅kg⋅m). Это следует потому, что единицы p и L - это кг⋅м / с и Джс соответственно. Это согласуется с единицами измерения m (кг) и k (Н · м ² ).

Это определение вектора LRL A относится к единственной точечной частице массы m, движущейся под действием фиксированной силы. Однако то же определение можно распространить на проблемы двух тел, такие как проблема Кеплера, если принять m как приведенную массу двух тел и r как вектор между двумя телами.

Поскольку предполагаемая сила консервативна, полная энергия E является константой движения,

${\ displaystyle E = {\ frac {p ^ {2}} {2m}} - {\ frac {k} {r}} = {\ frac {1} {2}} mv ^ {2} - {\ frac {k} {r}}.}$

Предполагаемая сила также является центральной силой. Следовательно, вектор углового момента L также сохраняется и определяет плоскость, в которой движется частица. НПН вектор А перпендикулярен вектора углового момента L , поскольку оба р × L и R перпендикулярны L . Отсюда следует, что A лежит в плоскости движения.

Может быть определены альтернативные составы для одной и той же константы движения, как правило , путем масштабирования вектора с константами, такими , как массы - м , параметр силы к или угловому моменту L . Наиболее распространенный вариант - разделить A на mk , что дает вектор эксцентриситета, безразмерный вектор вдоль большой полуоси, модуль которого равен эксцентриситету коники:

${\ displaystyle \ mathbf {e} = {\ frac {\ mathbf {A}} {mk}} = {\ frac {1} {mk}} (\ mathbf {p} \ times \ mathbf {L}) - \ mathbf {\ hat {r}}.}$

Эквивалентная формулировка умножает этот вектор эксцентриситета на большую полуось a , давая результирующему вектору единицы длины. Еще одна формулировка делит A на , давая эквивалентную сохраняющуюся величину с единицами обратной длины, величину, которая появляется в решении проблемы Кеплера ${\ displaystyle L ^ {2}}$

${\ Displaystyle и \ экв {\ гидроразрыва {1} {r}} = {\ гидроразрыва {км} {L ^ {2}}} + {\ гидроразрыва {A} {L ^ {2}}} \ cos \ theta }$

где - угол между A и вектором положения r . Другие альтернативные составы приведены ниже . ${\ displaystyle \ theta}$

Вывод кеплеровских орбит

Рисунок 2: Упрощенная версия рисунка 1, определяющая угол θ между A и r в одной точке орбиты.

Форма и ориентация орбит могут быть определены из вектора LRL следующим образом . Взяв скалярное произведение A с вектором положения r, получаем уравнение

${\ displaystyle \ mathbf {A} \ cdot \ mathbf {r} = A \ cdot r \ cdot \ cos \ theta = \ mathbf {r} \ cdot \ left (\ mathbf {p} \ times \ mathbf {L} \ справа) -mkr,}$

где θ - угол между r и A (рисунок 2). Перестановка скалярного тройного произведения дает

${\ Displaystyle \ mathbf {r} \ cdot \ left (\ mathbf {p} \ times \ mathbf {L} \ right) = \ left (\ mathbf {r} \ times \ mathbf {p} \ right) \ cdot \ mathbf {L} = \ mathbf {L} \ cdot \ mathbf {L} = L ^ {2}}$

Преобразование дает решение уравнения Кеплера

Это соответствует формуле для конического сечения эксцентриситета e

${\ displaystyle {\ frac {1} {r}} = C \ cdot \ left (1 + e \ cdot \ cos \ theta \ right)}$

где эксцентриситет и C - постоянная величина. ${\ Displaystyle е = {\ гидроразрыва {A} {\ left | mk \ right |}} \ geq 0}$

Если взять скалярное произведение A на себя, получим уравнение, включающее полную энергию E :

${\ displaystyle A ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2},}$

который можно переписать в терминах эксцентриситета,

${\ displaystyle e ^ {2} = 1 + {\ frac {2L ^ {2}} {mk ^ {2}}} E.}$

Таким образом, если энергия E отрицательна (связанные орбиты), эксцентриситет меньше единицы и орбита является эллипсом. И наоборот, если энергия положительна (несвязанные орбиты, также называемые «рассеянными орбитами»), эксцентриситет больше единицы и орбита является гиперболой . Наконец, если энергия точно равна нулю, эксцентриситет равен единице, а орбита представляет собой параболу . Во всех случаях направление A лежит вдоль оси симметрии конического сечения и направлено от центра силы к перицентру, точке наибольшего сближения.

Годографы кругового импульса

Рисунок 3: Вектор импульса p (показан синим) движется по окружности, когда частица движется по эллипсу. Четыре помеченные точки соответствуют точкам на рисунке 1. Круг с центром по оси y в позиции A / L (показан пурпурным) с радиусом mk / L (показан зеленым). Угол η определяет эксцентриситет e эллиптической орбиты (cos  η =  e ). По вписанного угла теоремы для окружностей , η также угол между любой точкой на окружности и двумя точками пересечения с р _х оси, р _х = ± р ₀ , которая зависит только от Е , но не L .

Сохранение вектора A LRL и вектора углового момента L полезно для демонстрации того, что вектор импульса p движется по окружности под действием центральной силы, обратной квадрату.

Взяв точечный продукт

${\ displaystyle mk {\ hat {\ mathbf {r}}} = \ mathbf {p} \ times \ mathbf {L} - \ mathbf {A}}$

с собой дает

${\ displaystyle (mk) ^ {2} = A ^ {2} + p ^ {2} L ^ {2} +2 \ mathbf {L} \ cdot (\ mathbf {p} \ times \ mathbf {A}) .}$

Далее выбирая L вдоль оси z и большую полуось в качестве оси x , получаем уравнение геометрического места для p ,

Другими словами, вектор импульса p ограничен кругом радиуса mk / L = L / ℓ с центром на (0, A / L ) . Эксцентриситет е соответствует косинусу угла η, показанного на рисунке 3.

В вырожденном пределе круговых орбит и, следовательно, обращении в нуль A , окружность центрируется в начале координат (0,0). Для краткости также полезно ввести переменную . ${\ displaystyle p_ {0} = {\ sqrt {2m | E |}}}$

Этот круговой годограф полезен для иллюстрации симметрии проблемы Кеплера.

Константы движения и суперинтегрируемость

Семь скалярных величин E , A и L (будучи векторами, последние две вносят по три сохраняющиеся величины каждая) связаны двумя уравнениями: A ⋅ L = 0 и A ² = m ² k ² + 2 mEL ² , что дает пять независимых констант. движения . (Поскольку величина А , следовательно, эксцентриситет е орбиты, можно определить из полного углового момента L и энергии E , только направление от А сохраняется независимо друг от друга, причем, так как должна быть перпендикулярна к L , оно способствует только одно дополнительное сохраненное количество.)

Это согласуется с шестью начальными условиями (начальное положение частицы и векторы скорости, каждое из которых состоит из трех компонентов), которые определяют орбиту частицы, поскольку начальное время не определяется константой движения. Таким образом, полученная 1-мерная орбита в 6-мерном фазовом пространстве полностью определена.

Механическая система с d степенями свободы может иметь не более 2 d - 1 константы движения, так как есть 2 d начальных условий и начальное время не может быть определено константой движения. Система с более чем d постоянными движения называется суперинтегрируемой, а система с 2 d - 1 константой называется максимально суперинтегрируемой . Поскольку решение уравнения Гамильтона – Якоби в одной системе координат может дать только d констант движения, суперинтегрируемые системы должны быть разделимы более чем в одной системе координат. Задача Кеплера максимально суперинтегрируема, поскольку имеет три степени свободы ( d = 3 ) и пять независимых постоянных движения; его уравнение Гамильтона – Якоби разделимо как в сферических координатах, так и в параболических координатах , как описано ниже .

Максимально суперинтегрируемые системы следуют замкнутым одномерным орбитам в фазовом пространстве , поскольку орбита является пересечением изоповерхностей фазового пространства их констант движения. Следовательно, орбиты перпендикулярны всем градиентам всех этих независимых изоповерхностей, пять в этой конкретной задаче, и, следовательно, определяются обобщенными перекрестными произведениями всех этих градиентов. В результате все суперинтегрируемые системы автоматически описываются механикой Намбу , альтернативой, что эквивалентно гамильтоновой механике .

Максимально суперинтегрируемые системы можно квантовать с помощью коммутационных соотношений , как показано ниже . Тем не менее, эквивалентным образом, они также квантованы в рамках Намбу, например, в этой классической проблеме Кеплера, в квантовый атом водорода.

Эволюция при возмущенных потенциалах

Рисунок 5: Эллиптическая орбита с постепенной прецессией и эксцентриситетом e  = 0,667. Такая прецессия возникает в задаче Кеплера, если центральная сила притяжения слегка отклоняется от закона обратных квадратов. Скорость прецессии можно вычислить с помощью формул в тексте.

Вектор Лапласа – Рунге – Ленца A сохраняется только при идеальной центральной силе, обратной квадрату. Однако в большинстве практических задач, таких как движение планет, потенциальная энергия взаимодействия между двумя телами не является в точности законом обратных квадратов, но может включать дополнительную центральную силу, так называемое возмущение, описываемое потенциальной энергией h ( r ) . В таких случаях вектор LRL медленно вращается в плоскости орбиты, что соответствует медленной апсидальной прецессии орбиты.

По предположению возмущающий потенциал h ( r ) является консервативной центральной силой, что означает, что полная энергия E и вектор углового момента L сохраняются. Таким образом, движение по-прежнему находится в плоскости, перпендикулярной L, и величина A сохраняется из уравнения A ² = m ² k ² + 2 mEL ² . Потенциал возмущения h ( r ) может быть функцией любого вида, но должен быть значительно слабее, чем основная сила обратного квадрата между двумя телами.

Скорость , при которой НПН векторе вращаетс предоставляет информацию о возмущающем потенциале ч ( г ) . Используя каноническую теорию возмущений и координаты действие-угол , легко показать, что A вращается со скоростью

${\ displaystyle {\ begin {align} {\ frac {\ partial} {\ partial L}} \ langle h (r) \ rangle & = \ displaystyle {\ frac {\ partial} {\ partial L}} \ left \ {{\ frac {1} {T}} \ int _ {0} ^ {T} h (r) \, dt \ right \} \\ [1em] & = \ displaystyle {\ frac {\ partial} {\ частичное L}} \ left \ {{\ frac {m} {L ^ {2}}} \ int _ {0} ^ {2 \ pi} r ^ {2} h (r) \, d \ theta \ right \}, \ end {выровнено}}}$

где T - орбитальный период, а тождество L dt = m r ² dθ использовалось для преобразования интеграла по времени в угловой интеграл (рисунок 5). Выражение в угловых скобках, ⟨ ч ( г )⟩ , представляет собой возмущающий потенциал, но в среднем за один полный периода; то есть усредненные по одному полному проходу тела по орбите. Математически это среднее по времени соответствует следующей величине в фигурных скобках. Это усреднение помогает подавить колебания скорости вращения.

Этот подход был использован для помощи проверить Эйнштейн теорию относительности , которая добавляет малое эффективное обратное кубическое возмущение к нормальному ньютоновскому гравитационному потенциалу,

${\ displaystyle h (r) = {\ frac {kL ^ {2}} {m ^ {2} c ^ {2}}} \ left ({\ frac {1} {r ^ {3}}} \ right ).}$

Подставляя эту функцию в интеграл и используя уравнение

${\ displaystyle {\ frac {1} {r}} = {\ frac {mk} {L ^ {2}}} \ left (1 + {\ frac {A} {mk}} \ cos \ theta \ right) }$

чтобы выразить r через θ , скорость прецессии перицентра, вызванная этим неньютоновским возмущением, вычисляется как

${\ displaystyle {\ frac {6 \ pi k ^ {2}} {TL ^ {2} c ^ {2}}},}$

что близко соответствует наблюдаемой аномальной прецессии Меркурия и двойных пульсаров . Это согласие с экспериментом является убедительным доказательством общей теории относительности.

Скобки Пуассона

Немасштабированные функции

Алгебраическая структура задачи, как объясняется в последующих разделах, SO (4) / ℤ ₂ ~ SO (3) × SO (3). Три компоненты L _i вектора углового момента L имеют скобки Пуассона

${\ displaystyle \ {L_ {i}, L_ {j} \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} L_ {s},}$

где i = 1,2,3 и ϵ _ijs - полностью антисимметричный тензор , т. е. символ Леви-Чивиты ; здесь используется индекс суммирования s , чтобы избежать путаницы с параметром силы k, определенным выше . Тогда, поскольку вектор A LRL трансформируется как вектор, мы имеем следующие отношения скобок Пуассона между A и L :

${\ displaystyle \ {A_ {i}, L_ {j} \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} A_ {s}.}$

Наконец, скобки Пуассона между различными компонентами A следующие:

${\ displaystyle \ {A_ {i}, A_ {j} \} = - 2mH \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} L_ {s},}$

где - гамильтониан. Обратите внимание, что промежуток компонентов A и компонентов L не замкнут относительно скобок Пуассона из-за множителя в правой части этого последнего соотношения. ${\ displaystyle H}$${\ displaystyle H}$

Наконец, поскольку и L, и A являются постоянными движения, мы имеем

${\ displaystyle \ {A_ {i}, H \} = \ {L_ {i}, H \} = 0.}$

Скобки Пуассона будут распространены на квантово-механические коммутационные соотношения в следующем разделе и на скобки Ли в следующем разделе .

Масштабированные функции

Как отмечено ниже , масштабированный вектор Лапласа – Рунге – Ленца D может быть определен в тех же единицах, что и угловой момент, путем деления A на . Поскольку D по- прежнему преобразуется как вектор, скобки Пуассона D с вектором углового момента L могут быть записаны в аналогичной форме ${\ displaystyle p_ {0} = {\ sqrt {2m | H |}}}$

${\ displaystyle \ {D_ {i}, L_ {j} \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} D_ {s}.}$

Скобки Пуассона D с собой зависит от знака из H , т.е. от того , энергия отрицательна (продуцирующие закрыты, эллиптические орбиты под обратных квадратов центральной силы) или положительное (производство открытые, гиперболические орбиты под обратных квадратов центральной сила). Для отрицательных энергий, т. Е. Для связанных систем, скобки Пуассона имеют вид

${\ displaystyle \ {D_ {i}, D_ {j} \} = \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} L_ {s}.}$

Теперь мы можем оценить мотивацию выбранного масштабирования D : с этим масштабированием гамильтониан больше не появляется в правой части предыдущего соотношения. Таким образом, оболочка трех компонентов L и трех компонентов D образует шестимерную алгебру Ли под скобкой Пуассона. Эта алгебра Ли изоморфна so (4), алгебре Ли 4-мерной группы вращений SO (4).

Напротив, для положительной энергии скобки Пуассона имеют противоположный знак:

${\ displaystyle \ {D_ {i}, D_ {j} \} = - \ sum _ {s = 1} ^ {3} \ varepsilon _ {ijs} L_ {s}.}$

В этом случае алгебра Ли изоморфна so (3,1).

Различие между положительной и отрицательной энергиями возникает из-за того, что желаемое масштабирование - то, которое исключает гамильтониан из правой части скобок Пуассона между компонентами масштабированного вектора LRL - включает квадратный корень из гамильтониана. Чтобы получить функции с действительными значениями, мы должны затем взять абсолютное значение гамильтониана, который различает положительные значения (где ) и отрицательные значения (где ). ${\ displaystyle | H | = H}$${\ displaystyle | H | = -H}$

Инварианты Казимира и уровни энергии

В инварианты Казимира для отрицательных энергий

${\ Displaystyle C_ {1} = \ mathbf {D} \ cdot \ mathbf {D} + \ mathbf {L} \ cdot \ mathbf {L} = {\ frac {mk ^ {2}} {2 | E |} },}$

${\ Displaystyle C_ {2} = \ mathbf {D} \ cdot \ mathbf {L} = 0,}$

и имеют исчезающие скобки Пуассона со всеми компонентами D и L ,

${\ Displaystyle \ {C_ {1}, L_ {i} \} = \ {C_ {1}, D_ {i} \} = \ {C_ {2}, L_ {i} \} = \ {C_ {2 }, D_ {i} \} = 0.}$

C ₂ тривиально равен нулю, поскольку два вектора всегда перпендикулярны.

Тем не менее, другой инвариант, С ₁ , является нетривиальным и зависит только от т , к и Е . При каноническом квантовании этот инвариант позволяет получить уровни энергии водородоподобных атомов , используя только квантово-механические канонические коммутационные соотношения вместо обычного решения уравнения Шредингера. Этот вывод подробно обсуждается в следующем разделе.

Квантовая механика атома водорода

Рисунок 6: Уровни энергии атома водорода, предсказанные из коммутационных соотношений углового момента и векторных операторов Лапласа – Рунге – Ленца; эти уровни энергии подтверждены экспериментально.

Скобки Пуассона обеспечивают простое руководство для квантования большинства классических систем: отношение коммутации двух квантово-механических операторов задается скобкой Пуассона соответствующих классических переменных, умноженной на iħ .

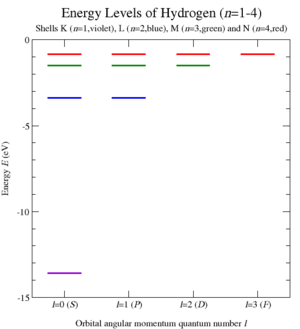
Выполнив это квантование и вычислив собственные значения оператора Казимира C ₁ для задачи Кеплера, Вольфганг Паули смог получить уровни энергии водородоподобных атомов (рис. 6) и, таким образом, их атомный спектр излучения. Этот элегантный вывод 1926 года был получен до разработки уравнения Шредингера .

Тонкость квантово-механического оператора для вектора LRL A состоит в том, что операторы импульса и момента количества движения не коммутируют; следовательно, квантовое операторное произведение p и L должно быть тщательно определено. Обычно операторы для декартовых компонент A _s определяются с помощью симметризованного (эрмитовского) произведения:

${\ displaystyle A_ {s} = - mk {\ hat {r}} _ {s} + {\ frac {1} {2}} \ sum _ {i = 1} ^ {3} \ sum _ {j = 1} ^ {3} \ varepsilon _ {sij} (p_ {i} \ ell _ {j} + \ ell _ {j} p_ {i}),}$

Как только это будет сделано, можно показать, что квантовые операторы LRL удовлетворяют коммутационным соотношениям, точно аналогичным соотношениям скобок Пуассона в предыдущем разделе - просто заменяя скобку Пуассона на коммутатор умножения. ${\ displaystyle 1 / (я \ hbar)}$

Из этих операторов можно определить дополнительные лестничные операторы для L ,

${\ displaystyle J_ {0} = A_ {3},}$

${\ displaystyle J _ {\ pm 1} = \ mp {\ frac {1} {\ sqrt {2}}} \ left (A_ {1} \ pm iA_ {2} \ right).}$

Эти дополнительные Connect различные собственных состояний L ² , так что разные спиновые мультиплеты, между собой.

Нормализованный первый инвариантный оператор Казимира, квантовый аналог вышеупомянутого, может быть определен аналогичным образом:

${\ displaystyle C_ {1} = - {\ frac {mk ^ {2}} {2 \ hbar ^ {2}}} H ^ {- 1} -I,}$

где H ⁻¹ - обратный оператор гамильтоновой энергии, а I - тождественный оператор .

Применение этих лестничных операторов к собственным состояниям | ℓ mn〉 операторов полного углового момента, азимутального углового момента и энергии, собственные значения первого оператора Казимира, C ₁ , квантованы, n ² - 1 . Важно отметить, что благодаря обращению в нуль C ₂ они не зависят от квантовых чисел и m , что приводит к вырождению уровней энергии .

Следовательно, уровни энергии задаются выражением

${\ displaystyle E_ {n} = - {\ frac {mk ^ {2}} {2 \ hbar ^ {2} n ^ {2}}},}$

что совпадает с формулой Ридберга для водородоподобных атомов (рис. 6). Дополнительные операторы симметрии A соединили между собой различные мультиплеты ℓ для заданной энергии (и C ₁ ), определяя n ² состояний на каждом уровне. Фактически они увеличили группу углового момента SO (3) до SO (4) / ℤ ₂ ~ SO (3) × SO (3).

Сохранение и симметрия

Сохранение вектора LRL соответствует тонкой симметрии системы. В классической механике симметрии - это непрерывные операции, которые переводят одну орбиту на другую без изменения энергии системы; в квантовой механике симметрии - это непрерывные операции, которые «смешивают» электронные орбитали с одинаковой энергией, т. е. вырожденные уровни энергии. С такими симметриями обычно связывают сохраняющуюся величину. Например, каждая центральная сила симметрична относительно группы вращений SO (3) , что приводит к сохранению углового момента L . Обычно полное вращение системы не влияет на энергию орбиты; квантово-механически вращение смешивает сферические гармоники с одним и тем же квантовым числом l, не изменяя энергии.

Рисунок 7: Семейство круговых годографов импульса для заданной энергии Е . Все круги проходят через одни и те же две точки на оси p _x (см. Рисунок 3). Это семейство годографов соответствует одному семейству аполлоновских окружностей и σ-изоповерхностям биполярных координат .${\ displaystyle \ pm p_ {0} = \ pm {\ sqrt {2m | E |}}}$

Симметрия центральной силы обратного квадрата выше и тоньше. Своеобразная симметрия задачи Кеплера приводит к сохранению как вектора углового момента L, так и вектора LRL A (как определено выше ) и квантово-механически гарантирует, что уровни энергии водорода не зависят от квантовых чисел углового момента l и м . Однако симметрия более тонкая, потому что операция симметрии должна происходить в многомерном пространстве ; такие симметрии часто называют «скрытыми симметриями».

Классически более высокая симметрия проблемы Кеплера позволяет непрерывно изменять орбиты, сохраняя энергию, но не угловой момент; Другими словами, орбиты с одинаковой энергией, но с разным угловым моментом (эксцентриситетом) могут непрерывно преобразовываться друг в друга. Квантово-механически это соответствует смешиванию орбиталей, которые различаются квантовыми числами l и m , например атомным орбиталям s ( l = 0 ) и p ( l = 1 ). Такое смешивание не может быть выполнено с помощью обычных трехмерных перемещений или вращений, но эквивалентно вращению в более высоком измерении.

Для отрицательных энергий, т. Е. Связанных систем, высшей группой симметрии является SO (4), которая сохраняет длину четырехмерных векторов

${\ displaystyle | \ mathbf {e} | ^ {2} = e_ {1} ^ {2} + e_ {2} ^ {2} + e_ {3} ^ {2} + e_ {4} ^ {2} .}$

В 1935 году Владимир Фок показал, что квантово-механическая ограниченная проблема Кеплера эквивалентна проблеме свободной частицы, ограниченной трехмерной единичной сферой в четырехмерном пространстве. В частности, Фок показал, что волновая функция Шредингера в импульсном пространстве для задачи Кеплера является стереографической проекцией сферических гармоник на сферу. Вращение сферы и повторное проецирование приводит к непрерывному отображению эллиптических орбит без изменения энергии, симметрии SO (4), иногда известной как симметрия Фока ; квантово-механически это соответствует смешиванию всех орбиталей с одинаковым квантовым числом энергии n . Валентин Баргманн впоследствии заметил, что скобки Пуассона для вектора углового момента L и масштабированного вектора LRL A образуют алгебру Ли для SO (4). Проще говоря, шесть величин A и L соответствуют шести сохраняющимся угловым моментам в четырех измерениях, связанных с шестью возможными простыми вращениями в этом пространстве (есть шесть способов выбора двух осей из четырех). Этот вывод не означает, что наша Вселенная является трехмерной сферой; это просто означает, что эта конкретная физическая проблема (задача двух тел для центральных сил с обратным квадратом) математически эквивалентна свободной частице на трехмерной сфере.

Для положительных энергий - то есть, для несвязанных, «разбросанные» системы - чем выше группа симметрии SO (3,1) , который сохраняет длину Минковского из 4-векторов

${\ displaystyle ds ^ {2} = e_ {1} ^ {2} + e_ {2} ^ {2} + e_ {3} ^ {2} -e_ {4} ^ {2}.}$

Случаи как отрицательной, так и положительной энергии рассматривались Фоком и Баргманном и были энциклопедически рассмотрены Бандером и Ициксоном.

Орбиты систем центральных сил - и в частности проблемы Кеплера - также симметричны относительно отражения . Следовательно, упомянутые выше группы SO (3), SO (4) и SO (3,1) не являются полными группами симметрии своих орбит; полные группы - это O (3) , O (4) и O (3,1) соответственно. Тем не менее, только связанные подгруппы SO (3), SO (4) и SO (3,1) необходимы для демонстрации сохранения углового момента и векторов LRL; симметрия отражения не имеет отношения к сохранению, которое может быть получено из алгебры Ли группы.

Вращательная симметрия в четырех измерениях

Рисунок 8: Годографы импульса на рисунке 7 соответствуют стереографическим проекциям больших кругов на трехмерную единичную сферу η. Все большие круги пересекают ось η _x , которая перпендикулярна странице; проекция идет от северного полюса ( единичный вектор w ) на плоскость η _x - η _y , как показано здесь для пурпурного годографа пунктирными черными линиями. Большой круг на широте α соответствует эксцентриситету e = sin α . Цвета больших кругов, показанных здесь, соответствуют соответствующим им годографам на Рисунке 7.

Связь между проблемой Кеплера и четырехмерной вращательной симметрией SO (4) легко наглядно представить. Обозначим четырехмерные декартовы координаты ( w , x , y , z ), где ( x , y , z ) представляют декартовы координаты вектора нормального положения r . Трехмерный вектор импульса p связан с четырехмерным вектором на трехмерной единичной сфере ${\ displaystyle {\ boldsymbol {\ eta}}}$

${\ displaystyle {\ begin {align} {\ boldsymbol {\ eta}} & = \ displaystyle {\ frac {p ^ {2} -p_ {0} ^ {2}} {p ^ {2} + p_ {0 } ^ {2}}} \ mathbf {\ hat {w}} + {\ frac {2p_ {0}} {p ^ {2} + p_ {0} ^ {2}}} \ mathbf {p} \\ [1em] & = \ displaystyle {\ frac {mk-rp_ {0} ^ {2}} {mk}} \ mathbf {\ hat {w}} + {\ frac {rp_ {0}} {mk}} \ mathbf {p}, \ end {выравнивается}}}$

где - единичный вектор вдоль новой оси w . Отображение преобразования p в η можно однозначно инвертировать; например, x- компонента импульса равна ${\ displaystyle \ mathbf {\ hat {w}}}$

${\ displaystyle p_ {x} = p_ {0} {\ frac {\ eta _ {x}} {1- \ eta _ {w}}},}$

и аналогично для p _y и p _z . Другими словами, трехмерный вектор p представляет собой стереографическую проекцию четырехмерного вектора, масштабированного на p ₀ (рисунок 8). ${\ displaystyle {\ boldsymbol {\ eta}}}$

Без потери общности, мы можем устранить нормальную вращательную симметрию, выбрав декартовы координаты так, чтобы ось z была выровнена с вектором углового момента L, а годографы импульса выровнены, как на рисунке 7, с центрами окружностей на у оси. Поскольку движение является плоским, а p и L перпендикулярны, p _z = η _z = 0, и внимание может быть ограничено трехмерным вектором = ( η _w , η _x , η _y ) . Семейство аполлоновских окружностей годографов импульса (рис.7) соответствует семейству больших окружностей на трехмерной сфере, каждая из которых пересекает ось η _x в двух фокусах η _x = ± 1 , соответствующих фокусам годографа импульса. при p _x = ± p ₀ . Эти большие круги связаны простым вращением вокруг оси η _x (рис. 8). Эта вращательная симметрия преобразует все орбиты с одной и той же энергией друг в друга; однако такой поворот ортогонален обычным трехмерным поворотам, поскольку он преобразует четвертое измерение η _w . Эта более высокая симметрия характерна для задачи Кеплера и соответствует сохранению вектора LRL. ${\ displaystyle {\ boldsymbol {\ eta}}}$${\ displaystyle {\ boldsymbol {\ eta}}}$

Элегантное решение с переменными действие-угол для задачи Кеплера может быть получено путем исключения избыточных четырехмерных координат в пользу эллиптических цилиндрических координат ( χ , ψ , φ ).${\ displaystyle {\ boldsymbol {\ eta}}}$

${\ displaystyle \ eta _ {w} = \ operatorname {cn} \ chi \ operatorname {cn} \ psi,}$

${\ displaystyle \ eta _ {x} = \ operatorname {sn} \, \ chi \ operatorname {dn} \ psi \, \ cos \ phi,}$

${\ displaystyle \ eta _ {y} = \ operatorname {sn} \ chi \ operatorname {dn} \ psi \ sin \ phi,}$

${\ displaystyle \ eta _ {z} = \ operatorname {dn} \ chi \ operatorname {sn} \ psi,}$

где sn, cn и dn - эллиптические функции Якоби .

Обобщения на другие потенциалы и относительность

Вектор Лапласа – Рунге – Ленца также можно обобщить для определения сохраняющихся величин, применимых к другим ситуациям.

При наличии однородного электрического поля E обобщенный вектор Лапласа – Рунге – Ленца имеет вид ${\ displaystyle {\ mathcal {A}}}$

${\ Displaystyle {\ mathcal {A}} = \ mathbf {A} + {\ frac {mq} {2}} \ left [\ left (\ mathbf {r} \ times \ mathbf {E} \ right) \ раз \ mathbf {r} \ right],}$

где q - заряд вращающейся частицы. Хотя он и не сохраняется, он дает начало сохраняющейся величине, а именно . ${\ displaystyle {\ mathcal {A}}}$${\ Displaystyle {\ mathcal {A}} \ cdot \ mathbf {E}}$

Дальнейшее обобщение вектора Лапласа – Рунге – Ленца на другие потенциалы и специальную теорию относительности , наиболее общая форма может быть записана как

${\ displaystyle {\ mathcal {A}} = \ left ({\ frac {\ partial \ xi} {\ partial u}} \ right) \ left (\ mathbf {p} \ times \ mathbf {L} \ right) + \ left [\ xi -u \ left ({\ frac {\ partial \ xi} {\ partial u}} \ right) \ right] L ^ {2} \ mathbf {\ hat {r}},}$

где u = 1 / r и ξ = cos θ , причем угол θ определяется формулой

${\ displaystyle \ theta = L \ int ^ {u} {\ frac {du} {\ sqrt {m ^ {2} c ^ {2} (\ gamma ^ {2} -1) -L ^ {2} u ^ {2}}}},}$

и γ является фактор Лоренца . Как и раньше, мы можем получить сохраняющийся бинормальный вектор B , взяв векторное произведение с сохраняющимся вектором углового момента

${\ displaystyle {\ mathcal {B}} = \ mathbf {L} \ times {\ mathcal {A}}.}$

Эти два вектора можно также объединить в сохраняющийся диадический тензор W ,

${\ displaystyle {\ mathcal {W}} = \ alpha {\ mathcal {A}} \ otimes {\ mathcal {A}} + \ beta \, {\ mathcal {B}} \ otimes {\ mathcal {B}} .}$

На иллюстрации можно вычислить вектор LRL для нерелятивистского изотропного гармонического осциллятора. Поскольку сила центральная,

${\ Displaystyle \ mathbf {F} (г) = - к \ mathbf {г},}$

вектор момента импульса сохраняется и движение лежит в плоскости.

Сохраняющийся диадический тензор можно записать в простой форме

${\ displaystyle {\ mathcal {W}} = {\ frac {1} {2m}} \ mathbf {p} \ otimes \ mathbf {p} + {\ frac {k} {2}} \, \ mathbf {r } \ otimes \ mathbf {r},}$

хотя p и r не обязательно перпендикулярны.

Соответствующий вектор Рунге – Ленца более сложен:

${\ displaystyle {\ mathcal {A}} = {\ frac {1} {\ sqrt {mr ^ {2} \ omega _ {0} A-mr ^ {2} E + L ^ {2}}}} \ left \ {\ left (\ mathbf {p} \ times \ mathbf {L} \ right) + \ left (mr \ omega _ {0} A-mrE \ right) \ mathbf {\ hat {r}} \ right \ },}$

куда

${\ displaystyle \ omega _ {0} = {\ sqrt {\ frac {k} {m}}}}$

- собственная частота колебаний, а

${\ displaystyle A = (E ^ {2} - \ omega ^ {2} L ^ {2}) ^ {1/2} / \ omega.}$

Доказательства сохранения вектора Лапласа – Рунге – Ленца в задачах Кеплера.

Ниже приведены аргументы, показывающие, что вектор LRL сохраняется под действием центральных сил, которые подчиняются закону обратных квадратов.

Прямое доказательство сохранения

Центральная сила, действующая на частицу, равна ${\ displaystyle \ mathbf {F}}$

${\ displaystyle \ mathbf {F} = {\ frac {d \ mathbf {p}} {dt}} = f (r) {\ frac {\ mathbf {r}} {r}} = f (r) \ mathbf {\ hat {r}}}$

для некоторой функции радиуса . Поскольку угловой момент сохраняется под действием центральных сил, и ${\ displaystyle f (r)}$${\ displaystyle r}$${\ Displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p}}$${\ displaystyle {\ frac {d} {dt}} \ mathbf {L} = 0}$

${\ displaystyle {\ frac {d} {dt}} \ left (\ mathbf {p} \ times \ mathbf {L} \ right) = {\ frac {d \ mathbf {p}} {dt}} \ times \ mathbf {L} = f (r) \ mathbf {\ hat {r}} \ times \ left (\ mathbf {r} \ times m {\ frac {d \ mathbf {r}} {dt}} \ right) = f (r) {\ frac {m} {r}} \ left [\ mathbf {r} \ left (\ mathbf {r} \ cdot {\ frac {d \ mathbf {r}} {dt}} \ right) -r ^ {2} {\ frac {d \ mathbf {r}} {dt}} \ right],}$

где импульс и где тройное перекрестное произведение было упрощено с использованием формулы Лагранжа${\ displaystyle \ mathbf {p} = m {\ frac {d \ mathbf {r}} {dt}}}$

${\ displaystyle \ mathbf {r} \ times \ left (\ mathbf {r} \ times {\ frac {d \ mathbf {r}} {dt}} \ right) = \ mathbf {r} \ left (\ mathbf { r} \ cdot {\ frac {d \ mathbf {r}} {dt}} \ right) -r ^ {2} {\ frac {d \ mathbf {r}} {dt}}.}$

Личность

${\ displaystyle {\ frac {d} {dt}} \ left (\ mathbf {r} \ cdot \ mathbf {r} \ right) = 2 \ mathbf {r} \ cdot {\ frac {d \ mathbf {r} } {dt}} = {\ frac {d} {dt}} (r ^ {2}) = 2r {\ frac {dr} {dt}}}$

дает уравнение

${\ displaystyle {\ frac {d} {dt}} \ left (\ mathbf {p} \ times \ mathbf {L} \ right) = - mf (r) r ^ {2} \ left [{\ frac {1 } {r}} {\ frac {d \ mathbf {r}} {dt}} - {\ frac {\ mathbf {r}} {r ^ {2}}} {\ frac {dr} {dt}} \ right] = - mf (r) r ^ {2} {\ frac {d} {dt}} \ left ({\ frac {\ mathbf {r}} {r}} \ right).}$

Для частного случая центральной силы обратного квадрата это равно ${\ displaystyle f (r) = {\ frac {-k} {r ^ {2}}}}$

${\ displaystyle {\ frac {d} {dt}} \ left (\ mathbf {p} \ times \ mathbf {L} \ right) = mk {\ frac {d} {dt}} \ left ({\ frac { \ mathbf {r}} {r}} \ right) = {\ frac {d} {dt}} (mk \ mathbf {\ hat {r}}).}$

Следовательно, A сохраняется для центральных сил, обратных квадрату

${\ displaystyle {\ frac {d} {dt}} \ mathbf {A} = {\ frac {d} {dt}} \ left (\ mathbf {p} \ times \ mathbf {L} \ right) - {\ frac {d} {dt}} \ left (mk \ mathbf {\ hat {r}} \ right) = \ mathbf {0}.}$

Более короткое доказательство получается при использовании отношения углового момента к угловой скорости , которое справедливо для частицы, движущейся в плоскости, перпендикулярной к . В зависимости от центральных сил, обратных квадрату, производная по времени равна ${\ displaystyle \ mathbf {L} = мистер ^ {2} {\ boldsymbol {\ omega}}}$${\ displaystyle \ mathbf {L}}$${\ Displaystyle \ mathbf {p} \ times \ mathbf {L}}$

${\ displaystyle {\ frac {d} {dt}} \ mathbf {p} \ times \ mathbf {L} = \ left ({\ frac {-k} {r ^ {2}}} \ mathbf {\ hat { r}} \ right) \ times \ left (mr ^ {2} {\ boldsymbol {\ omega}} \ right) = mk \, {\ boldsymbol {\ omega}} \ times \ mathbf {\ hat {r}} = mk \, {\ frac {d} {dt}} \ mathbf {\ hat {r}},}$

где последнее равенство выполняется, потому что единичный вектор может изменяться только при вращении, и является орбитальной скоростью вращающегося вектора. Таким образом, A рассматривается как разность двух векторов с равными производными по времени. ${\ displaystyle {\ boldsymbol {\ omega}} \ times \ mathbf {\ hat {r}}}$

Как описано в другом месте этой статьи , этот вектор A LRL является частным случаем общего сохраняющегося вектора, который может быть определен для всех центральных сил. Однако, поскольку большинство центральных сил не создают замкнутых орбит (см . Теорему Бертрана ), аналогичный вектор редко имеет простое определение и обычно является многозначной функцией угла θ между r и . ${\ displaystyle {\ mathcal {A}}}$${\ displaystyle {\ mathcal {A}}}$${\ displaystyle {\ mathcal {A}}}$

Уравнение Гамильтона – Якоби в параболических координатах

Постоянство вектора LRL также может быть получено из уравнения Гамильтона – Якоби в параболических координатах ( ξ , η ) , которые определяются уравнениями

${\ Displaystyle \ xi = г + х,}$

${\ displaystyle \ eta = rx,}$

где r представляет собой радиус в плоскости орбиты

${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}.}$

Обращение этих координат есть

${\ Displaystyle х = {\ гидроразрыва {1} {2}} (\ xi - \ eta),}$

${\ displaystyle y = {\ sqrt {\ xi \ eta}},}$

Разделение уравнения Гамильтона – Якоби в этих координатах дает два эквивалентных уравнения

${\ Displaystyle 2 \ xi p _ {\ xi} ^ {2} -mk-mE \ xi = - \ Gamma,}$

${\ displaystyle 2 \ eta p _ {\ eta} ^ {2} -mk-mE \ eta = \ Gamma,}$

где Γ - постоянная движения. Вычитание и повторное выражение в терминах декартовых импульсов p _x и p _y показывает, что Γ эквивалентно вектору LRL

${\ displaystyle \ Gamma = p_ {y} (xp_ {y} -yp_ {x}) - mk {\ frac {x} {r}} = A_ {x}.}$

Теорема Нётер

Связь между вращательной симметрией, описанной выше, и сохранением вектора LRL может быть сделана количественной с помощью теоремы Нётер . Эта теорема, которая используется для нахождения постоянных движения, утверждает, что любое бесконечно малое изменение обобщенных координат физической системы

${\ displaystyle \ delta q_ {i} = \ varepsilon g_ {i} (\ mathbf {q}, \ mathbf {\ dot {q}}, t)}$

что приводит к изменению лагранжиана до первого порядка по полной производной по времени

${\ displaystyle \ delta L = \ varepsilon {\ frac {d} {dt}} G (\ mathbf {q}, t)}$

соответствует сохраняющейся величине Γ

${\ displaystyle \ Gamma = -G + \ sum _ {i} g_ {i} \ left ({\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}} \ right).}$

В частности, сохраняющаяся компонента вектора LRL A _s соответствует изменению координат

${\ displaystyle \ delta _ {s} x_ {i} = {\ frac {\ varepsilon} {2}} \ left [2p_ {i} x_ {s} -x_ {i} p_ {s} - \ delta _ { is} \ left (\ mathbf {r} \ cdot \ mathbf {p} \ right) \ right],}$

где i равно 1, 2 и 3, причем x _i и p _i - i- е компоненты векторов положения и импульса r и p , соответственно; как обычно, δ _{является} представляет Кронекера . Результирующее изменение первого порядка в лагранжиане равно

${\ displaystyle \ delta L = {\ frac {1} {2}} \ varepsilon mk {\ frac {d} {dt}} \ left ({\ frac {x_ {s}} {r}} \ right). }$

Подстановка в общую формулу для сохраняющейся величины Γ дает сохраняющуюся компоненту A _s вектора LRL:

${\ Displaystyle A_ {s} = \ left [p ^ {2} x_ {s} -p_ {s} \ left (\ mathbf {r} \ cdot \ mathbf {p} \ right) \ right] -mk \ left ({\ frac {x_ {s}} {r}} \ right) = \ left [\ mathbf {p} \ times \ left (\ mathbf {r} \ times \ mathbf {p} \ right) \ right] _ {s} -mk \ left ({\ frac {x_ {s}} {r}} \ right).}$

Трансформация лжи

Рисунок 9: Преобразование Ли, из которого выводится сохранение вектора A LRL . При изменении параметра масштабирования λ энергия и угловой момент изменяются, но эксцентриситет e, а также величина и направление A остаются неизменными.

Нётер вывод сохранения НПН вектор А элегантен, но имеет один недостаток: координата вариация ? X _я включаю в себя не только позицию г , но и импульс р или, что эквивалентно, скорость V . Этот недостаток может быть устранен, если вместо этого вывести сохранение A с использованием подхода, впервые предложенного Софусом Ли . В частности, можно определить преобразование Ли, в котором координаты r и время t масштабируются различными степенями параметра λ (рисунок 9),

${\ displaystyle t \ rightarrow \ lambda ^ {3} t, \ qquad \ mathbf {r} \ rightarrow \ lambda ^ {2} \ mathbf {r}, \ qquad \ mathbf {p} \ rightarrow {\ frac {1} {\ lambda}} \ mathbf {p}.}$

Это преобразование изменяет полный угловой момент L и энергию E ,

${\ Displaystyle L \ rightarrow \ lambda L, \ qquad E \ rightarrow {\ frac {1} {\ lambda ^ {2}}} E,}$

но сохраняет свой продукт EL ² . Следовательно, эксцентриситет e и величина A сохраняются, как видно из уравнения для A ²

${\ displaystyle A ^ {2} = m ^ {2} k ^ {2} e ^ {2} = m ^ {2} k ^ {2} + 2mEL ^ {2}.}$

Направление A также сохраняется, поскольку полуоси не изменяются глобальным масштабированием. Это преобразование также сохраняет третий закон Кеплера , а именно, что полуось a и период T образуют постоянную  T ² / a ³ .

Альтернативные масштабы, символы и формулировки

В отличие от векторов импульса и момента импульса p и L , общепринятого определения вектора Лапласа – Рунге – Ленца не существует; В научной литературе используется несколько различных коэффициентов масштабирования и символов. Наиболее распространенное определение дано выше , но другой распространенной альтернативой является деление на константу mk, чтобы получить безразмерный вектор сохраняющегося эксцентриситета

${\ displaystyle \ mathbf {e} = {\ frac {1} {mk}} \ left (\ mathbf {p} \ times \ mathbf {L} \ right) - \ mathbf {\ hat {r}} = {\ frac {m} {k}} \ left (\ mathbf {v} \ times \ left (\ mathbf {r} \ times \ mathbf {v} \ right) \ right) - \ mathbf {\ hat {r}}, }$

где v - вектор скорости. Этот масштабированный вектор e имеет то же направление, что и A, и его величина равна эксцентриситету орбиты и, таким образом, равна нулю для круговых орбит.

Другая масштабируются версия также возможна, например, путем деления А на м в одиночку

${\ displaystyle \ mathbf {M} = \ mathbf {v} \ times \ mathbf {L} -k \ mathbf {\ hat {r}},}$

или по p ₀

${\ displaystyle \ mathbf {D} = {\ frac {\ mathbf {A}} {p_ {0}}} = {\ frac {1} {\ sqrt {2m | E |}}} \ left \ {\ mathbf {p} \ times \ mathbf {L} -mk \ mathbf {\ hat {r}} \ right \},}$

который имеет те же единицы вектора кинетического момента L .

В редких случаях знак вектора LRL может быть изменен на противоположный, то есть масштабироваться на -1. Другие общие символы для вектора LRL включают в , R , F , J и V . Однако выбор масштабирования и символа для вектора LRL не влияет на его сохранение.

Рисунок 4: Вектор углового момента L , вектор LRL A и вектор Гамильтона, бинормаль B , взаимно перпендикулярны; A и B указывают на большую и малую оси, соответственно, эллиптической орбиты задачи Кеплера.

Альтернативным сохраняющимся вектором является бинормальный вектор B, изученный Уильямом Роуэном Гамильтоном,

который сохраняется и указывает на малую полуось эллипса. (Это не определено для исчезающего эксцентриситета.)

Вектор LRL A = B × L - это векторное произведение B и L (рисунок 4). На импульсном годографе в соответствующем разделе выше, Б легко видеть , чтобы соединить происхождение импульсов с центром кругового годографа, и обладать величиной A / L . В перигелии он указывает в направлении импульса.

Вектор B обозначаются как «бинормаль» , поскольку она перпендикулярна как A и L . Подобно самому вектору LRL, бинормальный вектор может быть определен с различными масштабами и символами.

Два консервативных вектора, A и B, могут быть объединены, чтобы сформировать консервативный диадический тензор W ,

${\ displaystyle \ mathbf {W} = \ alpha \ mathbf {A} \ otimes \ mathbf {A} + \ beta \, \ mathbf {B} \ otimes \ mathbf {B},}$

где α и β - произвольные масштабные константы и представляют собой тензорное произведение (которое не связано с векторным кросс-произведением , несмотря на их аналогичный символ). Написанное в явных компонентах, это уравнение имеет вид ${\ displaystyle \ otimes}$

${\ displaystyle W_ {ij} = \ alpha A_ {i} A_ {j} + \ beta B_ {i} B_ {j}.}$

Поскольку векторы A и B перпендикулярны друг другу, их можно рассматривать как главные оси сохраняющегося тензора W , то есть его масштабированные собственные векторы . W перпендикулярно L ,

${\ displaystyle \ mathbf {L} \ cdot \ mathbf {W} = \ alpha \ left (\ mathbf {L} \ cdot \ mathbf {A} \ right) \ mathbf {A} + \ beta \ left (\ mathbf { L} \ cdot \ mathbf {B} \ right) \ mathbf {B} = 0,}$

поскольку A и B оба перпендикулярны L , L ⋅ A = L ⋅ B = 0 .

Более конкретно, это уравнение в явных компонентах читается так:

${\ displaystyle \ left (\ mathbf {L} \ cdot \ mathbf {W} \ right) _ {j} = \ alpha \ left (\ sum _ {i = 1} ^ {3} L_ {i} A_ {i } \ right) A_ {j} + \ beta \ left (\ sum _ {i = 1} ^ {3} L_ {i} B_ {i} \ right) B_ {j} = 0.}$

Смотрите также

• Астродинамика : орбита , вектор эксцентриситета , элементы орбиты.
• Теорема Бертрана
• Уравнение Бине
• Проблема двух тел

использованная литература

дальнейшее чтение

• Баэз, Джон (2008). «Новый взгляд на проблему Кеплера: вектор Лапласа – Рунге – Ленца» (PDF) . Проверено 31 мая 2021 .
• Баэз, Джон (2003). «Тайны гравитационной задачи двух тел» . Архивировано из оригинала на 2008-10-21 . Проверено 11 декабря 2004 .
• Баэз, Джон (2018). «Тайны гравитационной задачи двух тел» . Проверено 31 мая 2021 . Обновленная версия предыдущего источника.
• Д'Элизео, ММ (2007). «Орбитальное уравнение первого порядка». Американский журнал физики . 75 (4): 352–355. Bibcode : 2007AmJPh..75..352D . DOI : 10.1119 / 1.2432126 .
• Холл, Брайан К. (2013), Квантовая теория для математиков , Тексты для выпускников по математике, 267 , Springer, ISBN 978-1461471158.
• Выщелачивание, PGL; ГП Флессас (2003). «Обобщения вектора Лапласа – Рунге – Ленца». J. Нелинейная математика. Phys . 10 (3): 340–423. arXiv : math-ph / 0403028 . Bibcode : 2003JNMP ... 10..340L . DOI : 10.2991 / jnmp.2003.10.3.6 . S2CID  73707398 .