Эта статья про геометрическую фигуру. Для использования в других целях, см
Эллипс (значения) .
Плоская кривая: коническое сечение

Эллипс (красный), полученный как пересечение
конуса с наклонной плоскостью.

Эллипсы: примеры с возрастающим эксцентриситетом
В математике , эллипс является плоской кривой окружающих два координационные центры , такие , что для всех точек на кривой, сумма двух расстояний до фокальных точек является константой. Таким образом, он представляет собой круг , представляющий собой особый тип эллипса, в котором две точки фокусировки совпадают. Удлинение эллипса измеряется его эксцентриситетом , числом от ( предельный случай круга) до (предельный случай бесконечного удлинения, уже не эллипс, а парабола ).



Эллипс имеет простое алгебраическое решение для своей площади, но только приближения для его периметра (также известного как окружность ), для которого требуется интегрирование для получения точного решения.
Аналитически уравнение стандартного эллипса с центром в начале координат с шириной и высотой имеет следующий вид:



Если предположить , что фокусы для . Стандартное параметрическое уравнение:




Эллипсы - это замкнутый тип конического сечения : плоская кривая, отслеживающая пересечение конуса с плоскостью (см. Рисунок). Эллипсы имеют много общего с двумя другими формами конических сечений, параболами и гиперболами , которые являются открытыми и неограниченными . Под углом сечение из цилиндра также эллипс.
Эллипс также может быть определен в терминах одной фокальной точки и линии вне эллипса, называемой директрисой : для всех точек на эллипсе соотношение между расстоянием до фокуса и расстоянием до директрисы является постоянным. Это постоянное соотношение и есть упомянутый выше эксцентриситет:

Эллипсы распространены в физике , астрономии и технике . Например, орбита каждой планеты в солнечной системе представляет собой приблизительно эллипс с Солнцем в одной точке фокусировки (точнее, фокус - это барицентр пары Солнце – планета). То же самое верно для спутников, вращающихся вокруг планет, и всех других систем двух астрономических тел. Формы планет и звезд часто хорошо описываются эллипсоидами . Круг, рассматриваемый под боковым углом, выглядит как эллипс: то есть эллипс - это изображение круга при параллельной или перспективной проекции . Эллипс также является простейшей фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения представляют собой синусоиды с одинаковой частотой: аналогичный эффект приводит к эллиптической поляризации света в оптике .
Название ἔλλειψις ( élleipsis , «упущение») было дано Аполлонием Пергским в его « Кониках» .
Определение как геометрическое место точек

Эллипс: определение по сумме расстояний до фокусов

Эллипс: определение по фокусу и круговой направляющей
Эллипс может быть определен геометрически как набор или геометрическое место точек на евклидовой плоскости:
- Учитывая две фиксированные точки, называемые фокусами, и расстояние, которое больше, чем расстояние между фокусами, эллипс - это набор точек , сумма расстояний которых равна :






Середина отрезка прямой, соединяющего фокусы, называется центром эллипса. Линия, проходящая через фокусы, называется большой осью , а линия, перпендикулярная ей, проходящая через центр, - малой осью . Большая ось пересекает эллипс в двух вершинах , находящихся на расстоянии до центра. Расстояние фокусов до центра называется фокусным расстоянием или линейным эксцентриситетом. Частное - это эксцентриситет .
Большая ось пересекает эллипс в двух вершинах , находящихся на расстоянии до центра. Расстояние фокусов до центра называется фокусным расстоянием или линейным эксцентриситетом. Частное - это эксцентриситет .




Корпус представляет собой круг и включен как особый тип эллипса.

Уравнение можно посмотреть по-другому (см. Рисунок):

- Если это круг со средней точкой и радиусом , то расстояние от точки до круга равно расстоянию до фокуса :







 называется круговой направляющей (относящейся к фокусу ) эллипса. Это свойство не следует путать с определением эллипса с помощью прямой линии ниже.
называется круговой направляющей (относящейся к фокусу ) эллипса. Это свойство не следует путать с определением эллипса с помощью прямой линии ниже.

Используя сферы Данделина , можно доказать, что любое плоское сечение конуса с плоскостью является эллипсом, если предположить, что плоскость не содержит вершины и имеет наклон меньше, чем у линий на конусе.
В декартовых координатах
Стандартное уравнение
Стандартная форма эллипса в декартовых координатах предполагает, что начало координат - центр эллипса, ось x - большая ось, и:
- фокусы - это точки ,

- вершины есть .

Для произвольной точки расстояния до фокуса является
и другим фокусом . Следовательно, точка находится на эллипсе всякий раз, когда:






Удаление радикалов подходящими квадратами и использованием дает стандартное уравнение эллипса:


или, решенный для y:

Параметры ширины и высоты называются большой и малой полуосями . Верхняя и нижняя точки - это совпадения вершин . Расстояния от точки эллипса до левого и правого фокусов равны и .





Из уравнения следует, что эллипс симметричен относительно координатных осей и, следовательно, относительно начала координат.
Параметры
Основные оси
В данной статье, полуглавные и полуавтоматические малые оси обозначены и , соответственно, т.е.


В принципе, каноническое уравнение эллипса может иметь (и, следовательно, эллипс будет больше, чем ширина). Эта форма может быть превращена в стандартной форму перестановки имен переменных и и имена параметров и





Линейный эксцентриситет
Это расстояние от центра до фокуса: .

Эксцентриситет
Эксцентриситет можно выразить как:

предполагая, что эллипс с равными осями ( ) имеет нулевой эксцентриситет и является окружностью.


Полу-латусная прямая кишка
Длина хорды через один очаг, перпендикулярная большой оси, называется latus rectum . Одна его половина - это прямая полупустая кишка . Расчет показывает:


Прямая полу-латусная кишка равна радиусу кривизны в вершинах (см. Кривизну раздела ).

Касательная
Произвольная прямая пересекает эллипс в 0, 1 или 2 точках, соответственно называемых внешней линией , касательной и секущей . Через любую точку эллипса проходит единственная касательная. Касательная в точке эллипса имеет координатное уравнение:




Векторное параметрическое уравнение касательной:
-
 с участием
с участием 
Доказательство:
Позвольте быть точкой на эллипсе и быть уравнением любой строки, содержащей . Подставляя уравнение линии в уравнение эллипса и соблюдая его, получаем:






- Тогда бывают случаи:
-
 Тогда прямая и эллипс имеют только общую точку и являются касательной. Касательное направление имеет перпендикулярный вектор , поэтому касательная линия имеет уравнение для некоторых . Поскольку находится на касательной и эллипсе, получается .
Тогда прямая и эллипс имеют только общую точку и являются касательной. Касательное направление имеет перпендикулярный вектор , поэтому касательная линия имеет уравнение для некоторых . Поскольку находится на касательной и эллипсе, получается .







-
 Тогда прямая имеет вторую точку, общую с эллипсом, и является секущей.
Тогда прямая имеет вторую точку, общую с эллипсом, и является секущей.
Используя (1), можно найти, что это касательный вектор в точке , что доказывает векторное уравнение.


Если и - две точки эллипса такие, что , то точки лежат на двух сопряженных диаметрах (см. Ниже ). (Если эллипс представляет собой круг, а «сопряженный» означает «ортогональный».)




Сдвинутый эллипс
Если стандартный эллипс смещается в центр , его уравнение выглядит следующим образом:


Оси по-прежнему параллельны осям x и y.
Общий эллипс
В аналитической геометрии , эллипс определяется как квадрика : множества точек в декартовой плоскости , что, в невырожденных случаях, удовлетворяют неявное уравнение


предоставлена 
Чтобы отличать вырожденный случай от невырожденного, пусть ∆ - определитель

Тогда эллипс является невырожденным вещественным эллипсом тогда и только тогда, когда C∆ <0. Если C∆ > 0, мы имеем мнимый эллипс, а если ∆ = 0, мы имеем точечный эллипс.
Коэффициенты общего уравнения могут быть получены из известной большой полуоси , малой полуоси , координат центра и угла поворота (угла между положительной горизонтальной осью и большой осью эллипса) по формулам:





Эти выражения могут быть получены из канонического уравнения аффинным преобразованием координат :



И наоборот, параметры канонической формы могут быть получены из коэффициентов общей формы с помощью уравнений:
![{\ displaystyle {\ begin {align} a, b & = {\ frac {- {\ sqrt {2 {\ Big (} AE ^ {2} + CD ^ {2} -BDE + (B ^ {2} -4AC) F {\ Big)} \ left ((A + C) \ pm {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right)}}} {B ^ {2} -4AC} } \\ x _ {\ circ} & = {\ frac {2CD-BE} {B ^ {2} -4AC}} \\ [3pt] y _ {\ circ} & = {\ frac {2AE-BD} {B ^ {2} -4AC}} \\ [3pt] \ theta & = {\ begin {cases} \ arctan \ left ({\ frac {1} {B}} \ left (CA - {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right) \ right) & {\ text {for}} B \ neq 0 \\ 0 & {\ text {for}} B = 0, \ A <C \\ 90 ^ {\ circ} & {\ text {for}} B = 0, \ A> C \\\ end {case}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)
Параметрическое представление

Построение точек на основе параметрического уравнения и интерпретации параметра
t , которое принадлежит де ла Хиру.

Точки эллипса рассчитываются по рациональному представлению с равными разнесенными параметрами ( ).

Стандартное параметрическое представление
Параметрическое представление стандартного эллипса с помощью тригонометрических функций :


Параметр т ( так называемый эксцентрическая аномалия в астрономии) не угол с х Оу, но имеет геометрический смысл из - Филипп де Ла Гир (см Рисунок эллипсы ниже).

Рациональное представление
С помощью подстановки и тригонометрических формул получаем


и рациональное параметрическое уравнение эллипса

покрывающий любую точку эллипса, кроме левой вершины .


Для этой формулы представляет собой правую верхнюю четверть эллипса , двигающийся против часовой стрелки с увеличением Левой вершины является предел![{\ Displaystyle и \ в [0, \, 1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)


Рациональные представления конических сечений обычно используются в автоматизированном проектировании (см. Кривую Безье ).
Касательный наклон как параметр
Параметрическое представление, использующее наклон касательной в точке эллипса, может быть получено из производной стандартного представления :



С помощью тригонометрических формул получаем:

Замена и стандартного представления дает:



Вот наклон касательной в соответствующей точке эллипса, это верхняя и нижняя половина эллипса. Вершины , имеющие вертикальные касательные, представлением не покрываются.




Уравнение касательной в точке имеет вид . Еще неизвестное можно определить, вставив координаты соответствующей точки эллипса :





Это описание касательных эллипса является важным инструментом для определения ортоптики эллипса. Ортоптическая статья содержит другое доказательство, без дифференциального исчисления и тригонометрических формул.
Общий эллипс

Эллипс как аффинное изображение единичной окружности
Другое определение эллипса использует аффинные преобразования :
- Любой эллипс - это аффинное изображение единичной окружности с уравнением .

- Параметрическое представление
Аффинное преобразование евклидовой плоскости имеет вид , где - регулярная матрица (с ненулевым определителем ), - произвольный вектор. Если векторы - столбцы матрицы , единичная окружность , , отображаются на эллипс:








Вот центр и направления двух сопряженных диаметров , в общем, не перпендикулярных.


- Вершины
Четыре вершины эллипса для параметра, определяемого следующим образом:



(Если , то .) Это выводится следующим образом. Касательный вектор в точке :




В параметре вершины касательная перпендикулярна большой / малой осям, поэтому:


Раскрытие и применение тождеств дает уравнение для

- Площадь
Из теоремы Аполлония (см. Ниже) получаем:
площадь эллипса равна


- Полуоси
С сокращениями
формулировки теоремы Аполлония можно записать как:


Решение этой нелинейной системы дает полуоси:



- Неявное представление
Решая параметрическое представление для по правилу Крамера и используя , получаем неявное представление


-
 .
.
Наоборот: если уравнение
-
 с участием
с участием 
эллипса с центром в начале координат, то два вектора

указывают на две сопряженные точки, и инструменты, разработанные выше, применимы.
Пример : для эллипса с уравнением векторы равны

-
 .
.
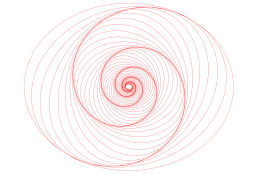
Водовороты: вложенные, масштабированные и повернутые эллипсы. Спираль не рисуется: мы видим ее как
геометрическое место точек, в которых эллипсы особенно близки друг к другу.
- Повернутый стандартный эллипс
Так получается параметрическое представление стандартного эллипса, повернутого на угол :




- Эллипс в космосе
Определение эллипса в этом разделе дает параметрическое представление произвольного эллипса, даже в пространстве, если позволяет быть векторами в пространстве.

Полярные формы
Полярная форма относительно центра

Полярные координаты с центром в центре.
В полярных координатах , с началом в центре эллипса и с угловой координатой, отсчитываемой от большой оси, уравнение эллипса имеет вид


Полярная форма относительно фокуса

Полярные координаты с центром в фокусе.
Если вместо этого мы используем полярные координаты с началом в одном фокусе, а угловая координата по- прежнему отсчитывается от большой оси, уравнение эллипса выглядит следующим образом:


где знак в знаменателе отрицательный, если исходное направление указывает на центр (как показано справа), и положительный, если это направление указывает от центра.

В несколько более общем случае эллипса с одним фокусом в начале координат и другим фокусом по угловой координате , полярная форма имеет вид


Угол в этих формулах называется истинной аномалией точки. В числителе этих формул находится прямая полу-латусная мышца .


Эксцентриситет и свойство директрисы

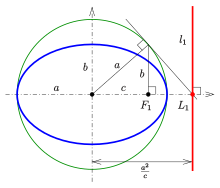
Эллипс: свойство директрисы
Каждая из двух линий, параллельных малой оси и на расстоянии от нее, называется директрисой эллипса (см. Диаграмму).

- Для произвольной точки эллипса отношение расстояния до одного фокуса и соответствующей директрисы (см. Диаграмму) равно эксцентриситету:


Доказательство для пары следует из того, что и удовлетворяют уравнению




Второй случай доказывается аналогично.
Обратное также верно и может использоваться для определения эллипса (аналогично определению параболы):
- Для любой точки (фокуса), любой прямой (директрисы), не проходящей через , и любого действительного числа с эллипсом, это геометрическое место точек, для которых отношение расстояний до точки и до прямой равно:







Расширение до , являющееся эксцентриситетом круга, не допускается в этом контексте в евклидовой плоскости. Однако можно рассматривать директрису круга как бесконечно удаленную линию (с радиусом круга) в проективной плоскости .


(Выбор дает параболу, а если - гиперболу.)



Карандаш из конусов с общей вершиной и общей полурешеткой прямой кишки
- Доказательство
Пусть , и предположим, является точкой на кривой. Директриса имеет уравнение . При соотношение дает уравнения






-
 а также
а также 
Замена дает


Это уравнение эллипса ( ), параболы ( ) или гиперболы ( ). Все эти невырожденные коники имеют общее начало в виде вершины (см. Диаграмму).



Если ввести новые параметры так, чтобы , а затем приведенное выше уравнение принимает вид




который представляет собой уравнение эллипса с центром , осью x как большой осью и большой / малой полуосью .


- Построение директрисы
Поскольку точка директрисы (см. Диаграмму) и фокус инвертированы по отношению к инверсии окружности в окружности (на диаграмме зеленый). Следовательно, его можно построить, как показано на схеме. Направляющая - это перпендикуляр к главной оси в точке .








- Общий эллипс
Если фокус - и направляющая , получаем уравнение



(В правой части уравнения для вычисления расстояния используется нормальная форма линии Гессе .)

Свойство отражения от фокуса к фокусу

Эллипс: касательная делит пополам дополнительный угол угла между линиями к фокусам.

Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус.
Эллипс обладает следующим свойством:
- Нормаль в точке делит угол между линиями пополам .


- Доказательство
Поскольку касательная перпендикулярна нормали, утверждение верно и для касательной и дополнительного угла между линиями к фокусам (см. Диаграмму).
Пусть будет точка на линии с расстоянием до фокуса , это большая полуось эллипса. Пусть линия будет биссектрисой дополнительного угла к углу между прямыми . Чтобы доказать, что это касательная линия в точке , проверяется, что любая точка на прямой, отличная от, не может находиться на эллипсе. Следовательно, имеет только общую точку с эллипсом и, следовательно, является касательной в точке .















Из диаграммы и неравенства треугольника один признает , что имеет место, что означает: . Равенство истинно из теоремы о биссектрисе угла, потому что и . Но если это точка эллипса, сумма должна быть .







- заявка
Лучи из одного фокуса отражаются эллипсом во второй фокус. Это свойство имеет оптические и акустические приложения, аналогичные отражательной способности параболы (см. Галерею шепота ).
Сопряженные диаметры
Определение сопряженных диаметров

Ортогональные диаметры окружности с квадратом касательных, серединами параллельных хорд и аффинным изображением, которое представляет собой эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд.
Круг обладает следующим свойством:
- Середины параллельных хорд лежат на диаметре.
Аффинное преобразование сохраняет параллельность и середины отрезков прямых, поэтому это свойство верно для любого эллипса. (Обратите внимание, что параллельные хорды и диаметр больше не ортогональны.)
- Определение
Два диаметра эллипса сопряжены, если середины хорд, параллельные друг другу, лежат на


Из диаграммы можно найти:
- Два диаметра эллипса сопряжены, если касательные в точках и параллельны им .




Сопряженные диаметры в эллипсе обобщают ортогональные диаметры в окружности.
В параметрическом уравнении для общего эллипса, приведенном выше,

любая пара точек принадлежит диаметру, а пара принадлежит его сопряженному диаметру.


Теорема Аполлония о сопряженных диаметрах

Для альтернативной формулы площади
Для эллипса с полуосями верно следующее:

- Пусть и - половинки двух сопряженных диаметров (см. Диаграмму), тогда


-
 .
.
- Треугольника со сторонами (см схему) имеет площадь постоянной , которая может быть выражено , тоже. - высота точки и угол между половинными диаметрами. Следовательно, площадь эллипса (см. Свойства метрики раздела ) может быть записана как .








- Параллелограмм касательных, примыкающих к заданным сопряженным диаметрам, имеет

- Доказательство
Пусть эллипс имеет каноническую форму с параметрическим уравнением
-
 .
.
Две точки находятся на сопряженных диаметрах (см. Предыдущий раздел). Из тригонометрических формул получаем и



Площадь треугольника , порожденный IS


а из диаграммы видно, что площадь параллелограмма в 8 раз больше площади . Следовательно


Ортогональные касательные

Эллипс с его ортоптическими
Для эллипса точки пересечения ортогональных касательных лежат на окружности .


Этот круг называется ортоптическим или направляющим кругом эллипса (не путать с круговой направляющей, определенной выше).
Рисование эллипсов

Центральная проекция кругов (ворот)
Эллипсы появляются в начертательной геометрии как изображения (параллельная или центральная проекция) кругов. Существуют различные инструменты для рисования эллипса. Компьютеры предоставляют самый быстрый и точный метод рисования эллипса. Однако технические инструменты ( эллипсографы ) для рисования эллипса без использования компьютера существуют. Принцип эллипсографов был известен греческим математикам, таким как Архимед и Проклос .
Если эллипсограф недоступен, можно нарисовать эллипс, аппроксимируя его четырьмя соприкасающимися окружностями в вершинах .
Для любого метода, описанного ниже, необходимо знание осей и полуосей (или, что эквивалентно: фокусов и большой полуоси). Если это предположение не выполняется, необходимо знать как минимум два сопряженных диаметра. С помощью конструкции Ритца можно восстановить оси и полуоси.
Конструкция точки де Ла Хира
Следующее построение отдельных точек эллипса принадлежит де Ла Иру . Он основан на стандартном параметрическом представлении эллипса:

- Нарисуйте два круга с центром в центре эллипса с радиусами и осями эллипса.

- Проведите линию через центр , которая пересекает два круга в точках и соответственно.


- Нарисуйте линию через который параллелен оси малой и линии через которые параллельно главной оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).


- Повторите шаги (2) и (3) с разными линиями через центр.
Булавочный метод
Характеристика эллипса как геометрического места точек, так что сумма расстояний до фокусов постоянна, приводит к способу рисования эллипса с использованием двух булавок , длины веревки и карандаша. В этом методе булавки вставляются в бумагу в двух точках, которые становятся фокусами эллипса. На каждом конце к двум булавкам привязывается веревка; его длина после завязывания составляет . Затем кончик карандаша образует эллипс, если его перемещать, сохраняя натянутую нить. Используя два колышка и веревку, садовники используют эту процедуру, чтобы очертить эллиптическую клумбу - таким образом, она называется эллипсом садовника .

Аналогичный метод для рисования конфокальных эллипсов с замкнутой струной из - за ирландским епископ Чарльз Грейвза .
Методы бумажной ленты
Два следующих метода полагаются на параметрическое представление (см. Раздел « Параметрическое представление» выше):

Технически это представление можно смоделировать двумя простыми способами. В обоих случаях необходимо знать центр, оси и полуоси .

- Способ 1
Первый метод начинается с
- полоска бумаги длины .

Точка пересечения полуосей отмечена значком . Если полоса скользит обоими концами по осям желаемого эллипса, то точка отслеживает эллипс. Для доказательства показано, что точка имеет параметрическое представление , где параметр - угол наклона бумажной полосы.





Техническая реализация движения бумажной полоски может быть достигнута парой Туси (см. Анимацию). Устройство способно нарисовать любой эллипс с фиксированной суммой , равной радиусу большого круга. Это ограничение может быть недостатком в реальной жизни. Более гибким является второй метод бумажной ленты.

Построение эллипса: метод бумажной ленты 1
Эллипсы с парой Туси. Два примера: красный и голубой.
Вариант способа 1 бумажной полосы использует наблюдение, что средняя точка бумажной полосы движется по окружности с центром (эллипса) и радиусом . Следовательно, бумажную ленту можно разрезать на части , снова соединить стыком в точке и зафиксировать скользящий конец в центре (см. Диаграмму). После этой операции движение неизменной половины полоски бумаги не меняется. Этот вариант требует только одного скользящего башмака.







Вариант метода бумажной ленты 1
Анимация вариации метода бумажной ленты 1

Построение эллипса: метод бумажной полосы 2
- Способ 2
Второй способ начинается с
- полоска бумаги длины .

Один отмечает точку, которая разделяет полосу на две части длины и . Полоса размещается на осях, как показано на схеме. Затем свободный конец полоски очерчивает эллипс, при этом полоска перемещается. Для доказательства следует признать, что точка отслеживания может быть описана параметрически с помощью , где параметр - угол наклона бумажной полосы.




Этот метод является основой для нескольких эллипсографов (см. Раздел ниже).
Подобно варианту способа 1 с полосой бумаги, вариант способа 2 с полосой бумаги может быть реализован (см. Диаграмму) путем разрезания части между осями пополам.
Вариант метода бумажной ленты 2
Большинство инструментов для рисования эллипсографов основаны на втором методе бумажной ленты.

Аппроксимация эллипса соприкасающимися окружностями
Аппроксимация соприкасающимися кругами
Из метрических свойств, представленных ниже, можно получить:
- Радиус кривизны в вершинах :


- Радиус кривизны в совпадении вершин равен:


На схеме показан простой способ найти центры кривизны в вершине и совершине соответственно:



- отметьте вспомогательную точку и проведите отрезок линии


- проведите линию , которая перпендикулярна линии


- точки пересечения этой линии с осями являются центрами соприкасающихся окружностей.
(доказательство: простой расчет.)
Центры остальных вершин находятся по симметрии.
С помощью французской кривой проводят кривую, которая имеет плавный контакт с соприкасающимися кругами .
Поколение Штайнера

Эллипс: поколение Штайнера

Эллипс: поколение Штайнера
Следующий метод построения отдельных точек эллипса основан на генерации Штейнера конического сечения :
- Принимая во внимание два карандашей линий в двух точках (все строки , содержащие и , соответственно) и проективное , но не перспективное отображение из на , то точки пересечения соответствующих линий образуют невырожденную проективное коническое сечение.







Для создания точек эллипса используются карандаши в вершинах . Позвольте быть верхней совершиной эллипса и .




 это центр прямоугольника . Сторона прямоугольника делится на n линейных сегментов с равным интервалом, и это деление проецируется параллельно диагонали в качестве направления на линейный сегмент и назначает деление, как показано на диаграмме. Параллельная проекция вместе с реверсом ориентации является частью проективного отображения между пучками в и необходимо. Точки пересечения любых двух связанных прямых и являются точками однозначно определенного эллипса. С помощью точек можно определить точки второй четверти эллипса. Аналогично получают точки нижней половины эллипса.
это центр прямоугольника . Сторона прямоугольника делится на n линейных сегментов с равным интервалом, и это деление проецируется параллельно диагонали в качестве направления на линейный сегмент и назначает деление, как показано на диаграмме. Параллельная проекция вместе с реверсом ориентации является частью проективного отображения между пучками в и необходимо. Точки пересечения любых двух связанных прямых и являются точками однозначно определенного эллипса. С помощью точек можно определить точки второй четверти эллипса. Аналогично получают точки нижней половины эллипса.









Генерация Штейнера также может быть определена для гипербол и парабол. Его иногда называют методом параллелограмма, потому что можно использовать другие точки, а не вершины, который начинается с параллелограмма вместо прямоугольника.
Как гипотрохоид
Эллипс - это частный случай гипотрохоиды, когда , как показано на соседнем изображении. Частный случай движущегося круга с радиусом внутри круга с радиусом называется парой Туси .



Вписанные углы и трехточечная форма
Круги

Круг: теорема о вписанном угле
Круг с уравнением однозначно определяется тремя точками, а не прямой. Простой способ определения параметров использует теорему о вписанном угле для окружностей:



- Для четырех точек (см. Диаграмму) верно следующее утверждение:

- Четыре точки находятся на окружности тогда и только тогда, когда углы равны и равны.


Обычно вписанные углы измеряют градусом или радианом θ, но здесь более удобно следующее измерение:
- Чтобы измерить угол между двумя линиями с помощью уравнений, используется частное:


Теорема о вписанном угле для окружностей
Для четырех точек, а не трех из них на прямой, имеем следующее (см. Диаграмму):

- Четыре точки находятся на окружности, если и только если углы равны и равны. С точки зрения измерения угла, приведенного выше, это означает:



Сначала такт доступен только для хорд, не параллельных оси Y, но окончательная формула работает для любого аккорда.
Трехточечная форма уравнения окружности
- Как следствие, получаем уравнение для окружности, определяемой тремя неколлинеарными точками :


Например, для трехточечного уравнения это:

-
 , который можно изменить на
, который можно изменить на 
Используя векторы, скалярные произведения и детерминанты, эту формулу можно упорядочить более четко, позволяя :


Центр круга удовлетворяет:


Радиус - это расстояние между любой из трех точек и центром.

Эллипсы
В этом разделе мы рассматриваем семейство эллипсов, определяемое уравнениями с фиксированным эксцентриситетом . Удобно использовать параметр:



и записать уравнение эллипса как:

где q фиксировано и изменяется в зависимости от действительных чисел. (Такие эллипсы имеют оси, параллельные осям координат: если большая ось параллельна оси x ; если она параллельна оси y .)




Теорема о вписанном угле для эллипса
Подобно кругу, такой эллипс определяется тремя точками, расположенными не на одной прямой.
Для этого семейства эллипсов вводится следующая q-аналоговая угловая мера, которая не является функцией обычной угловой меры θ :
- Чтобы измерить угол между двумя линиями с помощью уравнений, используется частное:


Теорема о вписанном угле для эллипсов
- Учитывая четыре точки , нет трех из них на линии (см. Диаграмму).

- Четыре точки находятся на эллипсе с уравнением тогда и только тогда, когда углы равны и равны в смысле измерения выше, то есть если




Сначала такт доступен только для хорд, которые не параллельны оси ординат. Но окончательная формула работает для любого аккорда. Доказательство следует из прямого вычисления. Для направления доказательства, учитывая, что точки находятся на эллипсе, можно предположить, что центр эллипса является началом координат.
Трехточечная форма уравнения эллипса
- Как следствие, получаем уравнение для эллипса, определяемого тремя неколлинеарными точками :


Например, для и получается трехточечная форма


-
 и после преобразования
и после преобразования 
Аналогично случаю круга уравнение можно более четко записать с помощью векторов:

где модифицированный скалярный продукт

Полярно-полярное отношение

Эллипс: полярно-полярное отношение
Любой эллипс можно описать в подходящей системе координат уравнением . Уравнение касательной в точке эллипса: Если позволить точке быть произвольной точкой, отличной от начала координат, то




- точка отображается на линию , а не через центр эллипса.


Это отношение между точками и линиями является взаимно однозначным .
В обратной функции карты
- линия на точку и


- линия на точку


Такое отношение между точками и линиями, образованными коникой, называется полярно-полярным отношением или полярностью . Полюс - это точка; полярная линия.
Расчетным путем можно подтвердить следующие свойства полярно-полярной связи эллипса:
- Для точки (полюса) на эллипсе полярная точка является касательной в этой точке (см. Диаграмму:) .

- Для полюса вне эллипса точки пересечения его поляры с эллипсом являются точками касания двух проходящих касательных (см. Диаграмму:) .



- Для точки внутри эллипса полярная точка не имеет общей точки с эллипсом (см. Диаграмму:) .

- Точка пересечения двух поляр - это полюс линии, проходящей через их полюса.
- Фокусы и , соответственно, и направляющие, и , соответственно, принадлежат парам полюса и полюса. Поскольку они являются даже полярными парами по отношению к окружности , направляющие могут быть построены с помощью циркуля и линейки (см. Инверсивная геометрия ).





Отношения между полюсами и полюсами существуют также для гипербол и парабол.
Метрические свойства
Все приведенные ниже метрические свойства относятся к эллипсу с уравнением
-
 |
|
( 1 )
|
за исключением участка, ограниченного наклонным эллипсом, где будет дана обобщенная форма уравнения ( 1 ).
Площадь
Площадь обнесена эллипса:

-
 |
|
( 2 )
|
где и - длины большой и малой полуосей соответственно. Формула площади интуитивно понятна: начните с круга радиуса (т.е. его площадь ) и растяните его на коэффициент, чтобы получился эллипс. Это масштабирует площадь с тем же коэффициентом: также легко строго доказать формулу площади, используя интегрирование следующим образом. Уравнение ( 1 ) можно переписать как Для этой кривой находится верхняя половина эллипса. Таким образом, удвоенный интеграл по интервалу будет площадью эллипса:








![{\ Displaystyle х \ в [-а, а],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a, a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)

Второй интеграл - это площадь круга радиуса, то есть So



Эллипс, неявно определяемый площадью has

Площадь также может быть выражена в терминах эксцентриситета и длины большой полуоси как (полученная путем решения для выравнивания с последующим вычислением малой полуоси).

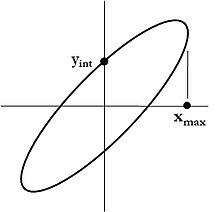
Площадь, ограниченная наклонным эллипсом, равна .

До сих пор мы имели дело с стоячими эллипсов, чьи большие и малые оси которых параллельны и осей. Однако для некоторых приложений требуются наклонные эллипсы. Например, в оптике пучка заряженных частиц замкнутая область прямолинейного или наклонного эллипса является важным свойством пучка, его эмиттансом . В этом случае все еще применима простая формула, а именно


-
 |
|
( 3 )
|
где , - точки пересечения , - максимальные значения. Это непосредственно следует из теоремы Аполлонио .




Длина окружности

Эллипсы с одинаковой окружностью
Окружность эллипса равна:


где снова - длина большой полуоси, - эксцентриситет, а функция - полный эллиптический интеграл второго рода ,




что вообще не является элементарной функцией .
Окружность эллипса может быть оценена с использованием среднего арифметико-геометрического Гаусса ; это квадратично сходящийся итерационный метод.

Точная бесконечная серия :
![{\ displaystyle {\ begin {align} C & = 2 \ pi a \ left [{1- \ left ({\ frac {1} {2}} \ right) ^ {2} e ^ {2} - \ left ( {\ frac {1 \ cdot 3} {2 \ cdot 4}} \ right) ^ {2} {\ frac {e ^ {4}} {3}} - \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) ^ {2} {\ frac {e ^ {6}} {5}} - \ cdots} \ right] \\ & = 2 \ pi a \ left [1- \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}} \ right] \\ & = - 2 \ pi a \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}}, \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
где - двойной факториал (расширенный до отрицательных нечетных целых чисел рекуррентным соотношением для ). Этот ряд сходится, но, расширив его с точки зрения Джеймса Айвори и Бесселя, получили выражение, которое сходится гораздо быстрее:




![{\ displaystyle {\ begin {align} C & = \ pi (a + b) \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ { n} n!}} \ right) ^ {2} h ^ {n} \\ & = \ pi (a + b) \ left [1 + {\ frac {h} {4}} + \ sum _ {n = 2} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ Right) ^ {2} h ^ {n} \ right] \\ & = \ pi (a + b) \ left [1+ \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {2 ^ {n} n! }} \ right) ^ {2} {\ frac {h ^ {n}} {(2n-1) ^ {2}}} \ right]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
Шриниваса Рамануджан дает два близких приближения для окружности в § 16 «Модульных уравнений и приближения к »; они есть

![{\ Displaystyle С \ приблизительно \ pi {\ biggl [} 3 (a + b) - {\ sqrt {(3a + b) (a + 3b)}} {\ biggr]} = \ pi {\ biggl [} 3 (a + b) - {\ sqrt {10ab + 3 \ left (a ^ {2} + b ^ {2} \ right)}} {\ biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)
а также

Погрешности этих приближений, полученных эмпирическим путем, имеют порядок и соответственно.


Длина дуги
В более общем смысле, длина дуги части окружности как функция от прилегающего угла (или x -координат любых двух точек в верхней половине эллипса) задается неполным эллиптическим интегралом . Верхняя половина эллипса параметризована

Тогда длина дуги от до составляет:




Это эквивалентно
![{\ Displaystyle s = -b \ left [E \ left (z \; {\ Biggl |} \; 1 - {\ frac {a ^ {2}} {b ^ {2}}} \ right) \ right] _ {\ arccos {\ frac {x_ {1}} {a}}} ^ {\ arccos {\ frac {x_ {2}} {a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)
где - неполный эллиптический интеграл второго рода с параметром

Обратная функция , угол , образуемый в зависимости от длины дуги, задаются некоторой эллиптической функцией .
Некоторые нижние и верхние границы окружности канонического эллипса с равными



Здесь верхняя граница - это окружность описанной концентрической окружности, проходящей через концы большой оси эллипса, а нижняя граница - это периметр вписанного ромба с вершинами на концах большой и малой осей.


Кривизна
Кривизны задается радиусом кривизны в точке :



Радиус кривизны в двух вершинах и центрах кривизны:


Радиус кривизны в двух совпадающих вершинах и в центрах кривизны:


В геометрии треугольника
Эллипсы появляются в геометрии треугольника как
-
Эллипс Штейнера : эллипс, проходящий через вершины треугольника с центром в центроиде,
-
inellipses : эллипсы, которые касаются сторон треугольника. Особые случаи являются inellipse Steiner и inellipse Mandart .
Как плоские сечения квадрик
Эллипсы выглядят как плоские секции следующих квадрик :
Гиперболоид из двух листов
Приложения
Физика
Эллиптические отражатели и акустика
Если поверхность воды нарушается в одном фокусе эллиптического резервуара с водой, круговые волны этого возмущения после отражения от стен сходятся одновременно в одной точке: во втором фокусе . Это следствие того, что общая длина пути одинакова на любом пути отскока от стен между двумя фокусами.
Точно так же, если источник света расположен в одном фокусе эллиптического зеркала , все световые лучи в плоскости эллипса отражаются во второй фокус. Так как никакая другая гладкая кривая не обладает таким свойством, ее можно использовать в качестве альтернативного определения эллипса. (В частном случае круга с источником в центре весь свет будет отражаться обратно в центр.) Если эллипс вращается вдоль его большой оси, чтобы получить эллипсоидальное зеркало (в частности, вытянутый сфероид ), это свойство сохраняется. для всех лучей, выходящих из источника. В качестве альтернативы можно использовать цилиндрическое зеркало с эллиптическим поперечным сечением для фокусировки света от линейной люминесцентной лампы вдоль линии бумаги; такие зеркала используются в некоторых сканерах документов .
Звуковые волны отражаются аналогичным образом, поэтому в большой эллиптической комнате человек, стоящий в одном фокусе, может замечательно хорошо слышать человека, стоящего в другом фокусе. Эффект еще более заметен под сводчатой крышей, имеющей форму вытянутого сфероида. Такое помещение называется камерой шепота . Тот же эффект можно продемонстрировать с двумя отражателями, имеющими форму торцевых крышек такого сфероида, расположенными напротив друг друга на определенном расстоянии. Примерами являются Национальный зал скульптур в Капитолии Соединенных Штатов (где, как говорят, Джон Куинси Адамс использовал эту собственность для подслушивания политических вопросов); мормонов Скиния на Храмовой площади в Солт - Лейк - Сити , штат Юта ; на выставке звука в Музее науки и промышленности в Чикаго ; перед Университетом Иллинойса в аудитории Урбана-Шампейн Феллингер; а также в боковой комнате дворца Карла V в Альгамбре .
Планетарные орбиты
В 17 веке Иоганнес Кеплер в своем первом законе движения планет обнаружил, что орбиты, по которым планеты движутся вокруг Солнца, представляют собой эллипсы с Солнцем [приблизительно] в одном фокусе . Позже Исаак Ньютон объяснил это следствием своего закона всемирного тяготения .
В более общем плане, в гравитационной задаче двух тел, если два тела связаны друг с другом (то есть, полная энергия отрицательна), их орбиты представляют собой аналогичные эллипсы, причем общий барицентр является одним из фокусов каждого эллипса. Другой фокус любого эллипса не имеет известного физического значения. Орбита одного тела в системе отсчета другого тела также является эллипсом с другим телом в том же фокусе.
Кеплеровские эллиптические орбиты являются результатом любой радиально направленной силы притяжения, сила которой обратно пропорциональна квадрату расстояния. Таким образом, в принципе движение двух противоположно заряженных частиц в пустом пространстве также было бы эллипсом. (Однако этот вывод игнорирует потери из-за электромагнитного излучения и квантовых эффектов , которые становятся значительными, когда частицы движутся с высокой скоростью.)
Для эллиптических орбит полезные соотношения, включающие эксцентриситет, следующие:


куда
-
 это радиус в апоапсисе (самое дальнее расстояние)
это радиус в апоапсисе (самое дальнее расстояние)
-
 радиус в перицентре (ближайшее расстояние)
радиус в перицентре (ближайшее расстояние)
-
 длина большой полуоси
длина большой полуоси
Кроме того , с точки зрения и , то большая полуось их среднее арифметическое , ось полу-минор является их среднее геометрическое , и полу-Латус прямая кишка является их гармоническое среднее . Другими словами,





-
![{\ displaystyle {\ begin {align} a & = {\ frac {r_ {a} + r_ {p}} {2}} \\ [2pt] b & = {\ sqrt {r_ {a} r_ {p}}} \\ [2pt] \ ell & = {\ frac {2} {{\ frac {1} {r_ {a}}} + {\ frac {1} {r_ {p}}}}} = {\ frac { 2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271) .
.
Гармонические осцилляторы
Общее решение для гармонического осциллятора в двух или более измерениях также является эллипсом. Так обстоит дело, например, с длинным маятником, который может свободно двигаться в двух измерениях; массы, прикрепленной к неподвижной точке совершенно упругой пружиной ; или любого объекта, который движется под действием силы притяжения, которая прямо пропорциональна его расстоянию от фиксированного аттрактора. Однако, в отличие от кеплеровских орбит, эти «гармонические орбиты» имеют центр притяжения в геометрическом центре эллипса и имеют довольно простые уравнения движения.
Визуализация фаз
В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа . Если отображение фигуры Лиссажу представляет собой эллипс, а не прямую линию, два сигнала не совпадают по фазе.
Эллиптические шестерни
Две некруглые шестерни с одинаковым эллиптическим контуром, каждая из которых вращается вокруг одного фокуса и расположена под правильным углом, плавно вращаются, сохраняя постоянный контакт. В качестве альтернативы, они могут быть соединены звеньевой цепью или зубчатым ремнем , или в случае велосипеда главная передняя звезда может быть эллиптической или яйцевидной формы, похожей на эллипс. Такие эллиптические шестерни могут использоваться в механическом оборудовании для создания переменной угловой скорости или крутящего момента за счет постоянного вращения ведущей оси или, в случае велосипеда, для обеспечения переменной скорости вращения кривошипа с обратно изменяющимся механическим преимуществом .
Эллиптические велосипедные шестерни облегчают соскальзывание цепи с зубца при переключении передач.
Пример применения передач будет представлять собой устройство , что ветры нить на конической бобины на прядильной машине. Шпулька должна наматываться быстрее, когда нить находится рядом с вершиной, чем когда она находится рядом с основанием.
Оптика
- В материале, который является оптически анизотропным ( двулучепреломляющим ), показатель преломления зависит от направления света. Зависимость может быть описана эллипсоидом индексов . (Если материал оптически изотропен , этот эллипсоид представляет собой сферу.)
- В lamp- накачки твердотельных лазеров, эллиптические цилиндрическая форме отражатели были использованы для прямого света от лампы накачки (коаксиальной с фокусной осью эллипса один) к активной среде стержню (коаксиальному со вторым фокальной оси).
- В лазерно-плазменных источниках EUV- света, используемых в литографии микрочипов , EUV-свет генерируется плазмой, расположенной в первичном фокусе эллипсоидного зеркала, и собирается во вторичном фокусе на входе литографической машины.
Статистика и финансы
В статистике , двумерный случайный вектор является совместно эллиптический распределен , если его изо-плотность контуры локусов равных значений плотности функции-эллипсы. Эта концепция распространяется на произвольное число элементов случайного вектора, и в этом случае в общем случае контуры изоплотности являются эллипсоидами. Особый случай - многомерное нормальное распределение . Эллиптические распределения важны в финансах, потому что, если нормы прибыли на активы совместно распределены эллиптически, тогда все портфели можно полностью охарактеризовать их средним значением и дисперсией, то есть любые два портфеля с одинаковым средним значением и дисперсией доходности портфеля имеют идентичные распределения портфеля. возвращение.

Компьютерная графика
Рисование эллипса как графического примитива является обычным делом в стандартных библиотеках отображения, таких как MacIntosh QuickDraw API и Direct2D в Windows. Джек Брезенхэм из IBM наиболее известен изобретением примитивов 2D-рисования, в том числе рисования линий и окружностей, с использованием только быстрых целочисленных операций, таких как сложение и переход по биту переноса. В 1967 году MLV Pitteway расширил алгоритм Брезенхэма для линий на коники. Еще одно эффективное обобщение для рисования эллипсов было изобретено в 1984 году Джерри Ван Акеном.
В 1970 году Дэнни Коэн представил на конференции «Компьютерная графика 1970» в Англии линейный алгоритм для рисования эллипсов и окружностей. В 1971 г. Л. Б. Смит опубликовал аналогичные алгоритмы для всех конических сечений и доказал их хорошие свойства. Этим алгоритмам требуется всего несколько умножений и сложений для вычисления каждого вектора.
В компьютерной графике полезно использовать параметрическую формулировку, потому что плотность точек максимальна там, где больше всего кривизны. Таким образом, изменение наклона между каждой последовательной точкой невелико, что снижает кажущуюся «неровность» приближения.
- Рисование контурами Безье
Составные кривые Безье также могут использоваться для рисования эллипса с достаточной точностью, поскольку любой эллипс может быть истолкован как аффинное преобразование круга. Сплайновые методы, используемые для рисования круга, могут использоваться для рисования эллипса, поскольку составляющие кривые Безье ведут себя соответствующим образом при таких преобразованиях.
Теория оптимизации
Иногда бывает полезно найти минимальный ограничивающий эллипс на множестве точек. Для решения этой проблемы весьма полезен метод эллипсоида .
Смотрите также
-
Декартов овал , обобщение эллипса
- Циркумконический и инконический
- Расстояние максимального сближения эллипсов
- Подгонка эллипса
-
Эллиптические координаты , ортогональная система координат, основанная на семействах эллипсов и гипербол.
- Эллиптическое уравнение в частных производных
-
Эллиптическое распределение в статистике
- Эллиптический купол
- Геодезические на эллипсоиде
- Большой эллипс
- Законы движения планет Кеплера
-
n -эллипс , обобщение эллипса для n фокусов
- Овал
-
Сфероид , эллипсоид, полученный вращением эллипса вокруг его большой или малой оси.
-
Стадион (геометрия) , двумерная геометрическая фигура, состоящая из прямоугольника с полукругами на паре противоположных сторон.
-
Окружность Штейнера , уникальный эллипс, описывающий треугольник и разделяющий его центр тяжести
-
Суперэллипс , обобщение эллипса, который может выглядеть более прямоугольным или более «заостренным».
-
Истинная , эксцентричная и средняя аномалия
Примечания
использованная литература
-
Безант, WH (1907). «Глава III. Эллипс» . Конические сечения . Лондон: Джордж Белл и сыновья. п. 50.
-
Кокстер, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк: Вили. С. 115–9 .
-
Месерв, Брюс Э. (1983) [1959], Основные концепции геометрии , Dover Publications, ISBN 978-0-486-63415-9
-
Миллер, Чарльз Д .; Lial, Margaret L .; Шнайдер, Дэвид I. (1990). Основы студенческой алгебры (3-е изд.). Скотт Форесман / Литтл. п. 381 . ISBN 978-0-673-38638-0.
-
Protter, Murray H .; Морри, Чарльз Б. Младший (1970), Колледж по исчислению с аналитической геометрией (2-е изд.), Чтение: Addison-Wesley , LCCN 76087042
внешние ссылки
-
 Цитаты, связанные с Ellipse на Wikiquote
Цитаты, связанные с Ellipse на Wikiquote
-
 СМИ, связанные с эллипсами на Викискладе?
СМИ, связанные с эллипсами на Викискладе?
-
эллипс в PlanetMath .
- Вайсштейн, Эрик В. «Эллипс» . MathWorld .
- Вайсштейн, Эрик В. «Эллипс как частный случай гипотрохоидов» . MathWorld .
-
Вывод Аполлонием эллипса при сходимости
-
Форма и история эллипса в Вашингтоне, округ Колумбия , Кларк Кимберлинг
- Калькулятор длины окружности эллипса
- Коллекция демонстраций анимированных эллипсов
-
Иванов, А.Б. (2001) [1994], "Эллипс" , Математическая энциклопедия , EMS Press
- Trammel по Frans van Schooten



 Цитаты, связанные с Ellipse на Wikiquote
Цитаты, связанные с Ellipse на Wikiquote СМИ, связанные с эллипсами на Викискладе?
СМИ, связанные с эллипсами на Викискладе?






















































































![{\ displaystyle {\ begin {align} a, b & = {\ frac {- {\ sqrt {2 {\ Big (} AE ^ {2} + CD ^ {2} -BDE + (B ^ {2} -4AC) F {\ Big)} \ left ((A + C) \ pm {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right)}}} {B ^ {2} -4AC} } \\ x _ {\ circ} & = {\ frac {2CD-BE} {B ^ {2} -4AC}} \\ [3pt] y _ {\ circ} & = {\ frac {2AE-BD} {B ^ {2} -4AC}} \\ [3pt] \ theta & = {\ begin {cases} \ arctan \ left ({\ frac {1} {B}} \ left (CA - {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right) \ right) & {\ text {for}} B \ neq 0 \\ 0 & {\ text {for}} B = 0, \ A <C \\ 90 ^ {\ circ} & {\ text {for}} B = 0, \ A> C \\\ end {case}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)









![{\ Displaystyle и \ в [0, \, 1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)

































































































































































































































































![{\ Displaystyle х \ в [-а, а],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a, a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)




















![{\ displaystyle {\ begin {align} C & = 2 \ pi a \ left [{1- \ left ({\ frac {1} {2}} \ right) ^ {2} e ^ {2} - \ left ( {\ frac {1 \ cdot 3} {2 \ cdot 4}} \ right) ^ {2} {\ frac {e ^ {4}} {3}} - \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) ^ {2} {\ frac {e ^ {6}} {5}} - \ cdots} \ right] \\ & = 2 \ pi a \ left [1- \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}} \ right] \\ & = - 2 \ pi a \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}}, \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)




![{\ displaystyle {\ begin {align} C & = \ pi (a + b) \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ { n} n!}} \ right) ^ {2} h ^ {n} \\ & = \ pi (a + b) \ left [1 + {\ frac {h} {4}} + \ sum _ {n = 2} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ Right) ^ {2} h ^ {n} \ right] \\ & = \ pi (a + b) \ left [1+ \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {2 ^ {n} n! }} \ right) ^ {2} {\ frac {h ^ {n}} {(2n-1) ^ {2}}} \ right]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{\ Displaystyle С \ приблизительно \ pi {\ biggl [} 3 (a + b) - {\ sqrt {(3a + b) (a + 3b)}} {\ biggr]} = \ pi {\ biggl [} 3 (a + b) - {\ sqrt {10ab + 3 \ left (a ^ {2} + b ^ {2} \ right)}} {\ biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)








![{\ Displaystyle s = -b \ left [E \ left (z \; {\ Biggl |} \; 1 - {\ frac {a ^ {2}} {b ^ {2}}} \ right) \ right] _ {\ arccos {\ frac {x_ {1}} {a}}} ^ {\ arccos {\ frac {x_ {2}} {a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)




















![{\ displaystyle {\ begin {align} a & = {\ frac {r_ {a} + r_ {p}} {2}} \\ [2pt] b & = {\ sqrt {r_ {a} r_ {p}}} \\ [2pt] \ ell & = {\ frac {2} {{\ frac {1} {r_ {a}}} + {\ frac {1} {r_ {p}}}}} = {\ frac { 2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271)
