1-2 + 3-4 + ⋯ - 1 − 2 + 3 − 4 + ⋯

Первые 15 000 частичных сумм 0 + 1 - 2 + 3 - 4 + ... График расположен с положительными целыми числами справа и отрицательными целыми числами слева.

В математике , 1 - 2 + 3 - 4 + ··· представляет собой бесконечный ряд , члены которого являются последовательными положительными целыми числами , при знакопеременных . Используя обозначение суммирования сигма, сумма первых m членов ряда может быть выражена как

{\ displaystyle \ sum _ {n = 1} ^ {m} n (-1) ^ {n-1}.}

В серии бесконечная расходится , а это означает , что его последовательность частичных сумм , (1, -1, 2, -2, ...) , не склонна к любому конечному пределу . Тем не менее, в середине 18 века Леонард Эйлер написал то, что, по его признанию, было парадоксальным уравнением :

{\ displaystyle 1-2 + 3-4 + \ cdots = {\ frac {1} {4}}.}

Строгое объяснение этого уравнения не будет прибывать до гораздо позже. Начиная с 1890 года Эрнесто Чезаро , Эмиль Борель и другие исследовали четко определенные методы приписывания обобщенных сумм расходящимся рядам, включая новые интерпретации попыток Эйлера. Многие из этих методов суммирования легко присваивают 1 - 2 + 3 - 4 + ... "значение"1/4. Суммирование Чезаро - один из немногих методов, которые не суммируют 1 - 2 + 3 - 4 + ... , поэтому ряд является примером, где требуется более сильный метод, такой как суммирование Абеля .

Серия 1 - 2 + 3 - 4 + ... тесно связана с серией Гранди 1 - 1 + 1 - 1 + ... . Эйлер рассматривал эти два случая как частные случаи более общей последовательности 1-2 ⁿ + 3 ⁿ - 4 ⁿ + ... , где n = 1 и n = 0 соответственно. Это направление исследований расширило его работу над проблемой Базеля и привело к функциональным уравнениям того, что сейчас известно как эта-функция Дирихле и дзета-функция Римана .

Расхождение

Члены ряда (1, −2, 3, −4, ...) не стремятся к нулю ; поэтому 1 - 2 + 3 - 4 + ... расходится по термину test . Дивергенция также может быть показана непосредственно из определения: бесконечный ряд сходится тогда и только тогда, когда последовательность частичных сумм сходится к пределу , и в этом случае этот предел является значением бесконечного ряда. Частичные суммы 1-2 + 3-4 + ... составляют:

1 ,

1-2 = -1 ,
1-2 + 3 = 2 ,
1-2 + 3-4 = -2 ,
1-2 + 3-4 + 5 = 3 ,
1-2 + 3-4 + 5-6 = −3 ,

...

Последовательность частичных сумм показывает, что ряд не сходится к определенному числу: для любого предложенного предела x существует точка, за которой все последующие частичные суммы лежат за пределами интервала [ x −1, x +1] ), поэтому 1-2 + 3-4 + ... расходится.

Частичные суммы включают каждое целое число ровно один раз даже 0 , если один отсчитывает пустая частичная сумму й тот самый устанавливает счетность множества из целых чисел . ${\ Displaystyle \ mathbb {Z}}$

Эвристика для суммирования

Стабильность и линейность

Поскольку члены 1, −2, 3, −4, 5, −6, ... следуют простому шаблону, рядами 1-2 + 3-4 + ... можно манипулировать, сдвигая и почленно сложение для получения числового значения. Если есть смысл написать s = 1-2 + 3-4 + ... для некоторого обычного числа s , следующие манипуляции приводят к тому, что s = 1 ⁄ 4 :

{\ displaystyle {\ begin {array} {rclllll} 4s & = && (1-2 + 3-4 + \ cdots) & {} + (1-2 + 3-4 + \ cdots) & {} + (1- 2 + 3-4 + \ cdots) & {} + (1-2 + 3-4 + \ cdots) \\ & = && (1-2 + 3-4 + \ cdots) & {} + 1 + (- 2 + 3-4 + 5 + \ cdots) & {} + 1 + (- 2 + 3-4 + 5 + \ cdots) & {} + (1-2) + (3-4 + 5-6 \ cdots ) \\ & = && (1-2 + 3-4 + \ cdots) & {} + 1 + (- 2 + 3-4 + 5 + \ cdots) & {} + 1 + (- 2 + 3-4 +5+ \ cdots) & {} - 1+ (3-4 + 5-6 \ cdots) \\ & = & 1 + & (1-2 + 3-4 + \ cdots) & {} + (- 2+ 3-4 + 5 + \ cdots) & {} + (- 2 + 3-4 + 5 + \ cdots) & {} + (3-4 + 5-6 \ cdots) \\ & = & 1 + [& (1 -2-2 + 3) & {} + (- 2 + 3 + 3-4) & {} + (3-4-4 + 5) & {} + (- 4 + 5 + 5-6) + \ cdots] \\ & = & 1 + [& 0 + 0 + 0 + 0 + \ cdots] \\ 4s & = & 1 \ end {array}}}

Добавление 4 копий 1 - 2 + 3 - 4 + ..., используя только сдвиги и посроченное сложение, дает 1. Левая и правая стороны демонстрируют по две копии 1 - 2 + 3 - 4 +. .. прибавляем к 1 - 1 + 1 - 1 + ....

Итак . ${\ displaystyle s = {\ frac {1} {4}}}$

Хотя 1 - 2 + 3 - 4 + ... не имеет суммы в обычном смысле, уравнение s = 1 - 2 + 3 - 4 + ... = 1 ⁄ 4 может считаться наиболее естественным ответом, если такая сумма подлежит определению. Обобщенное определение «суммы» ряд расходящегося называется методом суммирования или методом суммирования . Существует много различных методов, и желательно, чтобы они разделяли некоторые расходящиеся ряды # Свойства методов суммирования Свойства обычного суммирования . Вышеупомянутые манипуляции на самом деле доказывают следующее: для любого метода суммирования, который является линейным и стабильным и суммирует ряды 1-2 + 3-4 + ... , полученная сумма равна 1 ⁄ 4 . Кроме того, поскольку

{\ displaystyle {\ begin {array} {rcllll} 2s & = && (1-2 + 3-4 + \ cdots) & + & (1-2 + 3-4 + \ cdots) \\ & = & 1 + {} & (-2 + 3-4 + \ cdots) & {} + 1-2 & {} + (3-4 + 5 \ cdots) \\ & = & 0 + {} & (- 2 + 3) + (3-4) + (- 4 + 5) + \ cdots \\ 2s & = && 1-1 + 1-1 \ cdots \ end {array}}}

такой метод также должен суммировать ряд Гранди как 1 - 1 + 1 - 1 + ... = 1 ⁄ 2 .

Продукт Коши

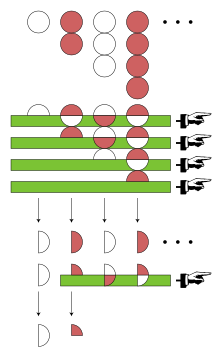
В 1891 году Эрнесто Чезаро выразил надежду, что расходящиеся ряды будут строго введены в исчисление , указав: «Уже пишут (1 - 1 + 1 - 1 + ...) ² = 1 - 2 + 3 - 4 + ... и утверждает, что обе стороны равны 1 ⁄ 4 ". Для Чезаро это уравнение было приложением теоремы, которую он опубликовал в прошлом году, которая является первой теоремой в истории суммируемых расходящихся рядов. Подробности о его методе суммирования приведены ниже ; Основная идея заключается в том , что 1 - 2 + 3 - 4 + ... является продукт Коши (дискретная свертка ) от 1 - 1 + 1 - 1 + ... с 1 - 1 + 1 - 1 + ... .

Произведение Коши двух бесконечных серий определено, даже если они оба расходятся. В случае, когда a _n = b _n = (−1) ⁿ , члены произведения Коши даются конечными диагональными суммами

{\ displaystyle {\ begin {array} {rcl} c_ {n} & = & \ displaystyle \ sum _ {k = 0} ^ {n} a_ {k} b_ {nk} = \ sum _ {k = 0} ^ {n} (- 1) ^ {k} (- 1) ^ {nk} \\ [1em] & = & \ displaystyle \ sum _ {k = 0} ^ {n} (- 1) ^ {n} = (- 1) ^ {n} (n + 1). \ End {array}}}

Тогда серия продуктов

{\ displaystyle \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} (n + 1) = 1-2 + 3-4 + \ cdots.}

Таким образом, метод суммирования, который учитывает произведение Коши двух рядов - и присваивает ряду 1 - 1 + 1 - 1 + ... сумму 1/2 - также присваивает ряду 1 - 2 + 3 - 4 +. .. сумма 1/4. С результатом предыдущего раздела это означает эквивалентность суммирования 1-1 + 1-1 + ... и 1-2 + 3-4 + ... с помощью методов, которые являются линейными, стабильными и соблюдают правила Коши. продукт.

Теорема Чезаро - тонкий пример. Ряд 1 - 1 + 1 - 1 + ... является суммируемым по Чезаро в самом слабом смысле, называемым (C, 1) -суммируемым, в то время как 1 - 2 + 3 - 4 + ... требует более сильной формы теоремы Чезаро , будучи (C, 2) -суммируемым. Поскольку все формы теоремы Чезаро линейны и стабильны, значения сумм вычислены выше.

Конкретные методы

Чезаро и Гёльдер

Данные о сумме (H, 2) 1 ⁄ 4

Чтобы найти (C, 1) сумму Чезаро 1-2 + 3-4 + ..., если она существует, необходимо вычислить средние арифметические частичные суммы ряда. Частичные суммы:

1, −1, 2, −2, 3, −3, ...,

и средние арифметические эти частичные суммы:

1, 0, 2 ⁄ 3 , 0, 3 ⁄ 5 , 0, 4 ⁄ 7 , ....

Эта последовательность средних не сходится, поэтому 1 - 2 + 3 - 4 + ... не суммируется по Чезаро.

Есть два хорошо известных обобщения суммирования Чезаро: концептуально более простым из них является последовательность (H, n ) методов для натуральных чисел n . Сумма (H, 1) - это суммирование по Чезаро, и более высокие методы повторяют вычисление средних. Выше четные средние сходятся к 1 ⁄ 2 , в то время как нечетные средние все равны 0, поэтому средние значения сходятся к среднему от 0 и 1 ⁄ 2 , а именно к 1 ⁄ 4 . Итак, 1-2 + 3-4 + ... (H, 2) суммируется до 1 ⁄ 4 .

«H» означает Отто Гёльдера , который впервые в 1882 году доказал то, что математики теперь считают связью между суммированием Абеля и суммированием (H, n ); 1 - 2 + 3 - 4 + ... был его первым примером. Тот факт, что 1 ⁄ 4 является (H, 2) суммой 1 - 2 + 3 - 4 + ..., гарантирует, что это также сумма Абеля; это также будет доказано непосредственно ниже.

Другое обычно формулируемое обобщение суммирования Чезаро - это последовательность (C, n ) методов. Было доказано, что суммирование (C, n ) и суммирование (H, n ) всегда дают одни и те же результаты, но имеют разную историческую основу. В 1887 году Чезаро вплотную подошел к определению суммирования (C, n ), но привел лишь несколько примеров. В частности, он суммировал 1 - 2 + 3 - 4 + ... до 1 ⁄ 4 методом, который можно перефразировать как (C, n ), но в то время он не был оправдан как таковой. Он формально определил (C, n) методы в 1890 году, чтобы сформулировать свою теорему о том, что произведение Коши (C, n ) -суммируемого ряда и (C, m ) -суммируемого ряда равно (C, m + n + 1) -суммируемый.

Суммирование Абеля

Некоторые частичные числа 1-2 x + 3 x ² + ...; 1 / (1 + х ) ² ; и лимиты на 1

В отчете 1749 года Леонард Эйлер признает, что ряды расходятся, но все равно готовится подвести итоги:

... когда говорят, что сумма этого ряда 1 - 2 + 3 - 4 + 5 - 6 и т. д. равна 1 ⁄ 4 , это должно выглядеть парадоксально. Для добавления 100 членов этого ряда, получает -50, однако, сумма 101 терминов дает +51, который довольно сильно отличается от 1 / 4 и становится еще больше , когда один увеличивается число слагаемыхов. Но я уже раньше заметил, что необходимо придать слову сумма более широкое значение ...

Эйлер несколько раз предлагал обобщение слова «сумма». В случае 1-2 + 3-4 + ... его идеи похожи на то, что теперь известно как суммирование Абеля :

... больше не вызывает сомнений, что сумма этого ряда 1-2 + 3-4 + 5 и т. д. равна 1 ⁄ 4 ; поскольку он возникает в результате расширения формулы 1 ⁄ (1 + 1) ² , значение которой, бесспорно, равно 1 ⁄ 4 . Идея становится более ясной, если рассмотреть общий ряд 1 - 2 x + 3 x ² - 4 x ³ + 5 x ⁴ - 6 x ⁵ + и т. Д. которое возникает при расширении выражения 1 ⁄ (1+ x ) ² , которому этот ряд действительно равен после того, как мы установим x = 1 .

Есть много способов увидеть это, по крайней мере, для абсолютных значений | х | <1 , Эйлер прав в том, что

{\ displaystyle 1-2x + 3x ^ {2} -4x ^ {3} + \ cdots = {\ frac {1} {(1 + x) ^ {2}}}.}.

Можно взять разложение Тейлора правой части или применить формальный процесс деления в столбик для многочленов . Начиная с левой стороны, можно проследить общие эвристики выше и попробовать умножения на (1 + х ) дважды или возведения в квадрат в геометрическую прогрессию 1 - х + х ² - ... . Эйлер, кажется, также предлагает дифференцировать последний ряд по члену.

С современной точки зрения, производящая функция 1 - 2 x + 3 x ² - 4 x ³ + ... не определяет функцию при x = 1 , поэтому значение не может быть просто подставлено в полученное выражение. Поскольку функция определена для всех | х | <1 , можно взять предел, когда x приближается к 1, и это определение суммы Абеля:

{\ displaystyle \ lim _ {x \ rightarrow 1 ^ {-}} \ sum _ {n = 1} ^ {\ infty} n (-x) ^ {n-1} = \ lim _ {x \ rightarrow 1 ^ {-}} {\ frac {1} {(1 + x) ^ {2}}} = {\ frac {1} {4}}.}

Эйлер и Борель

Суммирование по Эйлеру до 1 ⁄ 2 - 1 ⁄ 4 . Положительные значения показаны белым, отрицательные - коричневым, а сдвиги и отмены - зеленым.

Эйлер применил к этой серии другую технику: преобразование Эйлера , одно из его собственных изобретений. Чтобы вычислить преобразование Эйлера, нужно начать с последовательности положительных членов, составляющих чередующийся ряд - в данном случае 1, 2, 3, 4, .... Первый элемент этой последовательности помечен как ₀ .

Далее нужна последовательность прямых разностей между 1, 2, 3, 4, ... ; это всего лишь 1, 1, 1, 1, .... Первый элемент этой последовательности помечен как Δ a ₀ . Эйлера преобразования также зависит от различий различий и высших итераций , но все вперед различие между 1, 1, 1, 1, ... являются преобразования 0. Эйлера 1 - 2 + 3 - 4 + ... есть затем определяется как

{\ displaystyle {\ frac {1} {2}} a_ {0} - {\ frac {1} {4}} \ Delta a_ {0} + {\ frac {1} {8}} \ Delta ^ {2 } a_ {0} - \ cdots = {\ frac {1} {2}} - {\ frac {1} {4}}.}

В современной терминологии, один говорят , что 1 - 2 + 3 - 4 + ... является Euler суммирует к 1 / 4 .

Суммируемость по Эйлеру также подразумевает суммируемость по Борелю с тем же значением суммирования, что и в общем случае.

Разделение весов

Сайчев и Войчинский приходят к 1 - 2 + 3 - 4 + ... = 1 ⁄ 4 , применяя только два физических принципа: бесконечно малую релаксацию и разделение шкал . Чтобы быть точным, эти принципы приводят их для определения широкого семейства « $ф$ методов -суммирования», все из которых подводят серию до 1 / 4 :

Если $φ$ ( x ) - функция, первая и вторая производные которой непрерывны и интегрируемы на (0, ∞), такая, что φ (0) = 1 и пределы φ ( x ) и x φ ( x ) в + ∞ равны оба 0, то ${\ displaystyle \ lim _ {\ delta \ rightarrow 0} \ sum _ {m = 0} ^ {\ infty} (- 1) ^ {m} (m + 1) \ varphi (\ delta m) = {\ frac {1} {4}}.}$

Этот результат обобщает суммирование Абеля, которое восстанавливается положением $φ$ ( x ) = exp (- x ). Общее утверждение можно доказать, разделив члены ряда по m и преобразовав выражение в интеграл Римана . Для последнего шага соответствующее доказательство для 1 - 1 + 1 - 1 + ... применяет теорему о среднем значении , но здесь нужна более сильная форма Лагранжа теоремы Тейлора .

Обобщение

Выдержка из п. 233 E212 - Institutiones Calculi Differenceis cum eius usu in analysi finitorum ac doctrina serierum . Эйлер суммирует аналогичный ряд, ок. 1755.

Трехкратное произведение Коши чисел 1 - 1 + 1 - 1 + ... равно 1 - 3 + 6 - 10 + ..., чередующемуся ряду треугольных чисел ; его Абель и Эйлера сумма равна 1 / 8 . Четырехкратное произведение Коши 1 - 1 + 1 - 1 + ... равно 1 - 4 + 10 - 20 + ..., чередующемуся ряду тетраэдрических чисел , сумма Абеля которых равна 1 ⁄ 16 .

Другое обобщение 1 - 2 + 3 - 4 + ... в несколько ином направлении - это ряд 1 - 2 ⁿ + 3 ⁿ - 4 ⁿ + ... для других значений n . Для натуральных чисел n эти серии имеют следующие суммы Абеля:

{\ displaystyle 1-2 ^ {n} + 3 ^ {n} - \ cdots = {\ frac {2 ^ {n + 1} -1} {n + 1}} B_ {n}}

где B _n - числа Бернулли . Для четного n это сводится к

{\ displaystyle 1-2 ^ {2k} + 3 ^ {2k} - \ cdots = 0,}

что можно интерпретировать как утверждение, что отрицательные четные значения дзета-функции Римана равны нулю. Эта сумма стала предметом особой насмешки со стороны Нильса Хенрика Абеля в 1826 году:

Дивергентные серии - это, по сути, дело дьявола, и жаль, что кто-то осмеливается найти какие-либо доказательства на их основе. Из них можно получить все, что угодно, если использовать их, и именно они сделали так много несчастий и так много парадоксов. Можно ли придумать что-нибудь более ужасное, чем сказать, что

0 = 1-2 ²ⁿ + 3 ²ⁿ - 4 ²ⁿ + и т. Д.

где n - положительное число. Здесь есть над чем посмеяться, друзья.

Учитель Чезаро, Эжен Шарль Каталан , также пренебрежительно относился к расходящимся сериям. Под влиянием Каталонии Чезаро первоначально называл «обычные формулы» для 1-2 ⁿ + 3 ⁿ - 4 ⁿ + ... «абсурдными равенствами», а в 1883 году Чезаро выразил типичное для того времени мнение, что формулы были ложными. но все же как-то формально полезно. Наконец, в своей работе 1890 г. « Sur la multiplication des séries» Чезаро использовал современный подход, начиная с определений.

Ряды также изучаются для нецелых значений n ; они составляют эту функцию Дирихле . Частью мотивации Эйлера к изучению рядов, связанных с 1 - 2 + 3 - 4 + ..., было функциональное уравнение эта-функции, которое непосредственно ведет к функциональному уравнению дзета-функции Римана . Эйлер уже прославился тем, что нашел значения этих функций в положительных четных целых числах (включая проблему Базеля ), и он также пытался найти значения в положительных нечетных целых числах (включая константу Апери ), проблема, которая до сих пор остается неуловимой. . В частности, с этой функцией легче работать методами Эйлера, потому что ее ряд Дирихле суммируем по Абелю всюду; ряды Дирихле дзета-функции гораздо труднее просуммировать там, где они расходятся. Например, аналог 1 - 2 + 3 - 4 + ... в дзета-функции - это не чередующийся ряд 1 + 2 + 3 + 4 + ... , который имеет глубокое применение в современной физике, но требует гораздо более сильного методы суммирования.

Смотрите также

Сноски

Алабдулмохсин, Ибрагим М. (2018). «Аналитическая теория суммируемости». Исчисление суммируемости . Издательство Springer International. С. 65–91. DOI : 10.1007 / 978-3-319-74648-7_4 .
Билс, Ричард (2004). Анализ: Введение . Кембридж UP. ISBN 978-0-521-60047-7.
Дэвис, Гарри Ф. (май 1989 г.). Ряды Фурье и ортогональные функции . Дувр. ISBN 978-0-486-65973-2.
Эйлер, Леонард; Уиллис, Лукас; Ослер, Томас Дж. (2006). «Перевод с примечаниями к статье Эйлера: Замечания о прекрасном соотношении между прямым и обратным степенным рядами» . Эйлеров архив . Проверено 22 марта 2007 .Первоначально опубликовано как Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Mémoires de l'Académie des Sciences de Berlin . 17 : 83–106.
Ферраро, Джованни (июнь 1999 г.). "Первое современное определение суммы расходящегося ряда: аспект подъема математики 20-го века". Архив истории точных наук . 54 (2): 101–135. DOI : 10.1007 / s004070050036 .
Граттан-Гиннесс, Айвор (1970). Развитие основ математического анализа от Эйлера до Римана . MIT Press. ISBN 978-0-262-07034-8.
Харди, Г. Х. (1949). Расходящиеся серии . Кларендон Пресс. xvi + 396. ISBN 978-0-8218-2649-2. LCCN 49005496 . Руководство по ремонту 0030620 . OCLC 808787 .2-е изд. опубликовано Chelsea Pub. Co., 1991. LCCN 91-75377 . ISBN 0-8284-0334-1 .
Клайн, Моррис (ноябрь 1983 г.). «Эйлер и бесконечный ряд». Математический журнал . 56 (5): 307–314. CiteSeerX 10.1.1.639.6923 . DOI : 10.2307 / 2690371 . JSTOR 2690371 .
Кнопп, Конрад (1990). Теория и применение бесконечных рядов . Нью-Йорк: Dover Publications. ISBN 0486661652. LCCN 89071388 .
Лавин, Шауган (1994). Понимание бесконечного . Гарвард UP. ISBN 978-0-674-92096-5.
Маркусевич, Алексей Иванович (1967). Серия: фундаментальные концепции с историческим изложением (английский перевод 3-го переработанного издания (1961 г.) на русском языке). Дели, Индия: паб Hindustan. Corp. p. 176. LCCN sa68017528 . OCLC 729238507 .Автор также известен как А.И. Маркушевич и Алексей Иванович Маркочевич. Также опубликовано в Бостоне, Mass by Heath, OCLC 474456247 . Дополнительно OCLC 208730 , OCLC 487226828 .
Сайчев А.И.; Войчинский, WA (1996). Распределения по физическим и техническим наукам, Том 1 . Birkhaüser. ISBN 978-0-8176-3924-2.
Шауер, Брюс; Уотсон, Брюс (1994). Борелевские методы суммирования: теория и применение . Оксфордские математические монографии. Clarendon Press, Oxford University Press, Нью-Йорк. ISBN 0-19-853585-6. Руководство по ремонту 1320266 .
Туччароне, Джон (январь 1973 г.). «Развитие теории суммируемых расходящихся рядов с 1880 по 1925 год». Архив истории точных наук . 10 (1–2): 1–40. DOI : 10.1007 / BF00343405 .
Вретблад, Андерс (2003). Фурье-анализ и его приложения . Springer. ISBN 978-0-387-00836-3.

Languages

In other projects