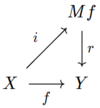Кофибрация - Cofibration

В математике , в частности в теории гомотопий , непрерывное отображение

{\ displaystyle i: от A \ до X}

,

где и являются топологическими пространствами , является корасслоением, если оно позволяет расширять гомотопические классы отображений до гомотопических классов отображений всякий раз, когда отображение может быть расширено до отображения, где , следовательно, связанные с ними гомотопические классы равны . ${\ displaystyle A}$ ${\ displaystyle X}$ ${\ displaystyle [A, S]}$ ${\ displaystyle [X, S]}$ ${\ displaystyle f \ in {\ text {Hom}} _ {\ textbf {Top}} (A, S)}$ ${\ displaystyle f '\ in {\ text {Hom}} _ {\ textbf {Top}} (X, S)}$ ${\ displaystyle f '\ circ i = f}$ ${\ Displaystyle [е] = [е '\ circ i]}$

Этот тип структуры может быть закодирован при техническом условии наличия свойства гомотопического расширения по отношению ко всем пространствам . Это определение двойственно определению расслоения , которое требуется для выполнения свойства гомотопического подъема по отношению ко всем пространствам. Эта двойственность неофициально называется двойственностью Экмана – Хилтона . В силу общности это техническое состояние заявлено, его можно использовать в категориях моделей . ${\ displaystyle S}$

Определение

Теория гомотопии

В дальнейшем через обозначим единичный интервал. ${\ Displaystyle I = [0,1]}$

Карта топологических пространств называется корасслоением ^{pg 51,} если для любой карты , для которой существует расширение , то есть существует такая карта , что мы можем продолжить гомотопию отображений до гомотопии отображений , где ${\ Displaystyle я \ двоеточие от А \ до Х}$ ${\ displaystyle f: от A \ до S}$ ${\ displaystyle X}$ ${\ displaystyle f ': от X \ до S}$ ${\ displaystyle f '\ circ i = f}$ ${\ displaystyle H: A \ times I \ to S}$ ${\ displaystyle H ': X \ times I \ to S}$

${\ displaystyle {\ begin {align} H (a, 0) & = f (a) \\ H '(x, 0) & = f' (x) \ end {align}}}$

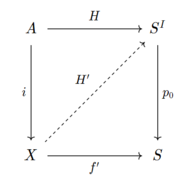
Мы можем закодировать это условие в следующей коммутативной диаграмме

где есть пространство путей из . ${\ displaystyle S ^ {I} = {\ text {Hom}} _ {\ textbf {Top}} (I, S)}$ ${\ displaystyle S}$

Кофибрантные объекты

Для категории модели , например, для точечных топологических пространств, объект называется кофибрантным, если карта является кофибрантной. Обратите внимание, что в категории точечных топологических пространств понятие корасслоения совпадает с предыдущим определением, предполагающим, что карты являются точечными отображениями топологических пространств. ${\ Displaystyle {\ mathcal {M}}}$ ${\ displaystyle X}$ ${\ displaystyle * \ к X}$

Примеры

В топологии

Кофибрации - неудобный класс карт с вычислительной точки зрения, потому что их легче рассматривать как формальный технический инструмент, который позволяет «делать» теоретико-гомотопические построения с топологическими пространствами. Благо для любой карты

{\ displaystyle f: от X \ до Y}

топологических пространств существует ассоциированное корасслоение с пространством, называемым цилиндром отображения (где - деформационный ретракт, следовательно, гомотопически эквивалентный ему), которое имеет индуцированное корасслоение, называемое заменой отображения на копослоение. ${\ displaystyle Mf}$ ${\ displaystyle Y}$

{\ displaystyle i: X \ to Mf}

и карта, через которую проходят факторы, что означает, что существует коммутативная диаграмма ${\ displaystyle Mf \ to Y}$ ${\ displaystyle f}$

где - гомотопическая эквивалентность. ${\ displaystyle r}$

В дополнение к этому классу примеров есть

Часто используемое в том, что сотовое включение корасслоение (так, например, если это пара CW , то есть корасслоение). Это следует из предыдущего факта, так как это кофибрация для каждого , а выталкивания - это карты приклеивания к скелету. ${\ Displaystyle (Х, А)}$ ${\ Displaystyle от А \ до Х}$ ${\ Displaystyle S ^ {n-1} \ к D ^ {n}}$ ${\ displaystyle n}$ ${\ displaystyle n-1}$
Софибрации сохраняются под вытяжками и составом, о котором подробно говорится ниже.

В цепных комплексах

Если мы позволим быть категорией цепных комплексов, которые находятся в степенях , то существует структура модельной категории ^{pg 1.2, в} которой слабые эквивалентности являются квазиизоморфизмами , поэтому отображения цепных комплексов, которые являются изоморфизмами после взятия когомологий, расслоения являются просто эпиморфизмами и кофибрации задаются картами ${\ Displaystyle С _ {+} ({\ mathcal {A}})}$ ${\ displaystyle 0}$ ${\ displaystyle q << 0}$

${\ displaystyle i: C _ {\ bullet} \ to D _ {\ bullet}}$

которые инъективны, а коядровый комплекс представляет собой комплекс проективных объектов в . Кроме того, софибрантные объекты - это комплексы, все объекты которых являются проективными объектами . ${\ displaystyle {\ text {Coker}} (я) _ {\ bullet}}$ ${\ displaystyle {\ mathcal {A}}}$ ${\ displaystyle {\ mathcal {A}}}$

Полусимплициальные множества

Для категории полусимплициальных множеств ^{pg 1.3} (что означает отсутствие отображений ко-вырожденности, повышающихся по степени), существует структура модельной категории с расслоениями, заданными Kan-расслоениями, инъективными отображениями кофибраций и слабыми эквивалентностями, задаваемыми слабыми эквивалентностями после геометрической реализации. ${\ displaystyle ss {\ textbf {Set}}}$

Характеристики

Для хаусдорфовых пространств каждое корасслоение является замкнутым включением (инъективным с замкнутым образом); результат также обобщается на слабые хаусдорфовы пространства .
Кодекартов Квадрат из корасслоения является корасслоением. То есть, если есть любое (непрерывное) отображение (между компактно порожденными пространствами) и является корасслоением, то индуцированное отображение является корасслоением. ${\ displaystyle g \ двоеточие от A \ до B}$ ${\ Displaystyle я \ двоеточие от А \ до Х}$ ${\ displaystyle B \ to B \ cup _ {g} X}$
Цилиндр отображения может быть понято как Кодекартов Квадрат из и вложения (на одном конце единичного интервала) . То есть цилиндр отображения можно определить как . К универсальному свойству в Кодекартовом Квадрате, является корасслоением именно тогда , когда отображение цилиндра можно построить для любого пространства X . ${\ Displaystyle я \ двоеточие от А \ до Х}$ ${\ displaystyle i_ {0} \ двоеточие от A \ до A \ times I}$ ${\ Displaystyle Ми = Х \ чашка _ {я} (А \ раз I)}$ ${\ displaystyle i}$
Каждую карту можно заменить кофибровкой через конструкцию цилиндра отображения . То есть для произвольного (непрерывного) отображения (между компактно порожденными пространствами) определяется цилиндр отображения ${\ displaystyle f \ двоеточие от X \ до Y}$

{\ Displaystyle Mf = Y \ чашка _ {f} (X \ times I)}

.

Затем он распадается на композицию кофаслоения и гомотопической эквивалентности . То есть можно записать как карту

{\ displaystyle f}

{\ displaystyle f}

{\ displaystyle X {\ xrightarrow {j}} Mf {\ xrightarrow {r}} Y}

с , когда это включение, и на и на .

{\ displaystyle f = rj}

{\ displaystyle j \ двоеточие x \ mapsto (x, 0)}

{\ displaystyle r \ двоеточие y \ mapsto y}

{\ displaystyle Y}

{\ Displaystyle р \ двоеточие (х, s) \ mapsto f (x)}

{\ Displaystyle X \ раз I}

Существует кофибрация ( A , X ) тогда и только тогда, когда есть ретракция из в , поскольку это выталкивание и, таким образом, индуцирует отображение в каждое пространство, которое можно увидеть на диаграмме. ${\ Displaystyle X \ раз I}$ ${\ Displaystyle (А \ раз I) \ чашка (Х \ раз \ {0 \})}$
Аналогичные эквивалентности могут быть заявлены для пар деформация-ретракт и для соседних пар деформация-ретракт.

Конструкции с кофибрациями

Замена кофибранта

Обратите внимание, что в категории модели, если это не кофибрация, цилиндр отображения образует замену софибранта . Фактически, если мы работаем только с категорией топологических пространств, кофибрантная замена для любого отображения из точки в пространство образует кофибрантную замену. ${\ Displaystyle {\ mathcal {M}}}$ ${\ displaystyle i: * \ к X}$ ${\ displaystyle Mi}$

Cofiber

Для корасслоения мы определяем кофайбер как индуцированное фактор-пространство . В общем, для , то cofiber ^{пг 59} определяется как фактор - пространство ${\ Displaystyle от А \ до Х}$ ${\ Displaystyle X / A}$ ${\ displaystyle f: от X \ до Y}$

${\ displaystyle C_ {f} = M_ {f} / (A \ times \ {0 \})}$

который является конусом отображения . Гомотопически кофайбер действует как гомотопическое коядро карты . В самом деле, для остроконечных топологических пространств гомотопически копределом из ${\ displaystyle f}$ ${\ displaystyle f: от X \ до Y}$

${\ displaystyle {\ underset {\ to} {\ text {hocolim}}} \ left ({\ begin {matrix} X & \ xrightarrow {f} & Y \\\ downarrow && \\ * \ end {matrix}} \ right ) = C_ {f}}$

Фактически, последовательность карт снабжена последовательностью cofiber, которая действует как выделенный треугольник в триангулированных категориях. ${\ Displaystyle от X \ до Y \ до C_ {f}}$

Смотрите также

использованная литература

^ ^а ^б Мэй, Дж. Питер. (1999). Краткий курс алгебраической топологии . Чикаго: Издательство Чикагского университета. ISBN 0-226-51182-0. OCLC 41266205 .
^ ^a ^b Квиллен, Дэниел Г. (1967). Гомотопическая алгебра . Берлин: Springer-Verlag. ISBN 978-3-540-03914-3. OCLC 294862881 .

Питер Мэй, «Краткий курс алгебраической топологии» : глава 6 определяет и обсуждает кофибрации, и они используются повсюду.
Рональд Браун, «Топология и группоиды» ; Глава 7 озаглавлена «Софибрации» и дает много результатов, нигде больше не найденных.

[:0-1] а ^б Мэй, Дж. Питер. (1999). Краткий курс алгебраической топологии . Чикаго: Издательство Чикагского университета. ISBN 0-226-51182-0. OCLC 41266205 .

[:1-2] Квиллен, Дэниел Г. (1967). Гомотопическая алгебра . Берлин: Springer-Verlag. ISBN 978-3-540-03914-3. OCLC 294862881 .

Languages

In other projects