Треугольная черепица - Triangular tiling

Треугольная черепица

Тип	Обычная черепица
Конфигурация вершины	3.3.3.3.3.3 (или 3 ⁶ )
Конфигурация лица	V6.6.6 (или V6 ³ )
Символ (ы) Шлефли	{3,6} {3 ^[3] }
Символ (ы) Wythoff	6 \| 3 2 3 \| 3 3 \| 3 3 3
Диаграмма (ы) Кокстера	знак равно
Симметрия	p6m , [6,3], (* 632)
Симметрия вращения	p6 , [6,3] ⁺ , (632) p3 , [3 ^[3] ] ⁺ , (333)
Двойной	Шестиугольная черепица
Характеристики	Вершинно-транзитивный , реберно-транзитивный , гранно-транзитивный

В геометрии , то треугольные плиточный или треугольная тесселяция является одним из трех регулярных разбиений в евклидовой плоскости , и является единственным таким плиточной , где составными формы не являются parallelogons . Поскольку внутренний угол равностороннего треугольника составляет 60 градусов, шесть треугольников в точке занимают полные 360 градусов. Треугольная мозаика имеет символ Шлефли {3,6}.

Конвей называет это дельтильей , названной в честь треугольной формы греческой буквы дельта (Δ). Треугольная мозаика также может быть названа кишекстилем с помощью операции кис, которая добавляет центральную точку и треугольники для замены граней гексилля .

Это одна из трех правильных мозаик плоскости . Два других - это квадратная и шестиугольная мозаика .

Равномерная окраска

2-однородная треугольная мозаика, 4 цветных треугольника, связанных с геодезическим многогранником как {3,6+} _2,0 .

Существует 9 различных однородных расцветок треугольной мозаики. (Назовите цвета индексами на 6 треугольниках вокруг вершины: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Три из них могут быть получены из других, повторяя цвета: 111212 и 111112 из 121213 по объединение 1 и 3, а 111213 уменьшено с 121314.

Существует один класс раскраски Архимеда , 111112, (отмеченный знаком *), который не является 1-однородным и содержит чередующиеся ряды треугольников, в которых окрашена каждая третья. Показанный пример является 2-однородным, но существует бесконечно много таких архимедовых раскрасок, которые можно создать произвольным горизонтальным сдвигом строк.

111111	121212	111222	112122	111112 (*)

p6m (* 632)	p3m1 (* 333)	см (2 * 22)	p2 (2222)	p2 (2222)

121213	111212	111112	121314	111213

p31m (3 * 3)			п3 (333)

Решетчатые и круглые упаковки А2

А^*
₂ решетка в виде трех треугольных мозаик:

+

Расположение вершин треугольного тайлинга называется решеткой A ₂ . Это двумерный случай простых сот .

А^*
₂ решетка (также называемая A³
₂) может быть построена путем объединения всех трех решеток A ₂ и эквивалентна решетке A ₂ .

+

= двойной

знак равно

Вершины треугольной мозаики являются центрами максимально плотной упаковки кругов . Каждый круг находится в контакте с 6 другими кругами в упаковке ( число поцелуев ). Плотность упаковки $π$ ⁄ √ 12 или 90,69%. Вороного клетки треугольной плитки является шестиугольником , и поэтому Вороной тесселяция , гексагональной черепица, имеют прямое соответствие к окружности упаковке.

Геометрические вариации

Треугольные мозаики могут быть построены с такой же топологией {3,6}, что и обычные мозаики (6 треугольников вокруг каждой вершины). Для одинаковых граней ( транзитивность граней ) и транзитивность вершин существует 5 вариантов. Приведенная симметрия предполагает, что все грани одного цвета.

Симметрия скаленового треугольника
p2
Симметрия скаленового треугольника
pmg
Равнобедренный треугольник
cmm симметрия
Прямоугольный треугольник cmm симметрия
Равносторонний треугольник
симметрия p6m

Связанные многогранники и мозаики

Плоские мозаики связаны с многогранниками . Помещение меньшего количества треугольников на вершину оставляет зазор и позволяет сложить его в пирамиду . Их можно расширить до Платоновых тел : пять, четыре и три треугольника на вершине определяют икосаэдр , октаэдр и тетраэдр соответственно.

Это разбиение топологически связано как часть последовательности правильных многогранников с символами Шлефли {3, n}, продолжающихся в гиперболическую плоскость .

* n 32 изменение симметрии правильных мозаик: {3, n } v т е
Сферический				Евклид.	Компактный гипер.		Paraco.	Некомпактный гиперболический

3.3	3 ³	3 ⁴	3 ⁵	3 ⁶	3 ⁷	3 ⁸	3 ^∞	3 ¹²ⁱ	3 ⁹ⁱ	3 ⁶ⁱ	3 ³ⁱ

Он также топологически связан как часть последовательности каталонских тел с конфигурацией граней Vn.6.6, а также продолжается в гиперболической плоскости.

V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6

Конструкции Wythoff из шестиугольных и треугольных мозаик

Как и в случае однородных многогранников, существует восемь однородных мозаик, которые могут быть основаны на правильном шестиугольном мозаике (или двойном треугольном мозаике).

Рисуя плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, мы получаем 8 форм, 7 из которых топологически различны. ( Усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные / треугольные мозаики
Фундаментальные области	Симметрия : [6,3], (* 632)							[6,3] ⁺ , (632)
	{6,3}	т {6,3}	г {6,3}	т {3,6}	{3,6}	рр {6,3}	tr {6,3}	sr {6,3}


Конфиг.	6 ³	3.12.12	(6,3) ²	6.6.6	3 ⁶	3.4.6.4	4.6.12	3.3.3.3.6

Треугольные мозаики симметрии v т е
Wythoff	3 \| 3 3	3 3 \| 3	3 \| 3 3	3 3 \| 3	3 \| 3 3	3 3 \| 3	3 3 3 \|	\| 3 3 3
Coxeter
Изображение Вершина фигура	(3,3) ³	3.6.3.6	(3,3) ³	3.6.3.6	(3,3) ³	3.6.3.6	6.6.6	3.3.3.3.3.3

Связанные регулярные сложные апейрогоны

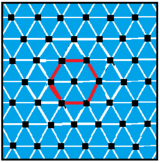
Есть 4 правильных комплексных апейрогона , разделяющих вершины треугольной мозаики. У правильных сложных апейрогонов есть вершины и ребра, причем ребра могут содержать 2 и более вершины. Регулярные апейрогоны p { q } r ограничены: 1 / p + 2 / q + 1 / r = 1. Ребра имеют p вершин, а фигуры вершин r -угольные.

Первый состоит из двух ребер, следующие два - треугольные, а последний имеет перекрывающиеся шестиугольные ребра.

2 {6} 6 или	3 {4} 6 или	3 {6} 3 или	6 {3} 6 или

Другие треугольные мозаики

Также существуют три плитки Лавеса, состоящие из однотипных треугольников:

Kisrhombille 30 ° -60 ° -90 ° прямоугольные треугольники	Кисквадриль 45 ° -45 ° -90 ° прямоугольные треугольники	Кисделтиль 30 ° -30 ° -120 ° равнобедренные треугольники

Смотрите также

Треугольная черепица сотовая
Простые соты
Замощения правильных многоугольников
Список однородных мозаик
Изогрид (конструктивное проектирование с использованием треугольной черепицы)

использованная литература

Coxeter, HSM Regular Polytopes , (3-е издание, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Таблица II: Обычные соты
Грюнбаум, Бранко и Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1.(Глава 2.1: Регулярные и однородные мозаики , стр. 58-65, Глава 2.9 Архимедовы и однородные раскраски, стр. 102–107)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X. p35
Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]

внешние ссылки

Вайсштейн, Эрик В. «Треугольная сетка» . MathWorld .
- Вайсштейн, Эрик В. «Обычная мозаика» . MathWorld .
- Вайсштейн, Эрик В. «Равномерная мозаика» . MathWorld .
Клитцинг, Ричард. «Двумерные евклидовы мозаики x3o6o - trat - O2» .

v т е Фундаментальные выпуклые регулярные и однородные соты размером 2-9
Космос	Семья	${\ displaystyle {\ tilde {A}} _ {n-1}}$	${\ displaystyle {\ tilde {C}} _ {n-1}}$	${\ displaystyle {\ tilde {B}} _ {n-1}}$	${\ displaystyle {\ tilde {D}} _ {n-1}}$	${\ displaystyle {\ tilde {G}} _ {2}}$ / / ${\ displaystyle {\ tilde {F}} _ {4}}$ ${\ displaystyle {\ tilde {E}} _ {n-1}}$
E ²	Равномерная черепица	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Шестиугольный
E ³	Равномерно выпуклые соты	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Равномерные 4-соты	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-ячеечные соты
E ⁵	Равномерные 5-соты	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Равномерные 6-соты	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Равномерные 7-соты	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Равномерное 8-соты	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Равномерные 9-соты	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Равномерные 10-соты	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Uniform ( n -1) - соты	{3 ^[n] }	δ _n	hδ _n	qδ _n	1 _к2 • 2 _к1 • к ₂₁

Languages

In other projects