Быстрый обратный квадратный корень - Fast inverse square root

Расчеты освещения и отражения (показанные здесь в шутере от первого лица OpenArena ) используют быстрый код обратного квадратного корня для вычисления углов падения и отражения.

Быстрая обратный квадратный корень , иногда называют Fast InvSqrt () или с помощью шестнадцатеричной константы 0x5F3759DF , представляет собой алгоритм , что оценки , тем обратный (или мультипликативные обратный) от квадратного корня из 32-битного с плавающей точкой числа в IEEE 754 с плавающими -точечный формат . Эта операция используется в цифровой обработке сигналов для нормализации вектора, т. Е. Масштабирования его до длины 1. Например, программы компьютерной графики используют обратные квадратные корни для вычисления углов падения и отражения для освещения и затенения . Алгоритм наиболее известен своей реализацией в 1999 году в исходном коде Quake III Arena , видеоигры -шутера от первого лица, в которой интенсивно использовалась трехмерная графика . Алгоритм только начал появляться на публичных форумах, таких как Usenet, в 2002 или 2003 годах. В то время вычисление обратного числа с плавающей запятой , как правило, было дорогостоящим с точки зрения вычислений, особенно в больших масштабах; быстрый обратный квадратный корень обошел этот шаг. ${\ displaystyle {\ frac {1} {\ sqrt {x}}}}$${\ displaystyle x}$

Алгоритм принимает на вход 32-битное число с плавающей запятой и сохраняет уменьшенное вдвое значение для дальнейшего использования. Затем, рассматривая биты, представляющие число с плавающей запятой как 32-битное целое число, выполняется логический сдвиг на один бит вправо, и результат вычитается из числа 0x 5F3759DF, которое является представлением с плавающей запятой приближенного значения . Это приводит к первому приближению обратного квадратного корня из входных данных. Снова обрабатывая биты как число с плавающей запятой, он выполняет одну итерацию метода Ньютона , что дает более точное приближение. ${\ displaystyle {\ sqrt {2 ^ {127}}}}$

Первоначально алгоритм был приписан Джону Кармаку , но расследование показало, что код имеет более глубокие корни как в аппаратной, так и в программной части компьютерной графики. Корректировки и изменения прошли как через Silicon Graphics, так и через 3dfx Interactive , причем реализация Гэри Таролли для SGI Indigo была самым ранним из известных способов использования. Исследование пролило некоторый свет на исходную константу, полученную в результате сотрудничества между Кливом Молером и Грегори Уолшем, в то время как Грегори работал в Ardent Computing в начале 1980-х годов.

С последующим усовершенствованием аппаратного обеспечения, особенно с инструкцией x86 SSErsqrtss , этот метод, как правило, неприменим к современным вычислениям, хотя он остается интересным примером как исторически, так и для более ограниченных машин, таких как недорогие встроенные системы. Однако все больше производителей встраиваемых систем включают тригонометрические и другие математические ускорители, такие как CORDIC , что устраняет необходимость в таких алгоритмах.

Мотивация

Нормали поверхности широко используются в расчетах освещения и затенения, что требует расчета норм для векторов. Здесь показано поле векторов, нормальных к поверхности.

Двумерный пример использования нормали для определения угла отражения от угла падения; в данном случае при отражении света от изогнутого зеркала. Быстрый обратный квадратный корень используется для обобщения этого вычисления на трехмерное пространство.${\ displaystyle C}$

Обратный квадратный корень из числа с плавающей запятой используется при вычислении нормализованного вектора . Программы могут использовать нормализованные векторы для определения углов падения и отражения . Программы трехмерной графики должны выполнять миллионы этих вычислений каждую секунду для имитации освещения. Когда код был разработан в начале 1990-х годов, большая часть вычислительной мощности с плавающей запятой отставала от скорости обработки целых чисел. Это было проблемой для программ 3D-графики до появления специализированного оборудования для обработки преобразований и освещения .

Длина вектора определяется вычислением его евклидовой нормы : квадратного корня из суммы квадратов компонентов вектора . Когда каждый компонент вектора делится на эту длину, новый вектор будет единичным вектором, указывающим в том же направлении. В графической программе 3D, все векторы в трехмерном мерном пространстве, так бы вектор . ${\ displaystyle {\ boldsymbol {v}}}$${\ displaystyle (v_ {1}, v_ {2}, v_ {3})}$

${\ displaystyle \ | {\ boldsymbol {v}} \ | = {\ sqrt {v_ {1} ^ {2} + v_ {2} ^ {2} + v_ {3} ^ {2}}}}$

- евклидова норма вектора.

${\ displaystyle {\ boldsymbol {\ hat {v}}} = {\ frac {\ boldsymbol {v}} {\ left \ | {\ boldsymbol {v}} \ right \ |}}}$

- нормализованный (единичный) вектор, используемый для представления . ${\ displaystyle \ | {\ boldsymbol {v}} \ | ^ {2}}$${\ displaystyle v_ {1} ^ {2} + v_ {2} ^ {2} + v_ {3} ^ {2}}$

${\ displaystyle {\ boldsymbol {\ hat {v}}} = {\ frac {\ boldsymbol {v}} {\ sqrt {\ left \ | {\ boldsymbol {v}} \ right \ | ^ {2}}} }}$

который связывает единичный вектор с обратным квадратным корнем из компонентов расстояния. Обратный квадратный корень можно использовать для вычисления, потому что это уравнение эквивалентно ${\ displaystyle {\ boldsymbol {\ hat {v}}}}$

${\ displaystyle {\ boldsymbol {\ hat {v}}} = {\ boldsymbol {v}} \, {\ frac {1} {\ sqrt {\ left \ | {\ boldsymbol {v}} \ right \ | ^ {2}}}}}$

где дробный член - это обратный квадратный корень из . ${\ displaystyle \ | {\ boldsymbol {v}} \ | ^ {2}}$

В то время деление с плавающей запятой было обычно дорого по сравнению с умножением; Быстрый алгоритм вычисления обратного квадратного корня обходит этап деления, что дает ему преимущество в производительности. Quake III Arena , шутер от первого лица , использовала быстрый алгоритм обратного извлечения квадратного корня для ускорения графических вычислений, но с тех пор этот алгоритм был реализован в некоторых специализированных аппаратных вершинных шейдерах с использованием программируемых вентильных матриц (FPGA).

Обзор кода

Следующий код представляет собой быструю реализацию метода обратного квадратного корня из Quake III Arena , лишенную директив препроцессора C , но содержащую точный исходный текст комментария:

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;                       // evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck? 
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

	return y;
}

В то время общий метод вычисления обратного квадратного корня заключался в том, чтобы вычислить приближение для , а затем пересмотреть это приближение с помощью другого метода, пока оно не попадет в допустимый диапазон ошибок фактического результата. Общие методы программного обеспечения в начале 1990-х годов основывались на приближении таблицы поиска . Ключом к быстрому обратному квадратному корню было прямое вычисление приближения с использованием структуры чисел с плавающей запятой, что оказалось быстрее, чем поиск в таблице. Алгоритм был примерно в четыре раза быстрее, чем вычисление квадратного корня другим методом и вычисление обратной величины с помощью деления с плавающей запятой. Алгоритм был разработан с учетом 32-битной спецификации с плавающей запятой IEEE 754-1985 , но исследование Криса Ломонта показало, что он может быть реализован в других спецификациях с плавающей запятой. ${\ displaystyle {\ frac {1} {\ sqrt {x}}}}$

Преимущества в скорости, обеспечиваемые трюком с обратным извлечением квадратного корня, связаны с обработкой 32-битного слова с плавающей запятой как целым числом и последующим вычитанием его из « магической » константы 0x 5F3759DF . Это целочисленное вычитание и битовый сдвиг приводит к битовому шаблону, который, если его переопределить как число с плавающей запятой, является грубым приближением для обратного квадратного корня из числа. Выполняется одна итерация метода Ньютона для получения некоторой точности, и код завершается. Алгоритм генерирует достаточно точные результаты с использованием уникального первого приближения для метода Ньютона ; однако он намного медленнее и менее точен, чем использование инструкции SSErsqrtss на процессорах x86, также выпущенных в 1999 году.

Согласно стандарту C, переинтерпретация значения с плавающей запятой как целого числа путем удаления указателя на него считается способным вызвать неожиданное поведение ( неопределенное поведение ). Эту проблему можно было обойти с помощью библиотечной функции memcpy. Следующий код соответствует стандартам C, хотя и за счет необходимости дополнительной переменной и увеличения памяти: значение с плавающей запятой помещается в анонимное объединение, содержащее дополнительный 32-разрядный целочисленный член без знака, и доступ к этому целому числу предоставляет бит вид уровня содержимого значения с плавающей запятой.

#include <stdint.h> // uint32_t
float Q_rsqrt( float number )
{	
	const float x2 = number * 0.5F;
	const float threehalfs = 1.5F;

	union {
		float f;
		uint32_t i;
	} conv  = { .f = number };
	conv.i  = 0x5f3759df - ( conv.i >> 1 );
	conv.f  *= threehalfs - ( x2 * conv.f * conv.f );
	return conv.f;
}

Однако прокалывание типов через объединение - это неопределенное поведение в C ++. Правильный способ сделать это в C ++ - готов std::bit_cast. Это также позволяет функции работать в constexprконтексте.

//only works after C++20 standard
#include <bit>
#include <limits>
#include <cstdint>

constexpr float Q_rsqrt(float number) noexcept
{
	static_assert(std::numeric_limits<float>::is_iec559); // (enable only on IEEE 754)

	float const y = std::bit_cast<float>(
        0x5f3759df - (std::bit_cast<std::uint32_t>(number) >> 1));
	return y * (1.5f - (number * 0.5f * y * y));
}

Пример работы

Например, число можно использовать для расчета . Первые шаги алгоритма проиллюстрированы ниже: ${\ displaystyle x = 0,15625}$${\ displaystyle {\ frac {1} {\ sqrt {x}}} \ приблизительно 2,52982}$

0011_1110_0010_0000_0000_0000_0000_0000  Bit pattern of both x and i
0001_1111_0001_0000_0000_0000_0000_0000  Shift right one position: (i >> 1)
0101_1111_0011_0111_0101_1001_1101_1111  The magic number 0x5F3759DF
0100_0000_0010_0111_0101_1001_1101_1111  The result of 0x5F3759DF - (i >> 1)

Интерпретация как 32-битное представление IEEE:

0_01111100_01000000000000000000000  1.25 × 2−3
0_00111110_00100000000000000000000  1.125 × 2−65
0_10111110_01101110101100111011111  1.432430... × 263
0_10000000_01001110101100111011111  1.307430... × 21

Повторная интерпретация этого последнего битового шаблона как числа с плавающей запятой дает приближение , которое имеет ошибку около 3,4%. После одной итерации метода Ньютона окончательный результат - ошибка всего 0,17%. ${\ displaystyle y = 2,61486}$${\ displaystyle y = 2,52549}$

Алгоритм

Алгоритм вычисляет , выполняя следующие шаги: ${\ displaystyle {\ frac {1} {\ sqrt {x}}}}$

1. Псевдоним аргумента к целому числу как способ вычисления приближения двоичного логарифма${\ displaystyle x}$ ${\ Displaystyle \ журнал _ {2} (х)}$
2. Используйте это приближение, чтобы вычислить приближение ${\ displaystyle \ log _ {2} \ left ({\ frac {1} {\ sqrt {x}}} \ right) = - {\ frac {1} {2}} \ log _ {2} (x) }$
3. Псевдоним обратно в число с плавающей запятой, как способ вычисления приближения экспоненты с основанием 2
4. Уточните приближение, используя одну итерацию метода Ньютона.

Представление с плавающей точкой

Поскольку этот алгоритм в значительной степени полагается на битовое представление чисел с плавающей запятой одинарной точности, здесь представлен краткий обзор этого представления. Чтобы закодировать ненулевое действительное число как число с плавающей запятой одинарной точности, первым делом нужно записать как нормализованное двоичное число: ${\ displaystyle x}$${\ displaystyle '' x ''}$

${\ displaystyle {\ begin {align} x & = \ pm 1.b_ {1} b_ {2} b_ {3} \ ldots \ times 2 ^ {e_ {x}} \\ & = \ pm 2 ^ {e_ { x}} (1 + m_ {x}) \ end {выровнено}}}$

где показатель степени является целым числом, и является двоичным представлением "мантиссы" . Поскольку единственный бит перед точкой в ​​мантиссе всегда равен 1, его не нужно сохранять. Из этой формы вычисляются три целых числа без знака: ${\ displaystyle e_ {x}}$${\ displaystyle m_ {x} \ in [0,1)}$${\ displaystyle 1.b_ {1} b_ {2} b_ {3} \ ldots}$${\ displaystyle (1 + m_ {x})}$

• ${\ displaystyle S_ {x}}$, То «знаковый бит», как если положительна и отрицательна или равна нулю (1 бит)${\ displaystyle 0}$${\ displaystyle x}$${\ displaystyle 1}$
• ${\ displaystyle E_ {x} = e_ {x} + B}$это «смещенная экспонента», где - « смещение экспоненты » (8 бит)${\ displaystyle B = 127}$
• ${\ Displaystyle M_ {x} = m_ {x} \ times L}$, где (23 бита)${\ displaystyle L = 2 ^ {23}}$

Затем эти поля упаковываются слева направо в 32-битный контейнер.

В качестве примера снова рассмотрим число . Нормализация урожайности: ${\ displaystyle x = 0,15625 = 0,00101_ {2}}$${\ displaystyle x}$

${\ Displaystyle х = + 2 ^ {- 3} (1 + 0,25)}$

и, таким образом, три беззнаковых целочисленных поля:

• ${\ displaystyle S = 0}$
• ${\ displaystyle E = -3 + 127 = 124 = 0111 \ 1100_ {2}}$
• ${\ displaystyle M = 0,25 \ times 2 ^ {23} = 2 \ 097 \ 152 = 0010 \ 0000 \ 0000 \ 0000 \ 0000 \ 0000_ {2}}$

эти поля упакованы, как показано на рисунке ниже:

Преобразование в целое число как приблизительный логарифм

Если бы вычисление производилось без компьютера или калькулятора, была бы полезна таблица логарифмов вместе с идентификатором , который действителен для каждой основы . Быстрый обратный квадратный корень основан на этом тождестве и на том факте, что преобразование float32 в целое число дает грубое приближение его логарифма. Вот как: ${\ displaystyle {\ frac {1} {\ sqrt {x}}}}$${\ displaystyle \ log _ {b} ({\ frac {1} {\ sqrt {x}}}) = \ log _ {b} (x ^ {- {\ frac {1} {2}}}) = - {\ frac {1} {2}} \ log _ {b} (x)}$${\ displaystyle b}$

Если положительное нормальное число : ${\ displaystyle x}$

${\ displaystyle x = 2 ^ {e_ {x}} (1 + m_ {x})}$

тогда

${\ displaystyle \ log _ {2} (x) = e_ {x} + \ log _ {2} (1 + m_ {x})}$

и поскольку логарифм в правой части может быть аппроксимирован выражением ${\ displaystyle m_ {x} \ in [0,1)}$

${\ displaystyle \ log _ {2} (1 + m_ {x}) \ приблизительно m_ {x} + \ sigma}$

где - свободный параметр, используемый для настройки приближения. Например, дает точные результаты на обоих концах интервала, а дает оптимальное приближение (лучшее в смысле равномерной нормы ошибки). ${\ displaystyle \ sigma}$${\ displaystyle \ sigma = 0}$${\ displaystyle \ sigma = {\ frac {1} {2}} - {\ frac {1+ \ ln (\ ln (2))} {2 \ ln (2)}} \ приблизительно 0,0430357}$

Целое число с псевдонимом числа с плавающей запятой (синим цветом) по сравнению с масштабированным и сдвинутым логарифмом (серым цветом).

Таким образом, существует приближение

${\ displaystyle \ log _ {2} (x) \ приблизительно e_ {x} + m_ {x} + \ sigma.}$

Интерпретация битового шаблона с плавающей запятой как целого числа дает ${\ displaystyle x}$${\ displaystyle I_ {x}}$

${\ displaystyle {\ begin {align} I_ {x} & = E_ {x} L + M_ {x} \\ & = L (e_ {x} + B + m_ {x}) \\ & = L (e_ {x} + m_ {x} + \ sigma + B- \ sigma) \\ & \ приблизительно L \ log _ {2} (x) + L (B- \ sigma). \ end {align}}}$

Тогда оказывается, что это масштабированная и сдвинутая кусочно-линейная аппроксимация , как показано на рисунке справа. Другими словами, аппроксимируется ${\ displaystyle I_ {x}}$${\ Displaystyle \ журнал _ {2} (х)}$${\ Displaystyle \ журнал _ {2} (х)}$

${\ displaystyle \ log _ {2} (x) \ приблизительно {\ frac {I_ {x}} {L}} - (B- \ sigma).}$

Первое приближение результата

Расчет основан на тождестве ${\ displaystyle y = {\ frac {1} {\ sqrt {x}}}}$

${\ displaystyle \ log _ {2} (y) = - {\ tfrac {1} {2}} \ log _ {2} (x)}$

Используя приближение логарифма выше, примененное к обоим и , приведенное выше уравнение дает: ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ frac {I_ {y}} {L}} - (B- \ sigma) \ приблизительно - {\ frac {1} {2}} \ left ({\ frac {I_ {x}} {L }} - (B- \ sigma) \ right)}$

Таким образом, приближение : ${\ displaystyle I_ {y}}$

${\ displaystyle I_ {y} \ приблизительно {\ tfrac {3} {2}} L (B- \ sigma) - {\ tfrac {1} {2}} I_ {x}}$

который записывается в коде как

i  = 0x5f3759df - ( i >> 1 );

Первый член выше - это магическое число

${\ displaystyle {\ tfrac {3} {2}} L (B- \ sigma) = {\ mathtt {0x5F3759DF}}}$

из чего можно сделать вывод . Второй член вычисляется путем сдвига битов на одну позицию вправо. ${\ displaystyle \ sigma \ приблизительно 0,0450466}$${\ displaystyle {\ frac {1} {2}} I_ {x}}$${\ displaystyle I_ {x}}$

Метод Ньютона

Относительная ошибка между прямым вычислением и быстрым обратным вычислением квадратного корня при выполнении 0, 1, 2, 3 и 4 итераций метода нахождения корня Ньютона. Обратите внимание, что принята двойная точность, и наименьшая представимая разница между двумя числами двойной точности достигается после выполнения 4 итераций.

В качестве обратного квадратного корня . Приближение, полученное на предыдущих этапах, можно уточнить с помощью метода поиска корня, метода , который находит нуль функции . Алгоритм использует метод Ньютона : если есть приближение для , то лучшее приближение можно вычислить, взяв , где - производная от at . Для выше , ${\ displaystyle y}$${\ displaystyle f (y) = {\ frac {1} {y ^ {2}}} - x = 0}$${\ displaystyle y_ {n}}$${\ displaystyle y}$${\ displaystyle y_ {n + 1}}$${\ displaystyle y_ {n} - {\ frac {f (y_ {n})} {f '(y_ {n})}}}$${\ displaystyle f '(y_ {n})}$${\ displaystyle f (y)}$${\ displaystyle y_ {n}}$${\ displaystyle f (y)}$

${\ displaystyle y_ {n + 1} = {\ frac {y_ {n} \ left (3-xy_ {n} ^ {2} \ right)} {2}}}$

где и . ${\ displaystyle f (y) = {\ frac {1} {y ^ {2}}} - x}$${\ displaystyle f '(y) = - {\ frac {2} {y ^ {3}}}}$

Рассмотрение числа с плавающей запятой эквивалентно ${\ displaystyle y}$y = y*(threehalfs - x/2*y*y);

${\ displaystyle y_ {n + 1} = y_ {n} \ left ({\ frac {3} {2}} - {\ frac {x} {2}} y_ {n} ^ {2} \ right) = {\ frac {y_ {n} \ left (3-xy_ {n} ^ {2} \ right)} {2}}.}$

Повторяя этот шаг, используя выходные данные функции ( ) в качестве входных данных следующей итерации, алгоритм приводит к сходимости к обратному квадратному корню. Для целей Quake III двигателя , была использована только одна итерация. Вторая итерация осталась в коде, но была закомментирована . ${\ displaystyle y_ {n + 1}}$${\ displaystyle y}$

Точность

График, показывающий разницу между эвристическим быстрым обратным квадратным корнем и прямым обращением квадратного корня, предоставляемым libstdc . (Обратите внимание на шкалу журнала по обеим осям.)

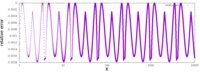
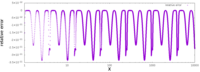
Как отмечалось выше, приближение удивительно точное. Единственный график справа отображает ошибку функции (то есть ошибку аппроксимации после того, как она была улучшена путем выполнения одной итерации метода Ньютона) для входных данных, начинающихся с 0,01, где стандартная библиотека дает в результате 10,0 , в то время как InvSqrt () дает 9,982522, что составляет разницу 0,0017478, или 0,175% от истинного значения, 10. С этого момента абсолютная ошибка только уменьшается, в то время как относительная ошибка остается в тех же пределах во всех порядках величины.

История

Исходный код Quake III не был выпущен до QuakeCon 2005 , но копии кода быстрого обратного квадратного корня появились в Usenet и других форумах уже в 2002 или 2003 годах. Первоначальные предположения указывали на Джона Кармака как на вероятного автора кода, но он возразил и предположил, что это написано Терье Матисеном, опытным программистом на ассемблере, который ранее помогал id Software с оптимизацией Quake . Матисен написал реализацию подобного фрагмента кода в конце 1990-х годов, но первоначальные авторы оказались намного дальше в истории компьютерной 3D-графики с реализацией Гэри Таролли для SGI Indigo в качестве возможного самого раннего известного использования. Рис Соммефельдт пришел к выводу, что оригинальный алгоритм был разработан Грегом Уолшем из Ardent Computer в консультации с Кливом Молером , создателем MATLAB . Клив Молер узнал об этом трюке из кода, написанного Уильямом Каханом и К.С. Нг в Беркли в 1986 году. Джим Блинн также продемонстрировал простое приближение обратного квадратного корня в столбце 1997 года для IEEE Computer Graphics and Applications . Пол Кинни реализовал быстрый метод для компьютера серии FPS T примерно в 1986 году. Система включала в себя векторную аппаратуру с плавающей запятой, которая не была богата целочисленными операциями. Значения с плавающей запятой были перемещены, чтобы можно было манипулировать для создания начального приближения.

Последующие улучшения

Магическое число

Точно неизвестно, как было определено точное значение магического числа. Крис Ломонт разработал функцию для минимизации ошибки аппроксимации путем выбора магического числа в диапазоне. Сначала он вычислил оптимальную константу для шага линейного приближения как 0x5F37642F , близкую к 0x5F3759DF , но эта новая константа дала немного меньшую точность после одной итерации метода Ньютона. Затем Ломонт искал оптимальную константу даже после одной и двух итераций по Ньютону и нашел 0x5F375A86 , который более точен, чем оригинал на каждой стадии итерации. В заключение он спросил, было ли выбрано точное значение исходной константы путем вывода или методом проб и ошибок . Ломонт сказал, что магическое число для 64-битного типа размера IEEE754 double - это 0x5FE6EC85E7DE30DA , но позже Мэтью Робертсон показал, что оно точно равно 0x5FE6EB50C7B537A9 . ${\ displaystyle R}$

Ян Кадлец уменьшил относительную ошибку еще в 2,7 раза за счет корректировки констант в одной итерации метода Ньютона, получив после исчерпывающего поиска в

	conv.i = 0x5F1FFFF9 - ( conv.i >> 1 );
	conv.f *= 0.703952253f * ( 2.38924456f - x * conv.f * conv.f );
	return conv.f;

Полный математический анализ для определения магического числа теперь доступен для чисел с плавающей запятой одинарной точности.

Нулевое нахождение

Промежуточным звеном к использованию одной и двух итераций метода Ньютона с точки зрения скорости и точности является одна итерация метода Галлея . В этом случае метод Галлея эквивалентен применению метода Ньютона с исходной формулой . Затем шаг обновления ${\ displaystyle f (y) = {\ frac {1} {y ^ {1/2}}} - xy ^ {3/2} = 0}$

${\ displaystyle y_ {n + 1} = y_ {n} - {\ frac {f (y_ {n})} {f '(y_ {n})}} = y_ {n} \ left ({\ frac { 3 + xy_ {n} ^ {2}} {1 + 3xy_ {n} ^ {2}}} \ right),}$

где реализация должна вычисляться только один раз через временную переменную. ${\ displaystyle xy_ {n} ^ {2}}$

Смотрите также

• Методы вычисления квадратных корней § Приближения, зависящие от представления с плавающей запятой
• Магическое число

Примечания

использованная литература

Библиография

дальнейшее чтение

• Кушнер, Дэвид (август 2002). «Волшебство Ид». IEEE Spectrum . 39 (8): 42–47. DOI : 10.1109 / MSPEC.2002.1021943 .

внешние ссылки

• 0x5f3759df , дальнейшие исследования точности и обобщения алгоритма Кристиана Плеснера Хансена
• Происхождение быстрого InvSqrt из Quake3 ()
• Исходный код Quake III Arena
• Реализация InvSqrt в DESMOS
• «Быстрый обратный квадратный корень - алгоритм Quake III» ( YouTube )