Занятый бобер - Busy beaver
В теоретической информатике игра о занятом бобре направлена на поиск завершающей программы заданного размера, которая дает максимально возможный результат. Поскольку легко придумать программу с бесконечным циклом, производящую бесконечный вывод, такие программы исключаются из игры.
Точнее, игра « занятого бобра» заключается в разработке останавливающейся машины Тьюринга с двоичным алфавитом, которая записывает на ленту наибольшее количество единиц, используя только заданный набор состояний. Правила игры с двумя состояниями следующие:
- машина должна иметь два состояния в дополнение к состоянию остановки, и
- лента изначально содержит только нули.
Игрок должен придумать таблицу переходов, нацеленную на максимальное количество единиц на ленте, при этом убедившись, что машина в конце концов остановится.
П - й занят бобер , BB- п или просто «занят бобр» машина Тьюринга , которая выигрывает п -ей государственную Busy Beaver игру. То есть он достигает наибольшего числа единиц среди всех других возможных машин Тьюринга, конкурирующих с n- состояниями. Машина Тьюринга BB-2 , например, достигает четырех 1s в шесть этапов.
Определение произвольной машина Тьюринга , является ли занят бобром неразрешимое . Это имеет значение для теории вычислимости , проблемы остановки и теории сложности . Эта концепция была впервые представлена Тибором Радо в его статье 1962 года «О невычислимых функциях».
Игра
Н -state занята игра бобер (или ВВ- н игра ), введенный в Тибор Рад 1962 бумаги «с, включает в себя класс машин Тьюринга , каждый член которой требуется , чтобы удовлетворять следующие требования к конструкции:
- Машина имеет n «рабочих» состояний плюс состояние остановки, где n - положительное целое число, и одно из n состояний определяется как начальное. (Обычно состояния обозначаются цифрами 1, 2, ..., n , с состоянием 1 в качестве начального состояния, или с помощью A , B , C , ..., с состоянием A в качестве начального состояния.)
- Машина использует одинарную двустороннюю бесконечную (или неограниченную) ленту.
- Алфавит ленты - {0, 1}, где 0 является пустым символом.
- Функция перехода машины принимает два входа:
- текущее состояние без остановки,
- символ в текущей ячейке ленты,
- и производит три выхода:
- символ для записи поверх символа в текущей ячейке ленты (это может быть тот же символ, что и перезаписанный символ),
- направление движения (влево или вправо; то есть сдвиг к ячейке ленты на одно место влево или вправо от текущей ячейки), и
- состояние, в которое нужно перейти (которое может быть состоянием остановки).
- Таким образом, существует (4 n + 4) 2 n n машин Тьюринга, удовлетворяющих этому определению, потому что общая форма формулы следующая ( символы × направления × ( состояния + 1)) ( символы × состояния ) .
- Функцию перехода можно рассматривать как конечную таблицу из 5 кортежей, каждая из которых имеет вид
- (текущее состояние, текущий символ, символ для записи, направление сдвига, следующее состояние).
«Запуск» машины состоит из запуска в начальном состоянии, при этом текущая ячейка ленты представляет собой любую ячейку пустой (все 0) ленты, а затем повторение функции перехода до тех пор, пока не будет введено состояние «Остановка» (если оно вообще возникнет). Если и только если машина в конце концов остановится, то количество единиц, окончательно оставшихся на ленте, называется счетом машины .
П -state заняты бобра (BB- п игра) является конкурсом , чтобы найти такой п -ей государственной машину Тьюринга , имеющую наибольшее количество очков - наибольшее количество 1s на своей ленту после приостановки. Машина , которая достигает максимально возможный балл среди всех п -state машин Тьюринга называется п -его государственным занят бобр, и машина , чья оценка является лишь высшим до сих пор достигли (возможно , не самой большого по возможности) называются чемпионом н -state машина.
Радо требовал, чтобы каждая машина, участвующая в конкурсе, сопровождалась заявлением о точном количестве шагов, необходимых для достижения состояния остановки, что позволяло проверить оценку каждой записи (в принципе), запустив машину для указанного числа. шагов. (Если бы записи состояли только из машинных описаний, тогда проблема проверки каждой потенциальной записи была бы неразрешимой, потому что она эквивалентна хорошо известной проблеме остановки - не было бы эффективного способа решить, останавливается ли в конечном итоге произвольная машина.)
Связанные функции
Функция занятого бобра Σ
Функция занятого бобра определяет максимальное количество баллов, которое может получить занятой бобер по заданному показателю. Это невычислимая функция . Кроме того, можно показать, что функция занятого бобра асимптотически растет быстрее, чем любая вычислимая функция.
Функция занятого бобра, Σ: ℕ → ℕ, определяется таким образом, что Σ ( n ) является максимально достижимой оценкой (максимальное количество единиц, в конечном итоге на ленте) среди всех останавливающихся двухсимвольных машин Тьюринга с n состояниями вышеупомянутых - описанного типа, когда запускался на пустой ленте.
Ясно, что Σ - хорошо определенная функция: для каждого n существует не более конечного числа n- состояний машин Тьюринга, как указано выше, с точностью до изоморфизма, следовательно, не более конечного числа возможных времен работы.
Эта бесконечная последовательность Σ является функцией занятого бобра , и любая двухсимвольная машина Тьюринга M с n состояниями, для которой σ ( M ) = Σ ( n ) (т. Е. Которая набирает максимальное количество очков), называется занятым бобрами . Обратите внимание, что для каждого n существует по крайней мере четыре занятых бобра с n состояниями (потому что, для любого занятого бобра с n состояниями, другой получается простым изменением направления сдвига при остановленном переходе, другой - смещением всех изменений направления на их противоположные. , и финал, изменив направление остановки занятого бобра, который полностью поменял местами).
Невычислимость
Работа Радо 1962 года доказала, что если f : ℕ → ℕ - любая вычислимая функция , то Σ ( n )> f (n) для всех достаточно больших n , и, следовательно, Σ не является вычислимой функцией.
Более того, это означает, что общий алгоритм не может решить , является ли произвольная машина Тьюринга занятой машиной. (Такой алгоритм не может существовать, потому что его существование позволило бы вычислить Σ, что является доказанной невозможностью. В частности, такой алгоритм мог бы использоваться для построения другого алгоритма, который вычислял бы Σ следующим образом: для любого данного n каждый из то конечное число п -state 2-символ Тьюринга машина будет испытана до тех пор , п -state занят бобр не найден, этот занят бобр машин будет затем моделируется , чтобы определить его счет, который по определению Е ( п )).
Несмотря на то, что Σ ( n ) - невычислимая функция, существуют некоторые маленькие n, для которых можно получить ее значения и доказать, что они верны. Нетрудно показать, что Σ (0) = 0, Σ (1) = 1, Σ (2) = 4, и со все большим трудом можно показать, что Σ (3) = 6 и Σ (4) = 13 (последовательность A028444 в OEIS ). Σ ( n ) еще не определено ни для одного случая n > 4, хотя нижние границы были установлены (см. Раздел « Известные значения » ниже).
В 2016 году Адам Едидиа и Скотт Ааронсон получили первую (явную) верхнюю оценку минимума n, для которого Σ ( n ) недоказуемо в ZFC . Для этого они построили машину Тьюринга с 7910 состояниями, поведение которой не может быть доказано на основе обычных аксиом теории множеств (теория множеств Цермело – Френкеля с аксиомой выбора ) при разумных гипотезах согласованности ( стационарное свойство Рамсея ). Позже это число было сокращено до 1919 состояний с устранением зависимости от стационарного свойства Рамсея, а затем до 748 состояний.
Сложность и недоказуемость Σ
Вариант колмогоровской сложности определяется следующим образом [ср. Boolos, Burgess & Jeffrey, 2007]: сложность числа n - это наименьшее количество состояний, необходимое для машины Тьюринга BB-класса, которая останавливается с помощью одного блока из n последовательных единиц на первоначально пустой ленте. Соответствующий вариант теоремы Чайтина о неполноте утверждает, что в контексте данной аксиоматической системы для натуральных чисел существует такое число k , что никакое конкретное число не может быть доказано, имеющее сложность больше k , и, следовательно, что нет конкретной верхней границы может быть доказано для Σ ( k ) (последнее из-за того, что «сложность n больше, чем k » было бы доказано, если бы было доказано « n > Σ ( k )»). Как упоминалось в цитируемой ссылке, для любой аксиоматической системы «обычной математики» наименьшее значение k, для которого это верно, намного меньше 10 ↑↑ 10 ; следовательно, в контексте обычной математики ни значение, ни верхняя граница Σ (10 ↑↑ 10) не могут быть доказаны. ( Первая теорема Гёделя о неполноте иллюстрируется этим результатом: в аксиоматической системе обычной математики есть истинное, но недоказуемое предложение вида «Σ (10 ↑↑ 10) = n », а истинных - бесконечно много. но недоказуемые предложения формы «Σ (10 ↑↑ 10) < n ».)
Функция максимального сдвига S
В дополнение к функции Е, Радо [+1962] ввел еще одну крайнюю функцию для BB-класса машин Тьюринга, то максимальные сдвиги функционировать , S , определяется следующим образом :
- s ( M ) = количество сдвигов, которые M делает перед остановкой, для любого M в E n ,
- S ( n ) = max { s ( M ) | M ∈ E n } = наибольшее количество сдвигов, сделанных любой останавливающейся двухсимвольной машиной Тьюринга с n состояниями.
Поскольку эти машины Тьюринга должны иметь сдвиг в каждом переходе или «шаге» (включая любой переход в состояние остановки), функция максимальных сдвигов одновременно является функцией максимальных шагов.
Радо показал, что S невычислима по той же причине, что и Σ - она растет быстрее, чем любая вычислимая функция. Он доказал это , просто отметив , что для каждого п , S ( п ) ≥ Σ ( п ). Каждый сдвиг может записывать на ленту 0 или 1, в то время как Σ считает подмножество сдвигов, которые записали 1, а именно те, которые не были перезаписаны к моменту остановки машины Тьюринга; следовательно, S растет по крайней мере так же быстро, как Σ, которая, как уже было доказано, растет быстрее, чем любая вычислимая функция.
Следующая связь между Σ и S была использована Лином и Радо [ Компьютерные исследования проблем машины Тьюринга , 1965], чтобы доказать, что Σ (3) = 6: для данного n , если S ( n ) известно, то все n -состояния Машины Тьюринга могут (в принципе) выполняться до S ( n ) шагов, после чего любая машина, которая еще не остановилась, никогда не остановится. В этот момент, наблюдая, какие машины остановились с наибольшим количеством единиц на ленте (т. Е. Занятые бобры), можно получить с их лент значение Σ ( n ). Подход, использованный Лином и Радо для случая n = 3, заключался в том, чтобы предположить, что S (3) = 21, а затем смоделировать все существенно разные трехпозиционные машины до 21 шага. Путем анализа поведения машин, которые не остановились в течение 21 шага, им удалось показать, что ни одна из этих машин никогда не остановится, тем самым доказав гипотезу о том, что S (3) = 21, и определив, что Σ (3) = 6 с помощью только что описанная процедура.
Неравенства, связывающие Σ и S, включают следующие (из [Ben-Amram, et al., 1996]), которые справедливы для всех n ≥ 1 :
и асимптотически улучшенная оценка (из [Ben-Amram, Petersen, 2002]): существует постоянная c , такая, что для всех n ≥ 2 ,
имеет тенденцию быть близкой к квадрату , и на самом деле многие машины дают меньше, чем .
Известные значения Σ и S
По состоянию на 2016 год значения функций для Σ ( n ) и S ( n ) точно известны только для n <5.
Текущий (по состоянию на 2018 год) чемпион занятых бобров в 5 штатах производит 4098 1 с, используя47 176 870 шагов (обнаружено Хайнером Марксеном и Юргеном Бантроком в 1989 г.), но остается 18 или 19 (возможно, менее 10, см. Ниже) машин с нестандартным поведением, которые, как считается, никогда не останавливаются, но которые не доказали, работать бесконечно. Скелет перечисляет 42 или 43 недоказанных машины, но 24 уже проверены. Остальные машины были смоделированы до 81,8 миллиарда шагов, но ни одна из них не остановилась. Дэниел Бриггс тоже испытал несколько машин. Другой источник говорит, что 98 машин остаются непроверенными. Есть анализ несогласных. Таким образом, вероятно, что Σ (5) = 4098 и S (5) = 47176870, но это остается недоказанным, и неизвестно, остались ли еще несогласованные (по состоянию на 2018 год). На данный момент рекордсмен из шести штатов производит более3,515 × 10 18 267 1 с (точно (25 × 4 30341 +23) / 9), используя более7,412 × 10 36 534 ступени (обнаружено Павлом Кропицем в 2010 г.). Как отмечалось выше, это двухсимвольные машины Тьюринга.
Простое расширение 6-конечного автомата приводит к 7-конечному автомату, который будет записывать более 10 10 10 1018 705 353 1 с на ленту, но, несомненно, есть гораздо более загруженные машины с 7 состояниями. Однако у других занятых охотников на бобров есть другие наборы машин.
Милтон Грин в своей статье 1964 года «Нижняя граница сигма-функции Радо для двоичных машин Тьюринга» построил набор машин Тьюринга, демонстрирующих, что
где ↑ - обозначение Кнута со стрелкой вверх, а A - функция Аккермана .
Таким образом
(с 3 3 3 = 7 625 597 484 987 членов в экспоненциальной башне), и
где число g 1 - огромное начальное значение в последовательности, определяющей число Грэма .
В 1964 году Милтон Грин разработал нижнюю границу для функции занятого бобра, которая была опубликована в трудах симпозиума IEEE 1964 года по теории коммутационных схем и логическому проектированию. Хайнер Марксен и Юрген Бантрок описали это как «нетривиальную (не примитивно рекурсивную) нижнюю границу». Эту нижнюю границу можно вычислить, но она слишком сложна, чтобы ее можно было сформулировать как единое выражение в терминах n. При n = 8 метод дает Σ (8) ≥ 3 × (7 × 3 92 - 1) / 2 ≈ 8,248 × 10 44 .
Из текущих нижних оценок можно вывести, что:
Напротив, лучшая текущая (по состоянию на 2018 год) нижняя граница Σ (6) равна 10 18 267 , что больше, чем нижняя граница, заданная формулой Грина, 3 3 = 27 (что для сравнения очень мало). Фактически, это намного больше, чем нижняя граница: 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , что является первой нижней оценкой Грина для Σ (8), а также намного больше, чем вторая нижняя граница: 3 × (7 × 3 92 −1) / 2.
Σ (7) таким же образом намного, намного больше, чем текущая общая нижняя граница 3 31 (почти 618 триллионов), поэтому вторая нижняя граница также очень, очень слабая.
Доказательство невычислимости S ( n ) и Σ ( n )
Предположим, что S ( n ) вычислимая функция, и пусть EvalS обозначает TM, вычисляющую S ( n ). Для ленты с n единицами она создаст на ленте S ( n ) единиц, а затем остановится. Пусть Clean обозначает машину Тьюринга, очищающую последовательность единиц, первоначально записанную на ленте. Пусть Double обозначает машину Тьюринга, вычисляющую функцию n + n . Для ленты с n единицами она создаст на ленте 2 n 1, а затем остановится. Создадим композицию Double | EvalS | Очистите и пусть n 0 будет количеством состояний этой машины. Пусть Create_n 0 обозначает машину Тьюринга, создающую n 0 единиц на изначально пустой ленте. Эта машина может быть сконструирована тривиальным образом, чтобы иметь n 0 состояний (состояние i записывает 1, перемещает голову вправо и переключается в состояние i + 1, за исключением состояния n 0 , которое останавливается). Обозначим через N сумму n 0 + n 0 .
Пусть BadS обозначает композицию Create_n 0 | Двойной | EvalS | Чистый . Обратите внимание, что у этой машины N состояний. Начиная с изначально пустой ленты, он сначала создает последовательность из n 0 единиц, а затем удваивает ее, создавая последовательность из N единиц. Затем BadS произведет на ленте S ( N ) 1, и, наконец, очистит все единицы, а затем остановится. Но фаза очистки будет продолжаться как минимум S ( N ) шагов, поэтому время работы BadS строго больше, чем S ( N ), что противоречит определению функции S ( n ).
Невычислимость Σ ( n ) доказывается аналогично. В приведенном выше доказательстве нужно заменить машину EvalS на EvalΣ и Clean with Increment - простой TM, ищущий на ленте первый 0 и заменяющий его на 1.
Невычислимость S ( n ) также может быть установлена путем ссылки на проблему остановки пустой ленты. Проблема остановки пустой ленты - это проблема принятия решения для любой машины Тьюринга, остановится она или нет при запуске с пустой ленты. Проблема остановки пустой ленты эквивалентна стандартной проблеме остановки, поэтому она также невычислима. Если бы S ( n ) было вычислимым, то мы могли бы решить проблему остановки пустой ленты, просто запустив любую заданную машину Тьюринга с n состояниями для S ( n ) шагов; если он все еще не остановился, он никогда не остановится. Итак, поскольку проблема остановки пустой ленты не вычислима, отсюда следует, что S ( n ) также должна быть невычислимой.
Обобщения
Для любой модели вычислений существуют простые аналоги занятого бобра. Например, обобщение машин Тьюринга с n состояниями и m символами определяет следующие обобщенные функции занятого бобра :
- Σ ( n , m ): наибольшее количество ненулевых символов, которое может напечатать машина с n- состояниями, m- символами, запущенными на первоначально пустой ленте перед остановкой, и
- S ( n , m ): наибольшее количество шагов, предпринятых машиной с n- состояниями, m- символами, запущенными на изначально пустой ленте перед остановкой.
Например, найденная до сих пор самая продолжительная трехсимвольная машина с 3 состояниями работает 119 112 334 170 342 540 шагов до остановки. Самая продолжительная машина с 6 состояниями и 2 символами, которая имеет дополнительное свойство реверсирования значения ленты на каждом шаге, производит6147 1 с после47 339 970 шагов. Итак, S RTM (6) ≥47 339 970 и Σ RTM (6) ≥6147 .
Возможно дальнейшее обобщение функции занятого бобра, расширив ее до более чем одного измерения.
Точно так же мы могли бы определить аналог функции Σ для регистровых машин как наибольшее число, которое может присутствовать в любом регистре при остановке для данного количества инструкций.
Точные значения и нижние границы
В следующей таблице перечислены точные значения и некоторые известные нижние границы для S ( n , m ) и Σ ( n , m ) для обобщенных задач занятого бобра. Примечание: записи, перечисленные как "?" ограничены снизу максимумом всех записей слева и сверху. Эти машины либо не исследовались, либо были впоследствии заменены более мелкими машинами.
Машины Тьюринга, которые достигают этих значений, доступны на веб-странице Паскаля Мишеля . Каждый из этих веб-сайтов также содержит некоторый анализ машин Тьюринга и ссылки на доказательства точных значений.
Значения S ( n , m ) пм2-состояние 3-состояние 4-состояние 5-состояние 6-состояние 7-состояние 2 символа 6 21 год 107 47 176 870 ? > 7,4 × 10 36 534 > 10 10 10 1018 705 353 3 символа 38 ≥ 119 112 334 170 342 540 > 1,0 × 10 14 072 ? ? ? 4 символа ≥ 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5-значное > 1,9 × 10 704 ? ? ? ? ? 6-значное > 2,4 × 10 9866 ? ? ? ? ? Значения Σ ( n , m ) пм2-состояние 3-состояние 4-состояние 5-состояние 6-состояние 7-состояние 2 символа 4 6 13 4098 ? > 3,5 × 10 18 267 > 10 10 10 1018 705 353 3 символа 9 ≥ 374 676 383 > 1,3 × 10 7036 ? ? ? 4 символа ≥ 2050 г. > 3,7 × 10 6518 ? ? ? ? 5-значное > 1,7 × 10 352 ? ? ? ? ? 6-значное > 1,9 × 10 4933 ? ? ? ? ?
Недетерминированные машины Тьюринга
| п | шаги | состояния |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
Проблема может быть распространена на недетерминированные машины Тьюринга путем поиска системы с наибольшим количеством состояний во всех ветвях или ветви с наибольшим количеством шагов. Вопрос о том, остановится ли данный NDTM, по-прежнему не сводится к вычислению, и вычисления, необходимые для поиска занятого бобра с NDTM, значительно больше, чем в детерминированном случае, поскольку необходимо учитывать несколько ветвей. Для системы с 2 состояниями и 2 цветами с p случаями или правилами таблица справа дает максимальное количество шагов перед остановкой и максимальное количество уникальных состояний, созданных NDTM.
Приложения
Помимо постановки довольно сложной математической игры , функции занятого бобра предлагают совершенно новый подход к решению чисто математических задач. Многие открытые проблемы математики теоретически, но не на практике, могут быть решены систематическим образом, учитывая значение S ( n ) для достаточно большого n .
Рассмотрим любую гипотезу , которая может быть опровергнута через контрпример среди счетного числа случаев (например , Гольдбаха - гипотезы ). Напишите компьютерную программу, которая последовательно проверяет эту гипотезу на предмет увеличения значений. В случае гипотезы Гольдбаха мы будем рассматривать каждое четное число ≥ 4 последовательно и проверять, является ли оно суммой двух простых чисел. Предположим, эта программа моделируется на машине Тьюринга с n состояниями. Если он находит контрпример (четное число ≥ 4, которое не является суммой двух простых чисел в нашем примере), он останавливается и указывает на это. Однако, если гипотеза верна, наша программа никогда не остановится. (Эта программа останавливается, только если находит контрпример.)
Теперь эта программа моделируется машиной Тьюринга с n состояниями, поэтому, если мы знаем S ( n ), мы можем решить (за конечный промежуток времени), остановится ли она когда-либо, просто запустив машину столько шагов. И если после S ( n ) шагов машина не останавливается, мы знаем, что она никогда не остановится, и, следовательно, нет никаких контрпримеров к данной гипотезе (т.е. нет четных чисел, не являющихся суммой двух простых чисел). Это подтвердит, что гипотеза верна.
Таким образом, конкретные значения (или верхние границы) для S ( n ) могут использоваться для систематического решения многих открытых проблем математики (теоретически). Однако текущие результаты по проблеме занятого бобра показывают, что это нецелесообразно по двум причинам:
- Чрезвычайно сложно доказать значения для функции занятого бобра (и функции максимального сдвига). Это было доказано только для чрезвычайно маленьких машин с менее чем пятью состояниями, в то время как для создания полезной машины, предположительно, потребуется не менее 20-50 состояний. Кроме того, каждое известное точное значение S ( n ) было доказано путем перечисления каждой машины Тьюринга с n состояниями и доказательства того, останавливается ли каждая из них. Чтобы это действительно было полезно, нужно было бы вычислить S ( n ) каким-либо менее прямым методом.
- Но даже если найти лучший способ вычисления S ( n ), значения функции занятого бобра (и функции максимального сдвига) станут очень большими и очень быстро. S (6)> 1036 534 уже требует специального ускорения на основе шаблонов, чтобы можно было смоделировать до завершения. Точно так же мы знаем, что S (10)> Σ (10)> 3 ↑↑↑ 3 - это гигантское число, а S (17)> Σ (17)> G, где G - число Грэма, - огромное число. Таким образом, даже если бы мы знали, скажем, S (30), было бы совершенно неразумно запускать какую-либо машину с таким количеством шагов. В известной части Вселенной недостаточно вычислительных мощностей, чтобы выполнять дажеоперации S (6) напрямую.
Известные примеры
Была построена двоичная машина Тьюринга с 748 состояниями, которая останавливается, если ZFC несовместима. Была построена машина Тьюринга с 744 состояниями, которая останавливается, если гипотеза Римана неверна. Была построена машина Тьюринга с 43 состояниями, которая останавливается, если гипотеза Гольдбаха ложна, и машина с 27 состояниями для этой гипотезы была предложена, но еще не проверена.
Была построена машина Тьюринга с 15 состояниями, которая останавливается тогда и только тогда, когда следующая гипотеза, сформулированная Полом Эрдёшем в 1979 году, неверна: для всех n> 8 существует по крайней мере одна цифра 2 в представлении 2 n по основанию 3 .
Примеры
Это таблицы правил для машин Тьюринга, которые порождают Σ (1) и S (1), Σ (2) и S (2), Σ (3) (но не S (3)), Σ (4) и S (4) и наиболее известная нижняя оценка для Σ (5) и S (5), а также Σ (6) и S (6). Для других визуализаций
В таблицах столбцы представляют текущее состояние, а строки представляют текущий символ, считанный с ленты. Каждая запись в таблице представляет собой строку из трех символов, указывающую символ для записи на ленту, направление движения и новое состояние (в указанном порядке). Состояния останова показано как H .
Каждая машина начинается в состоянии A с бесконечной ленты, содержащей все нули. Таким образом, начальный символ, считанный с ленты, равен 0.
Ключевой результат: (начинается с позиции линиями , проведенными сверху , останавливается в положении подчеркнуты )
Занятый бобер с 1 состоянием, 2 символа А 0 1R H 1 (не используется)
Результат: 0 0 1 0 0 (1 шаг, всего одна "1")
2 состояния, 2 символа занятого бобра А B 0 1R B 1L А 1 1L B 1R H
Результат: 0 0 1 1 1 1 0 0 (6 шагов, всего четыре единицы)
Занятый бобер с 3 состояниями, 2 символа А B C 0 1R B 0R C 1L C 1 1R H 1R B 1L А
Результат: 0 0 1 1 1 1 1 1 0 0 (14 шагов, всего шесть единиц).
В отличии от предыдущих машин, это один занят бобер только для Е, но не для S . ( S (3) = 21).
Занятый бобер с 4 состояниями, 2 символа А B C D 0 1R B 1L А 1R H 1R D 1 1L B 0L C 1L D 0R A
Результат: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 шагов, всего тринадцать единиц)
текущий лучший претендент с 5 состояниями и 2 символами (возможно, занятый бобёр) А B C D E 0 1R B 1R C 1R D 1L А 1R H 1 1L C 1R B 0L E 1L D 0L A
Результат: 4098 "1" с 8191 "0" с вкраплениями 47 176 870 шагов.
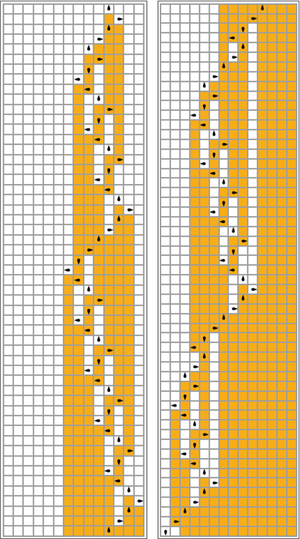
Обратите внимание на изображение справа, насколько это решение качественно похоже на эволюцию некоторых клеточных автоматов .
Текущий лучший претендент на 6 состояний, 2 символа А B C D E F 0 1R B 1R C 1L D 1R E 1L А 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
Результат: ≈3,515 × 10 18267 "1" с за ≈7,412 × 10 36534 шагов.
Визуализации
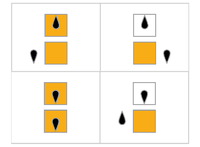
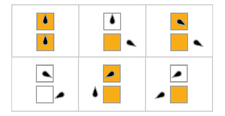
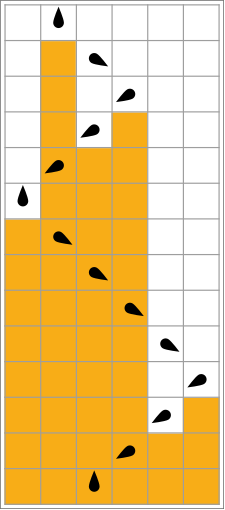
В следующей таблице правила для каждого занятого бобра (максимизация Σ) представлены визуально: оранжевые квадраты соответствуют «1» на ленте, а белые - «0». Положение головы обозначено черным овалом, а ориентация головы представляет состояние. Отдельные ленты выкладываются горизонтально, с течением времени по вертикали. Состояние остановки представлено правилом, которое отображает одно состояние на себя (голова не двигается).
Смотрите также
Примечания
- ^ a b Radó, Тибор (май 1962 г.). «О невычислимых функциях» (PDF) . Технический журнал Bell System . 41 (3): 877–884. DOI : 10.1002 / j.1538-7305.1962.tb00480.x .
- ^ Чайтин (1987)
- ^ Адам Yedidia и Скотт Аронсон (май 2016). Относительно небольшая машина Тьюринга, поведение которой не зависит от теории множеств (технический отчет). Массачусетский технологический институт. arXiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
- ^ Арон, Джейкоб. «Эта машина Тьюринга должна работать вечно, если математика не ошибается» . Проверено 25 сентября 2016 .
- ^ a b Версия от 3 мая содержала 7918 утверждений: «8000-е число занятых бобров ускользает от теории множеств ZF» . Штетл-оптимизированный блог . 2016-05-03 . Проверено 25 сентября 2016 .
- ^ a b c "Три объявления" . Штетл-оптимизированный блог . 2016-05-03 . Проверено 27 апреля 2018 .
- ^ "GitHub - sorear / metamath-turing-machines: счетчики для проверки Metamath и другие вещи" . 2019-02-13.
- ^ "Занятый Бобровый рубеж" (PDF) .
- ^ "Скелетная страница для проблемы Занятого бобра" . skelet.ludost.net .
- ↑ Тьюринг: проект по завершению «Занятого бобра из 5»
- ^ "Проблема занятого бобра: НОВАЯ АТАКА ТЫСЯЧЕЛЕТИЯ" .
- ^ a b Вольфрам, Стивен (4 февраля 2021 г.). «Многосторонние машины Тьюринга» . www.wolframphysics.org .
- ^ Хайтина 1987
- ^ Ллойд 2001. Вычислительная мощность Вселенной .
- ^ a b c Павлус, Джон (10 декабря 2020 г.). «Как самые медленные компьютерные программы освещают фундаментальные пределы математики» . Журнал Quanta . Проверено 11 декабря 2020 .
- ^ Тристан Стериным и Дэмиен Woods (июль 2021). По твердости знания занятого бобра значения BB (15) и BB (5,4) (Технический отчет). Университет Мейнута. arXiv : 2107.12475 .
- ^ ЭРДЁШ, Павел (1979). «Некоторые нестандартные задачи теории чисел» . Математика. Mag. 52 (2): 67–70. DOI : 10.1080 / 0025570X.1979.11976756 .
- ^ Лин, Шэнь; Радо, Тибор (апрель 1965 г.). «Компьютерные исследования проблем машины Тьюринга» . Журнал ACM . 12 (2): 196–212. DOI : 10.1145 / 321264.321270 . S2CID 17789208 .
использованная литература
-
Радо, Тибор (май 1962 г.). «О невычислимых функциях» (PDF) . Технический журнал Bell System . 41 (3): 877–884. DOI : 10.1002 / j.1538-7305.1962.tb00480.x .
- Именно здесь Радо впервые определил проблему занятого бобра и доказал, что она невычислима и растет быстрее, чем любая вычислимая функция.
-
Линь, Шэнь; Радо, Тибор (апрель 1965 г.). "Компьютерные исследования проблем машины Тьюринга" . Журнал ACM . 12 (2): 196–212. DOI : 10.1145 / 321264.321270 . S2CID 17789208 .
- Результаты этой статьи уже частично были опубликованы в докторской диссертации Линь в 1963 году под руководством Радо. Лин и Радо доказывают, что Σ (3) = 6 и S (3) = 21, доказывая, что все машины Тьюринга с 3 состояниями и 2 символами, которые не останавливаются в пределах 21 шага, никогда не остановятся. (Большинство из них автоматически проверяется компьютерной программой, однако 40 проверяются человеком.)
-
Брэди, Аллен Х. (апрель 1983 г.). «Определение значения невычислимой функции Радо Σ ( k ) для четырехуровневых машин Тьюринга» . Математика вычислений . 40 (162): 647–665. DOI : 10.1090 / S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Брэди доказывает, что Σ (4) = 13 и S (4) = 107. Брэди определяет две новые категории для неизменяющихся машин Тьюринга с 3 состояниями и 2 символами: рождественские елки и счетчики. Он использует компьютерную программу, чтобы доказать, что все машины, кроме 27, которые выполняют 107 шагов, являются вариантами рождественских елок и счетчиков, которые, как можно доказать, работают бесконечно. Последние 27 машин (так называемые «упорные») лично Брэди лично осмотрели их, чтобы не останавливаться.
-
Махлин, Рона; Стаут, Квентин Ф. (июнь 1990 г.). «Сложное поведение простых машин» . Physica D: нелинейные явления . 42 (1–3): 85–98. Bibcode : 1990PhyD ... 42 ... 85M . DOI : 10.1016 / 0167-2789 (90) 90068-Z . ЛВП : 2027,42 / 28528 .
- Махлин и Стаут описывают проблему занятого бобра и многие методы, используемые для поиска занятого бобра (которые они применяют к машинам Тьюринга с 4-мя состояниями и 2-значными символами, тем самым подтверждая доказательство Брэди). Они предлагают, как оценить вариант вероятности остановки (Ω) Чайтина.
-
Марксен, Хайнер; Buntrock, Юрген (февраль 1990 г.). «Нападение на занятого бобра 5» . Бюллетень EATCS . 40 : 247–251. Архивировано 9 октября 2006 года . Проверено 19 января 2020 .
- Марксен и Бантрок демонстрируют, что Σ (5) ≥ 4098 и S (5) ≥ 47 176 870 и подробно опишите метод, который они использовали, чтобы найти эти машины, и докажите, что многие другие никогда не остановятся.
-
Грин, Милтон В. (1964). Нижняя граница сигма-функции Rado для двоичных машин Тьюринга . 1964 Труды пятого ежегодного симпозиума по теории коммутационных цепей и логическому проектированию . С. 91–94. DOI : 10.1109 / SWCT.1964.3 .
- Грин рекурсивно конструирует машины для любого количества состояний и предоставляет рекурсивную функцию, которая вычисляет их оценку (вычисляет σ), тем самым обеспечивая нижнюю границу для Σ. Рост этой функции сравним с ростом функции Аккермана .
-
Дьюдни, Александр К. (1984). «Компьютерная ловушка для занятого бобра, самая трудолюбивая машина Тьюринга». Scientific American . 251 (2): 10–17.
- Оживленные бобровые программы описаны Александром Дьюдни в Scientific American , август 1984 г., страницы 19–23, а также март 1985 г., стр. 23 и апреля 1985 г. с. 30 .
- Чайтин, Грегори Дж. (1987). «Вычисление функции занятого бобра» (PDF) . In Cover, TM; Гопинатх, Б. (ред.). Открытые проблемы в коммуникации и вычислениях . Springer. С. 108–112. ISBN 978-0-387-96621-2.
-
Брэди, Аллен Х. (1995). «Оживленная игра бобра и смысл жизни». В Херкене, Рольф (ред.). Универсальная машина Тьюринга: обзор за полвека (2-е изд.). Вена, Нью-Йорк: Springer-Verlag. С. 237–254. ISBN 978-3-211-82637-9.
- При этом Брэди (известный в четырех штатах) описывает некоторую историю зверя и называет его погоню «Занятой бобровой игрой». Он описывает другие игры (например, клеточные автоматы и «Игру жизни» Конвея ). Особый интерес представляет «Игра занятого бобра в двух измерениях» (стр. 247). С 19 ссылками.
-
Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов . Нью-Йорк: Вили. ISBN 978-0-471-08848-6.
- См. Главу 9, Машины Тьюринга. Сложная книга, рассчитанная на инженеров-электриков и технических специалистов. Обсуждает рекурсию, частичную рекурсию со ссылкой на машины Тьюринга, проблему остановки. Ссылка в Бут приписывает Rado занятого бобра. Бут также определяет проблему занятого бобра Rado в «домашних задачах» 3, 4, 5, 6 главы 9, с. 396. Задача 3 состоит в том, чтобы «показать, что проблема занятого бобра неразрешима ... для всех значений n».
-
Бен-Амрам, AM; Julstrom, BA; Цвик, У. (1996). «Заметка о занятых бобрах и других существах» . Математическая теория систем . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . DOI : 10.1007 / BF01192693 . S2CID 30937913 .
- Границы между функциями Е и S .
-
Бен-Амрам, AM; Петерсен, Х. (2002). «Улучшенные границы для функций, связанных с занятыми бобрами». Теория вычислительных систем . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . DOI : 10.1007 / s00224-001-1052-0 . S2CID 10429773 .
- Улучшенные границы.
-
Lafitte, G .; Папазян, К. (июнь 2007 г.). «Ткань малых машин Тьюринга». Вычисления и логика в реальном мире, Труды Третьей конференции по вычислимости в Европе . С. 219–227. CiteSeerX 10.1.1.104.3021 .
- Эта статья содержит полную классификацию машин Тьюринга с 2 состояниями и 3 символами и, таким образом, доказательство для (2, 3) занятого бобра: Σ (2, 3) = 9 и S (2, 3) = 38.
- Boolos, George S .; Берджесс, Джон П .; Джеффри, Ричард С. (2007). Вычислимость и логика (Пятое изд.). Издательство Кембриджского университета. ISBN 978-0-521-87752-7.
-
Кропиц, Павел (2010). Problém Busy Beaver (диплом бакалавра) (на словацком языке). Карлов университет в Праге.
- Это описание идей, алгоритмов и их реализации, с описанием экспериментов, исследующих машины Тьюринга с 5 и 6 состояниями путем параллельного запуска на 31 4-ядерном компьютере и, наконец, лучшие результаты для TM с 6 состояниями.
внешние ссылки
- Страница Хайнера Марксена , который вместе с Юргеном Бантроком нашел вышеупомянутые записи для машины Тьюринга с 5 и 6 состояниями.
- Исторический обзор занятых бобрами результатов Паскаля Мишеля, который также содержит лучшие результаты и некоторый анализ.
- Определение класса RTM - Обратные машины Тьюринга, простой и сильный подкласс TM.
- " Атака тысячелетия " в Rensselaer RAIR Lab по проблеме занятого бобра. Эта попытка установила несколько новых рекордов и установила несколько значений для четверной формализации.
- Архив веб - сайта и форум Дэниела Бриггса для решения проблемы занятого бобра с 5 состояниями и 2 символами, основанный на списке нерегулярных машин Skelet (Георгий Георгиев).
- Ааронсон, Скотт (1999), Кто может назвать самое большое число?
- Вайсштейн, Эрик В. «Занятый бобер» . MathWorld .
- Машины Тьюринга занятого бобра - компьютерфил
- Паскаль Мишель. Конкурс занятых бобров: исторический обзор . 70 страниц. 2017. <hal-00396880v5>