Неравенство треугольника - Triangle inequality

Три примера неравенства треугольника для треугольников со сторонами длины

x

,

y

,

z

. В верхнем примере показан случай, когда

z

намного меньше суммы

x + y

двух других сторон, а в нижнем примере показан случай, когда сторона

z

лишь немного меньше

x + y

.

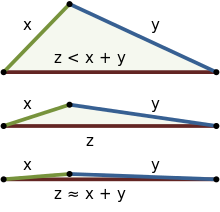
В математике , то неравенство треугольника гласит , что для любого треугольника , сумма длин любых двух сторон должна быть больше или равна длине оставшейся части. Это утверждение допускает включение вырожденных треугольников , но некоторые авторы, особенно те, кто пишет об элементарной геометрии, исключают эту возможность, тем самым опуская возможность равенства. Если $x$ , $y$ и $z$ - длины сторон треугольника, причем ни одна из сторон не больше $z$ , то неравенство треугольника гласит, что

{\ Displaystyle г \ Leq х + у,}

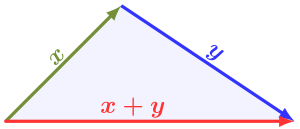
с равенством только в вырожденном случае треугольника нулевой площади. В евклидовой геометрии и некоторых других геометриях неравенство треугольника является теоремой о расстояниях, и оно записывается с использованием векторов и векторных длин ( норм ):

{\ Displaystyle \ | \ mathbf {x} + \ mathbf {y} \ | \ leq \ | \ mathbf {x} \ | + \ | \ mathbf {y} \ |,}

где длина $z$ третьей стороны заменена векторной суммой $x + y$ . Когда $x$ и $y$ являются действительными числами , их можно рассматривать как векторы в $R 1$ , а неравенство треугольника выражает взаимосвязь между абсолютными значениями .

В евклидовой геометрии для прямоугольных треугольников неравенство треугольника является следствием теоремы Пифагора , а для общих треугольников - следствием закона косинусов , хотя его можно доказать и без этих теорем. Неравенство можно интуитивно рассматривать как в $R 2, так$ и в $R 3$ . На рисунке справа показаны три примера, начиная с явного неравенства (вверху) и приближаясь к равенству (внизу). В евклидовом случае равенство происходит только в том случае, если треугольник имеет угол $180 °$ и два угла $0 °$ , что делает три вершины коллинеарными , как показано в нижнем примере. Таким образом, в евклидовой геометрии кратчайшее расстояние между двумя точками - прямая линия.

В сферической геометрии кратчайшее расстояние между двумя точками - это дуга большого круга , но неравенство треугольника выполняется при условии, что расстояние между двумя точками на сфере равно длине небольшого сегмента сферической линии (т. Е. один с центральным углом в $[0, π]$ ) с этими концами.

Неравенство треугольника является определяющим свойством из норм и мер расстояния . Это свойство должно быть установлено в качестве теоремы для любой функции , предложенной для таких целей для каждого конкретного пространства: например, пробела , таких как действительные числа , евклидовы пространства , в л ^р пространства ( $р \geq 1$ ), а также внутренние пространства продукции .

Евклидова геометрия

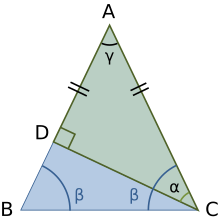
Конструкция Евклида для доказательства неравенства треугольника для плоской геометрии.

Евклид доказал неравенство треугольника для расстояний в плоской геометрии, используя конструкцию на рисунке. Начиная с треугольника $ABC$ , строится равнобедренный треугольник, одна сторона которого берется за $BC,$ а другой равный отрезок $BD$ проходит вдоль стороны $AB$ . Затем утверждается, что угол $β > α$ , поэтому сторона $AD > AC$ . Но $AD = AB + BD = AB + BC,$ поэтому сумма сторон $AB + BC > AC$ . Это доказательство появляется в Книге 1 предложения 20 Евклида «Элементы» .

Математическое выражение ограничения на сторонах треугольника

Для правильного треугольника неравенство треугольника, как сказано на словах, буквально переводится в три неравенства (при условии, что правильный треугольник имеет длину сторон $a$ , $b$ , $c$ , которые все положительны, и исключает вырожденный случай нулевой площади):

{\ displaystyle a + b> c, \ quad b + c> a, \ quad c + a> b.}

Более сжатая форма этой системы неравенств может быть представлена следующим образом:

{\ displaystyle | ab | <c <a + b.}

Другой способ заявить об этом -

{\ Displaystyle \ макс (a, b, c) <a + b + c- \ max (a, b, c)}

подразумевая

{\ Displaystyle 2 \ макс (a, b, c) <a + b + c}

и, таким образом, длина самой длинной стороны меньше полупериметра .

Математически эквивалентная формулировка состоит в том, что площадь треугольника со сторонами a , b , c должна быть действительным числом больше нуля. Формула Герона для площади:

{\ displaystyle {\ begin {align} 4 \ cdot {\ text {area}} & = {\ sqrt {(a + b + c) (- a + b + c) (a-b + c) (a + bc)}} \\ & = {\ sqrt {-a ^ {4} -b ^ {4} -c ^ {4} + 2a ^ {2} b ^ {2} + 2a ^ {2} c ^ { 2} + 2b ^ {2} c ^ {2}}}. \ End {выравнивается}}}

В терминах любого выражения площади неравенство треугольника, наложенное со всех сторон, эквивалентно условию, что выражение под знаком квадратного корня является действительным и больше нуля (так что выражение площади является действительным и больше нуля).

Неравенство треугольника дает еще два интересных ограничения для треугольников со сторонами a, b, c , где a ≥ b ≥ c и является золотым сечением , так как ${\ displaystyle \ phi}$

{\ displaystyle 1 <{\ frac {a + c} {b}} <3}

{\ displaystyle 1 \ leq \ min \ left ({\ frac {a} {b}}, {\ frac {b} {c}} \ right) <\ phi.}

Прямоугольный треугольник

Равнобедренный треугольник с равными сторонами

AB = AC,

разделенный на два прямоугольных треугольника высотой, рассчитанной из одного из двух углов основания.

В случае прямоугольных треугольников неравенство треугольника специализируется на утверждении, что гипотенуза больше любой из двух сторон и меньше их суммы.

Вторая часть этой теоремы уже установлена выше для любой стороны любого треугольника. Первая часть устанавливается с помощью нижнего рисунка. На рисунке рассмотрим прямоугольный треугольник $АЦП$ . Построен равнобедренный треугольник $ABC$ с равными сторонами $AB = AC$ . Из треугольника постулата , то углы в прямоугольном треугольнике $ADC$ удовлетворяет:

{\ Displaystyle \ альфа + \ гамма = \ пи / 2 \.}

Точно так же в равнобедренном треугольнике $ABC$ углы удовлетворяют следующим условиям:

{\ Displaystyle 2 \ бета + \ гамма = \ пи \.}

Следовательно,

{\ Displaystyle \ альфа = \ пи / 2- \ гамма, \ \ mathrm {в то время как} \ \ бета = \ пи / 2- \ гамма / 2 \,}

и так, в частности,

{\ Displaystyle \ альфа <\ бета \.}

Это означает, что сторона $AD,$ противоположная углу $α$ , короче, чем сторона $AB,$ противоположная большему углу $β$ . Но $AB = AC$ . Следовательно:

{\ displaystyle {\ overline {\ mathrm {AC}}}> {\ overline {\ mathrm {AD}}} \.}

Аналогичная конструкция показывает $AC > DC$ , что доказывает теорему.

Альтернативное доказательство (также основанное на постулате треугольника) заключается в рассмотрении трех положений точки $B$ : (i) как изображено (что необходимо доказать), или (ii) $B,$ совпадающей с $D$ (что означало бы, что в равнобедренном треугольнике было два прямые углы в качестве основных углов плюс угол при вершине $γ$ , что нарушит постулат треугольника ), или, наконец, (iii) $B$ внутри прямоугольного треугольника между точками $A$ и $D$ (в этом случае угол $ABC$ является внешним углом прямоугольного треугольника $BDC$ и, следовательно, больше, чем $π / 2$ , что означает, что другой угол основания равнобедренного треугольника также больше, чем $π / 2,$ и их сумма превышает $π$ в нарушение постулата треугольника).

Эта теорема, устанавливающая неравенства, уточняется теоремой Пифагора до того, что квадрат длины гипотенузы равен сумме квадратов двух других сторон.

Примеры использования

Рассмотрим треугольник, стороны которого находятся в арифметической прогрессии, и пусть стороны равны $a$ , $a + d$ , $a + 2 d$ . Тогда неравенство треугольника требует, чтобы

{\ displaystyle 0 <a <2a + 3d}

{\ displaystyle 0 <a + d <2a + 2d}

{\ displaystyle 0 <a + 2d <2a + d.}

Для удовлетворения всех этих неравенств требуется

{\ displaystyle a> 0 {\ text {and}} - {\ frac {a} {3}} <d <a.}

Когда $d$ выбирается так, что $d = a / 3$ , он генерирует прямоугольный треугольник, который всегда похож на тройку Пифагора со сторонами $3$ , $4$ , $5$ .

Теперь рассмотрим треугольник, стороны которого находятся в геометрической прогрессии, и пусть стороны равны $a$ , $ar$ , $ar 2$ . Тогда неравенство треугольника требует, чтобы

{\ Displaystyle 0 <а <ар + ар ^ {2}}

{\ Displaystyle 0 <ар <а + ар ^ {2}}

{\ displaystyle 0 <ar ^ {2} <a + ar.}

Первое неравенство требует $a > 0$ ; следовательно, его можно разделить и устранить. При $a > 0$ среднее неравенство требует только $r > 0$ . Это оставляет первое и третье неравенства, которые должны удовлетворять

{\ displaystyle {\ begin {align} r ^ {2} + r-1 & {}> 0 \\ r ^ {2} -r-1 & {} <0. \ end {align}}}

Первое из этих квадратичных неравенств требует, чтобы $r находилось$ в диапазоне, превышающем значение положительного корня квадратного уравнения $r 2 + r - 1 = 0$ , то есть $r > φ - 1,$ где $φ$ - золотое сечение . Второе квадратное неравенство требует, чтобы $r находилось$ в диапазоне от 0 до положительного корня квадратного уравнения $r 2 - r - 1 = 0$ , то есть $0 < r < φ$ . Комбинированные требования приводят к тому, что $r$ ограничивается диапазоном

{\ displaystyle \ varphi -1 <r <\ varphi \, {\ text {and}} a> 0.}

Когда $r$ выбирается обычное отношение так, что $r = \sqrt φ,$ получается прямоугольный треугольник, который всегда похож на треугольник Кеплера .

Обобщение на любой многоугольник

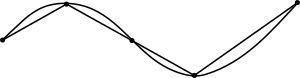
Неравенство треугольника может быть расширено математической индукцией на произвольные многоугольные пути, показывая, что общая длина такого пути не меньше, чем длина прямой линии между его конечными точками. Следовательно, длина любой стороны многоугольника всегда меньше суммы длин сторон других многоугольников.

Пример обобщенного неравенства многоугольника для четырехугольника

Рассмотрим четырехугольник, стороны которого расположены в геометрической прогрессии, и пусть стороны равны $a$ , $ar$ , $ar 2$ , $ar 3$ . Тогда обобщенное неравенство многоугольника требует, чтобы

{\ displaystyle 0 <a <ar + ar ^ {2} + ar ^ {3}}

{\ displaystyle 0 <ar <a + ar ^ {2} + ar ^ {3}}

{\ displaystyle 0 <ar ^ {2} <a + ar + ar ^ {3}}

{\ displaystyle 0 <ar ^ {3} <a + ar + ar ^ {2}.}

Эти неравенства при $a > 0$ сводятся к следующему

{\ displaystyle r ^ {3} + r ^ {2} + r-1> 0}

{\ displaystyle r ^ {3} -r ^ {2} -r-1 <0.}

Полиномы в левой части этих двух неравенств имеют корни, которые являются константой трибоначчи и обратной ей. Следовательно, $r$ ограничено диапазоном $1 / t < r < t,$ где $t$ - постоянная трибоначчи.

Отношения с кратчайшими путями

Длина дуги кривой определяется как наименьшая верхняя граница длин полигональных аппроксимаций.

Это обобщение можно использовать, чтобы доказать, что кратчайшая кривая между двумя точками в евклидовой геометрии является прямой линией.

Никакой многоугольный путь между двумя точками не короче линии между ними. Это означает, что никакая кривая не может иметь длину дуги меньше, чем расстояние между ее конечными точками. По определению длина дуги кривой - это наименьшая верхняя граница длин всех полигональных аппроксимаций кривой. Результат для многоугольных путей показывает, что прямая линия между конечными точками является самой короткой из всех многоугольных приближений. Поскольку длина дуги кривой больше или равна длине каждого полигонального приближения, сама кривая не может быть короче прямой линии.

Converse

Верно и обратное утверждение теоремы о неравенстве треугольника: если три действительных числа таковы, что каждое меньше суммы других, то существует треугольник с этими числами в качестве длин сторон и с положительной площадью; и если одно число равно сумме двух других, существует вырожденный треугольник (то есть с нулевой площадью) с этими числами в качестве длин сторон.

В любом случае, если длины сторон равны a, b, c, мы можем попытаться разместить треугольник в евклидовой плоскости, как показано на диаграмме. Нам нужно доказать, что существует действительное число h, согласованное со значениями a, b и c , и в этом случае этот треугольник существует.

Треугольник с высотой

h

разрезает основание

c

на

d + (c - d)

.

По теореме Пифагора мы имеем $b 2 = h 2 + d 2$ и $a 2 = h 2 + (c - d) 2$ согласно рисунку справа. Вычитание этих значений дает $a 2 - b 2 = c 2 - 2 кд$ . Это уравнение позволяет нам выразить $d$ через стороны треугольника:

{\ displaystyle d = {\ frac {-a ^ {2} + b ^ {2} + c ^ {2}} {2c}}.}

Для высоты треугольника $h 2 = b 2 - d 2$ . Заменяя $d$ на формулу, приведенную выше, мы имеем

{\ displaystyle h ^ {2} = b ^ {2} - \ left ({\ frac {-a ^ {2} + b ^ {2} + c ^ {2}} {2c}} \ right) ^ { 2}.}

Чтобы действительное число h удовлетворяло этому требованию, оно должно быть неотрицательным: ${\ displaystyle h ^ {2}}$

{\ displaystyle b ^ {2} - \ left ({\ frac {-a ^ {2} + b ^ {2} + c ^ {2}} {2c}} \ right) ^ {2} \ geq 0, }

{\ displaystyle \ left (b - {\ frac {-a ^ {2} + b ^ {2} + c ^ {2}} {2c}} \ right) \ left (b + {\ frac {-a ^ { 2} + b ^ {2} + c ^ {2}} {2c}} \ right) \ geq 0,}

{\ displaystyle \ left (a ^ {2} - (bc) ^ {2}) ((b + c) ^ {2} -a ^ {2} \ right) \ geq 0,}

{\ Displaystyle (a + bc) (a-b + c) (b + c + a) (b + ca) \ geq 0,}

{\ displaystyle (a + bc) (a + cb) (b + ca) \ geq 0,}

которое выполняется, если неравенство треугольника выполняется для всех сторон. Следовательно, действительно существует действительное число h, соответствующее сторонам a, b, c , и треугольник существует. Если каждое неравенство треугольника выполняется строго , h > 0 и треугольник невырожден (имеет положительную площадь); но если одно из неравенств выполняется с равенством, то есть h = 0, треугольник вырожден.

Обобщение на более высокие измерения

Площадь треугольной грани тетраэдра меньше или равна сумме площадей трех других треугольных граней. В более общем смысле , в евклидове пространства гиперплощади с $(п - 1)$ - фаска из с $п$ - симплекс (т.е. треугольник ( $п = 2$ ), тетраэдр ( $п = 3$ ), пентатоп ( $п = 4$ ) и т.д.) меньше или равно сумме гиперпространств других $n$ граней. Подобно тому, как неравенство треугольника обобщается на неравенство многоугольника - см. Выше, - неравенство для симплекса любой размерности обобщается на многогранник любой размерности: гиперплощадь любой грани многогранника меньше или равна сумме гиперпространств многогранника остальные грани.

Отметим, что неравенство треугольника не всегда подразумевает тетраэдрическое неравенство в следующем смысле. Предположим, что имеется четыре точки и попарные расстояния между ними равны $AB = BC = CA = 7$ и $AZ = BZ = CZ = 4$ . Каждая тройка этих точек удовлетворяет неравенству треугольника, но оказывается, что четыре точки не могут быть вершинами тетраэдра, в данном случае с одним равносторонним треугольником 7-7-7 и тремя равнобедренными треугольниками 7-4-4 в качестве граней. Мы знаем это, потому что тетраэдрическое неравенство не выполняется: площадь треугольника $ABC$ была бы приблизительно 21,22 по формуле Герона , и это не меньше суммы площадей трех других треугольников, каждый из которых равен примерно 6,78 по формуле Герона. .

Нормированное векторное пространство

Неравенство треугольника для норм векторов.

В нормированном векторном пространстве $V$ одним из определяющих свойств нормы является неравенство треугольника:

{\ Displaystyle \ | х + у \ | \ Leq \ | х \ | + \ | у \ | \ quad \ forall \, х, у \ в V}

то есть норма суммы двух векторов не больше суммы норм двух векторов. Это также называется субаддитивностью . Чтобы любая предлагаемая функция работала как норма, она должна удовлетворять этому требованию. Если нормированное пространство евклидово или, в более общем смысле, строго выпукло , то тогда и только тогда треугольник, образованный $x$ , $y$ и $x$ $+$ $y$ , вырожден, то есть $x$ и $y$ находятся на одном луче, т. Е. $x$ $= 0$ или $y$ $= 0$ , или $x$ $=$ $α y$ для некоторого $α$ $> 0$ . Это свойство характеризует строго выпуклые нормированные пространства, такие как $ℓ$ $p-$ пространства с $1 <$ $p$ $<\infty$ . Однако есть нормированные пространства, в которых это не так. Например, рассмотрим плоскость с нормой $ℓ$ $1$ ( манхэттенское расстояние ) и обозначим $x$ $= (1, 0)$ и $y$ $= (0, 1)$ . Тогда треугольник, образованный $x$ , $y$ и $x$ $+$ $y$ , невырожден, но ${\ Displaystyle \ | х + у \ | = \ | х \ | + \ | у \ |}$

{\ Displaystyle \ | х + у \ | = \ | (1,1) \ | = | 1 | + | 1 | = 2 = \ | х \ | + \ | у \ |.}

Примеры норм

Абсолютное значение как норма для реальной линии . Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютное значение удовлетворяло для любых действительных чисел $x$ и $y$ : ${\ Displaystyle | х + у | \ Leq | х | + | у |,}$ что он делает.

Доказательство:

{\ displaystyle - \ left \ vert x \ right \ vert \ leq x \ leq \ left \ vert x \ right \ vert}

{\ displaystyle - \ left \ vert y \ right \ vert \ leq y \ leq \ left \ vert y \ right \ vert}

После добавления

{\ Displaystyle - (\ влево \ верт х \ вправо \ верт + \ влево \ верт у \ вправо \ верт) \ Leq х + у \ Leq \ влево \ верт х \ вправо \ верт + \ влево \ верт у \ вправо \ vert}

Используйте тот факт, что (с заменой b на x + y и a на ), мы имеем ${\ displaystyle \ left \ vert b \ right \ vert \ leq a \ Leftrightarrow -a \ leq b \ leq a}$ ${\ Displaystyle \ влево \ верт х \ вправо \ верт + \ влево \ верт у \ вправо \ верт}$

{\ Displaystyle | х + у | \ Leq | х | + | у |}

Неравенство треугольника полезно в математическом анализе для определения наилучшей верхней оценки размера суммы двух чисел с точки зрения размеров отдельных чисел.

Существует также нижняя оценка, которую можно найти с помощью неравенства обратного треугольника, которое гласит, что для любых действительных чисел $x$ и $y$ :

{\ displaystyle | xy | \ geq {\ biggl |} | x | - | y | {\ biggr |}.}

Внутренний продукт как норма во внутреннем пространстве продукта . Если норма возникает из скалярного произведения (как в случае евклидовых пространств), то неравенство треугольника следует из неравенства Коши – Шварца следующим образом: даны векторы и , и обозначая скалярное произведение как : ${\ displaystyle x}$ ${\ displaystyle y}$ ${\ Displaystyle \ langle х, у \ rangle}$

${\ Displaystyle \ \| х + у \ \| ^ {2}}$	${\ displaystyle = \ langle x + y, x + y \ rangle}$
	${\ displaystyle = \ \| x \ \| ^ {2} + \ langle x, y \ rangle + \ langle y, x \ rangle + \ \| y \ \| ^ {2}}$
	${\ Displaystyle \ Leq \ \| х \ \| ^ {2} +2 \| \ langle x, y \ rangle \| + \ \| y \ \| ^ {2}}$
	${\ Displaystyle \ Leq \ \| х \ \| ^ {2} +2 \ \| х \ \| \ \| у \ \| + \ \| у \ \| ^ {2}}$ (по неравенству Коши – Шварца)
	${\ Displaystyle = \ влево (\ \| х \ \| + \ \| у \ \| \ вправо) ^ {2}}$ .

Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда $x$ и $y$ линейно зависимы. Неравенство превращается в равенство для линейно зависимых и тогда и только тогда, когда один из векторов $x$ или $y$ является неотрицательным скаляром другого. ${\ displaystyle \ langle x, y \ rangle + \ langle y, x \ rangle \ leq 2 \ left | \ left \ langle x, y \ right \ rangle \ right |}$ ${\ displaystyle x}$ ${\ displaystyle y}$

Извлечение квадратного корня из окончательного результата дает неравенство треугольника.

$p$ -норма: обычно используемой нормой являетсяp-норма: ${\ Displaystyle \ | х \ | _ {p} = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} \ right) ^ {1 / p} \,}$ где $x i$ - компоненты вектора $x$ . Для $р = 2$ $р$ -норма становится евклидовой нормой : ${\ displaystyle \ | x \ | _ {2} = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {2} \ right) ^ {1/2} = \ left (\ sum _ {i = 1} ^ {n} x_ {i} ^ {2} \ right) ^ {1/2} \,}$ что является теоремой Пифагора в $n$ -мерностях, очень частном случае, соответствующем норме внутреннего произведения. За исключением случая $p = 2$ , $p$ -норма не является нормой внутреннего произведения, потому что она не удовлетворяет закону параллелограмма . Неравенство треугольника для общих значений $p$ называется неравенством Минковского . Он принимает вид: ${\ displaystyle \ | x + y \ | _ {p} \ leq \ | x \ | _ {p} + \ | y \ | _ {p} \.}$

Метрическое пространство

В метрическом пространстве $M$ с метрикой $d$ неравенство треугольника является требованием для расстояния :

{\ Displaystyle d (х, \ z) \ Leq d (х, \ y) + d (у, \ z) \,}

для всех $х$ , $у$ , $г$ в $М$ . То есть расстояние от $x$ до $z$ не больше суммы расстояния от $x$ до $y$ и расстояния от $y$ до $z$ .

Неравенство треугольника отвечает за большую часть интересной структуры метрического пространства, а именно за сходимость. Это связано с тем, что остальные требования к метрике по сравнению с ними довольно упрощены. Например, тот факт, что любая сходящаяся последовательность в метрическом пространстве является последовательностью Коши, является прямым следствием неравенства треугольника, потому что если мы выберем любые $x n$ и $x m$ такие, что $d (x n, x) < ε / 2$ и $d (x m, x) < ε / 2$ , где $ε > 0$ задано и произвольно (как в определении предела в метрическом пространстве), то по неравенству треугольника $d (x n, x m) \leq d (x n, x) + d (x m, x) < ε / 2 + ε / 2 = ε$ , так что последовательность ${x n}$ по определению является последовательностью Коши.

Эта версия неравенства треугольника сводится к изложенной выше в случае нормированных векторных пространств, где метрика индуцируется через $d (x, y) ≔ ‖ x - y ‖$ , где $x - y$ является вектором, указывающим из точки $y$ в $x$ .

Обратное неравенство треугольника

Обратное неравенство треугольника является элементарным следствием неравенства треугольника , что дает нижнюю границу вместо верхних границ. Для плоской геометрии утверждение:

Любая сторона треугольника больше или равна разнице между двумя другими сторонами .

В случае нормированного векторного пространства утверждение таково:

{\ Displaystyle {\ bigg |} \ | х \ | - \ | у \ | {\ bigg |} \ leq \ | ху \ |,}

или для метрических пространств $| d (y, x) - d (x, z) | \leq d (y, z)$ . Это означает , что норма , а также функция расстояния являются липшицируемая с константой Липшица $1$ , и , следовательно, в частности , равномерно непрерывна . ${\ Displaystyle \ | \ cdot \ |}$ ${\ Displaystyle д (х, \ cdot)}$

Доказательство обратного треугольника использует неравенство правильного треугольника и : ${\ Displaystyle \ | Yx \ | = \ | {-} 1 (ху) \ | = | {-} 1 | \ cdot \ | ху \ | = \ | ху \ |}$

{\ Displaystyle \ | х \ | = \ | (ху) + у \ | \ leq \ | ху \ | + \ | у \ | \ Rightarrow \ | х \ | - \ | у \ | \ leq \ | ху \ |,}

{\ Displaystyle \ | у \ | = \ | (yx) + x \ | \ leq \ | yx \ | + \ | x \ | \ Rightarrow \ | x \ | - \ | y \ | \ geq - \ | xy \ |,}

Объединение этих двух утверждений дает:

{\ displaystyle - \ | xy \ | \ leq \ | x \ | - \ | y \ | \ leq \ | xy \ | \ Rightarrow {\ bigg |} \ | x \ | - \ | y \ | {\ bigg |} \ leq \ | xy \ |.}

Обращение в пространстве Минковского

Пространство Минковского метрика не является положительно определенной, что означает , что может иметь любой знак или исчезающие, даже если вектор х не равен нулю. Более того, если x и y - оба времениподобные векторы, лежащие в световом конусе будущего, неравенство треугольника отменяется: ${\ displaystyle \ eta _ {\ mu \ nu}}$ ${\ Displaystyle \ | х \ | ^ {2} = \ eta _ {\ mu \ nu} x ^ {\ mu} x ^ {\ nu}}$

{\ Displaystyle \ | х + у \ | \ geq \ | х \ | + \ | у \ |.}

Физическим примером этого неравенства является парадокс близнецов в специальной теории относительности . Такая же обратная форма неравенства выполняется, если оба вектора лежат в световом конусе прошлого, и если один или оба являются нулевыми векторами. Результат верен в n + 1 измерениях для любого n ≥ 1. Если плоскость, определяемая x и y , пространственноподобна (и, следовательно, является евклидовым подпространством), то выполняется обычное неравенство треугольника.

Смотрите также

Примечания

использованная литература

Педое, Дэниел (1988). Геометрия: всеобъемлющий курс . Дувр. ISBN 0-486-65812-0..
Рудин, Вальтер (1976). Принципы математического анализа . Нью-Йорк: Макгроу-Хилл . ISBN 0-07-054235-X..

внешние ссылки

Неравенство треугольников на ProofWiki

${\ Displaystyle \ \| х + у \ \| ^ {2}}$	${\ displaystyle = \ langle x + y, x + y \ rangle}$
	${\ displaystyle = \ \| x \ \| ^ {2} + \ langle x, y \ rangle + \ langle y, x \ rangle + \ \| y \ \| ^ {2}}$
	${\ Displaystyle \ Leq \ \| х \ \| ^ {2} +2 \| \ langle x, y \ rangle \| + \ \| y \ \| ^ {2}}$
	${\ Displaystyle \ Leq \ \| х \ \| ^ {2} +2 \ \| х \ \| \ \| у \ \| + \ \| у \ \| ^ {2}}$ (по неравенству Коши – Шварца)
	${\ Displaystyle = \ влево (\ \| х \ \| + \ \| у \ \| \ вправо) ^ {2}}$ .

Languages

In other projects