Тетрация - Tetration

В математике , тетрация (или гипер-4 ) является операция на основе итерированного или повторяются, возведение в степень . Это следующая гипероперация после возведения в степень , но до пентации . Слово было придумано Рубеном Луи Гудстайном от тетра- (четыре) и повторения .

Под определением повторного возведения в степень нотация Руди Ракера означает , что n копий a повторяются путем возведения в степень справа налево, т. Е. Применения времени возведения в степень . n называется «высотой» функции, а a называется «основанием», аналогично возведению в степень. Это будет читаться как « n- я тетрация а ». ${\ Displaystyle {^ {п} а}}$${\ Displaystyle {а ^ {а ^ {\ cdot ^ {\ cdot ^ {а}}}}}}$${\ displaystyle n-1}$

Тетрация также определяется рекурсивно как

${\ displaystyle {^ {n} a}: = {\ begin {cases} 1 & {\ text {if}} n = 0 \\ a ^ {\ left (^ {(n-1)} a \ right)} & {\ text {if}} n> 0 \ end {case}}}$,

разрешая попытки расширить тетрацию до не натуральных чисел, таких как действительные и комплексные числа.

Две инверсии тетрации называются суперкорнем и суперлогарифмом , аналогично корню n-й степени и логарифмическим функциям. Ни одна из трех функций не является элементарной .

Тетрация используется для записи очень больших чисел .

Вступление

Здесь показаны первые четыре гипероперации , при этом тетрация считается четвертой в серии. Унарная операция Последовательность , определяемая как , считается нулевой операцией. ${\ Displaystyle а '= а + 1}$

1. Добавление

   ${\ Displaystyle а + п = а + \ underbrace {1 + 1 + \ cdots +1} _ {п}}$

   n копий 1 добавлено к файлу .

2. Умножение

   ${\ Displaystyle а \ раз п = \ underbrace {а + а + \ cdots + а} _ {п}}$

   п копиисочетании добавлением.

3. Возведение в степень

   ${\ Displaystyle а ^ {п} = \ underbrace {а \ раз а \ раз \ cdots \ раз а} _ {п}}$

   n экземпляров a объединены путем умножения.

4. Тетрация

   ${\ displaystyle {^ {n} a} = \ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}} _ {n}}$

   п копиясочетании с экспоненциацией, вправо-налево.

Последовательность ( a ′ = a + 1) - самая простая операция; в то время как сложение ( a + n ) является основной операцией, для сложения натуральных чисел его можно рассматривать как последовательную последовательность n последователей a ; Умножение ( a  ×  n ) также является основной операцией, хотя для натуральных чисел его можно аналогичным образом рассматривать как связанное сложение, включающее n чисел от a . Возведение в степень можно представить как последовательное умножение, включающее n чисел a, и тетрацию ( ) как связанную степень, включающую n чисел a . Каждая из вышеперечисленных операций определяется повторением предыдущей; однако, в отличие от предшествующих операций, тетрация не является элементарной функцией . ${\ Displaystyle ^ {п} а \!}$

Параметр a называется базой , а параметр n - высотой . В исходном определении тетрации параметр высоты должен быть натуральным числом; например, было бы нелогично сказать, что «три подняли к себе отрицание пять раз» или «четыре подняли к себе половину времени». Однако так же, как сложение, умножение и возведение в степень могут быть определены способами, позволяющими расширять действительные и комплексные числа, было предпринято несколько попыток обобщить тетрацию на отрицательные числа, действительные числа и комплексные числа. Один из таких способов - использовать рекурсивное определение тетрации; для любого положительного действительного и неотрицательного целого числа мы можем определить рекурсивно как: ${\ displaystyle a> 0}$ ${\ Displaystyle п \ geq 0}$${\ Displaystyle \, \! {^ {п} а}}$

${\ displaystyle {^ {n} a}: = {\ begin {cases} 1 & {\ text {if}} n = 0 \\ a ^ {\ left (^ {(n-1)} a \ right)} & {\ text {if}} n> 0 \ end {case}}}$

Рекурсивное определение эквивалентно повторному возведению в степень для естественных высот; Однако, это определение допускает расширения для других высот , таких как , и так же - многие из этих расширений являются областями активных исследований. ${\ displaystyle ^ {0} а}$${\ displaystyle ^ {- 1} а}$${\ Displaystyle ^ {я} а}$

Терминология

Существует множество терминов для обозначения тетрации, каждый из которых имеет определенную логику, но некоторые из них не стали широко использоваться по той или иной причине. Вот сравнение каждого термина с его обоснованием и контробоснованием.

• Термин тетрация , введенный Гудстейном в его статье 1947 года « Трансфинитные порядки в рекурсивной теории чисел» (обобщение рекурсивного базового представления, используемого в теореме Гудстейна для использования более высоких операций), стал доминирующим. Это также было популяризировано в « Бесконечности и разуме» Руди Ракера .
• Термин сверхэкспоненциация был опубликован Бромером в его статье « Суперэкспоненцирование» в 1987 году. Ранее его использовал Эд Нельсон в своей книге «Предикативная арифметика», Princeton University Press, 1986.
• Термин гиперсила - это естественная комбинация гипер и мощи , которая точно описывает тетрацию. Проблема заключается в значении гипер по отношению к последовательности гиперопераций . При рассмотрении гиперопераций термин гипер относится ко всем рангам, а термин супер относится к рангу 4 или тетрации. Таким образом, с учетом этих соображений гиперсила вводит в заблуждение, поскольку имеет в виду только тетрацию.
• Термин « силовая башня» иногда используется в форме «силовая башня порядка n » для . Однако это неправильное название, потому что тетрация не может быть выражена с помощью повторяющихся степенных функций (см. Выше), поскольку это повторяющаяся экспоненциальная функция.${\ Displaystyle {\ \ на вершине {\}} {{\ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}}} \ на вершине n}}$

Частично из-за некоторой общей терминологии и подобной символики обозначений , тетрацию часто путают с тесно связанными функциями и выражениями. Вот несколько связанных терминов:

Термины, относящиеся к тетрации

Терминология	Форма
Тетрация	${\ Displaystyle а ^ {а ^ {\ cdot ^ {\ cdot ^ {а ^ {а}}}}}}$
Итерированные экспоненты	${\ Displaystyle а ^ {а ^ {\ cdot ^ {\ cdot ^ {а ^ {х}}}}}}$
Вложенные экспоненты (также башни)	${\ displaystyle a_ {1} ^ {a_ {2} ^ {\ cdot ^ {\ cdot ^ {a_ {n}}}}}}$
Бесконечные экспоненты (также башни)	${\ Displaystyle а_ {1} ^ {а_ {2} ^ {а_ {3} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

В первых двух выражениях a - это основание , а количество появлений a - это высота (добавьте единицу для x ). В третьем выражении n - высота , но каждое из оснований отличается.

Следует проявлять осторожность при обращении к повторяющимся экспонентам, так как выражения этой формы обычно называют повторным возведением в степень, что неоднозначно, поскольку это может означать либо повторные степени, либо повторные экспоненты .

Обозначение

Есть много разных стилей обозначений, которые можно использовать для выражения тетрации. Некоторые обозначения также могут использоваться для описания других гиперопераций , в то время как некоторые ограничиваются тетрацией и не имеют немедленного расширения.

Стили обозначений для тетрации

Имя	Форма	Описание
Обозначения Руди Ракера	${\ displaystyle \, {} ^ {n} а}$	Используется Маурером [1901] и Гудстейном [1947]; Книга Руди Ракера « Бесконечность и разум» популяризировала эти обозначения.
Обозначение Кнута со стрелкой вверх	${\ displaystyle a {\ uparrow \ uparrow} п}$	Позволяет расширить, добавив больше стрелок или, что еще более эффективно, указав стрелку.
Обозначение стрелок Конвея	${\ displaystyle a \ rightarrow п \ rightarrow 2}$	Позволяет расширять за счет увеличения числа 2 (эквивалент вышеуказанных расширений), но также, что еще более эффективно, за счет удлинения цепочки
Функция Аккермана	${\ displaystyle {} ^ {n} 2 = \ operatorname {A} (4, n-3) +3}$	Позволяет записать особый случай в терминах функции Аккермана. ${\ displaystyle a = 2}$
Итерированная экспоненциальная запись	${\ Displaystyle \ ехр _ {а} ^ {п} (1)}$	Позволяет простое расширение до повторяющихся экспонент от начальных значений, отличных от 1.
Обозначения Хушмана	${\ displaystyle {\ begin {align} & \ operatorname {uxp} _ {a} n \\ [2pt] & a ^ {\ frac {n} {}} \ end {align}}}$	Используется MH Hooshmand [2006].
Обозначения гиперопераций	${\ displaystyle {\ begin {align} & a [4] n \\ [2pt] & H_ {4} (a, n) \ end {align}}}$	Позволяет расширить за счет увеличения числа 4; это дает семейство гиперопераций .
Обозначение двойной вставки	a^^n	Поскольку стрелка вверх используется так же, как и каретка ( ^), тетрация может быть записана как ( ^^); удобно для ASCII .

В одной из приведенных выше обозначений используется итеративная экспоненциальная запись; в целом это определяется следующим образом:

${\ displaystyle \ exp _ {a} ^ {n} (x) = a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {x}}}}}}}$с н а с.

Для повторяющихся экспонент не так много обозначений, но вот несколько:

Стили обозначений для повторяющихся экспонент

Имя	Форма	Описание
Стандартные обозначения	${\ Displaystyle \ ехр _ {а} ^ {п} (х)}$	Эйлер ввел эту нотацию , и нотация итераций существует примерно столько же. ${\ Displaystyle \ ехр _ {а} (х) = а ^ {х}}$${\ Displaystyle е ^ {п} (х)}$
Обозначение Кнута со стрелкой вверх	${\ Displaystyle (а {\ вверх}) ^ {п} (х)}$	Позволяет использовать сверхмощные и суперэкспоненциальные функции за счет увеличения количества стрелок; используется в статье о больших числах .
Текстовое обозначение	exp_a^n(x)	Основано на стандартных обозначениях; удобно для ASCII .
Обозначение J	x^^:(n-1)x	Повторяет возведение в степень. См. J (язык программирования)

Примеры

Из-за чрезвычайно быстрого роста тетрации большинство значений в следующей таблице слишком велики для записи в научных обозначениях. В этих случаях используется итеративная экспоненциальная запись, чтобы выразить их в базе 10. Значения, содержащие десятичную точку, являются приблизительными.

Примеры тетрации

${\ displaystyle x}$	${\ displaystyle {} ^ {2} x}$	${\ displaystyle {} ^ {3} x}$	${\ displaystyle {} ^ {4} x}$	${\ displaystyle {} ^ {5} x}$
1	1	1	1	1
2	4	16	65 536	2 65 536 или (2,0035 × 10 19 728 )
3	27	7 625 597 484 987	${\ Displaystyle \ ехр _ {10} ^ {3} (1.09902)}$(3,6 × 10 12 цифр)	${\ Displaystyle \ ехр _ {10} ^ {4} (1.09902)}$
4	256	1,34078 × 10 154	${\ displaystyle \ exp _ {10} ^ {3} (2,18726)}$(8,1 × 10 153 цифр)	${\ displaystyle \ exp _ {10} ^ {4} (2,18726)}$
5	3,125	1,91 · 101 × 10 2184	${\ Displaystyle \ ехр _ {10} ^ {3} (3,33928)}$(1,3 × 10 2184 цифр)	${\ Displaystyle \ ехр _ {10} ^ {4} (3,33928)}$
6	46 656	2,65912 × 10 36,305	${\ Displaystyle \ ехр _ {10} ^ {3} (4,55997)}$(2,1 × 10 36 305 цифр)	${\ displaystyle \ exp _ {10} ^ {4} (4.55997)}$
7	823 543	3,75982 × 10 695 974	${\ displaystyle \ exp _ {10} ^ {3} (5,84259)}$(3,2 × 10 695 974 цифр)	${\ displaystyle \ exp _ {10} ^ {4} (5,84259)}$
8	16 777 216	6,01452 × 10 15,151,335	${\ displaystyle \ exp _ {10} ^ {3} (7.18045)}$(5,4 × 10 15,151,335 цифр)	${\ displaystyle \ exp _ {10} ^ {4} (7.18045)}$
9	387 420 489	4,28125 × 10 369 693 099	${\ displaystyle \ exp _ {10} ^ {3} (8,56784)}$(4,1 × 10 369 693 099 цифр)	${\ displaystyle \ exp _ {10} ^ {4} (8,56784)}$
10	10 000 000 000	10 10 000 000 000	${\ Displaystyle \ ехр _ {10} ^ {3} (10)}$(10 10 000 000 000 + 1 цифра)	${\ Displaystyle \ ехр _ {10} ^ {4} (10)}$

Характеристики

У тетрации есть несколько свойств, которые похожи на возведение в степень, а также свойства, которые являются специфическими для операции и теряются или приобретаются в результате возведения в степень. Поскольку возведение в степень не коммутируется , правила произведения и степени не имеют аналога с тетрацией; утверждения и не верны для большинства случаев. ${\ textstyle {} ^ {a} \ left ({} ^ {b} x \ right) = \ left ({} ^ {ab} x \ right)}$${\ textstyle {} ^ {a} \ left (xy \ right) = {} ^ {a} x {} ^ {a} y}$

Однако тетрация имеет другое свойство, в котором . Этот факт наиболее наглядно демонстрируется с помощью рекурсивного определения. Из этого свойства следует доказательство , которое позволяет переключать b и c в некоторых уравнениях. Доказательство выглядит следующим образом: ${\ textstyle {} ^ {a} x = x ^ {\ left ({} ^ {a-1} x \ right)}}$${\ displaystyle \ left ({} ^ {b} a \ right) ^ {\ left ({} ^ {c} a \ right)} = \ left ({} ^ {c + 1} a \ right) ^ { \ left ({} ^ {b-1} a \ right)}}$

${\ displaystyle {\ begin {align} & \ left ({} ^ {b} a \ right) ^ {\ left ({} ^ {c} a \ right)} \\ = {} & \ left (a ^ {{} ^ {b-1} a} \ right) ^ {\ left ({} ^ {c} a \ right)} \\ = {} & a ^ {\ left ({} ^ {b-1} a \ right) \ left ({} ^ {c} a \ right)} \\ = {} & a ^ {\ left ({} ^ {c} a \ right) \ left ({} ^ {b-1} a \ right)} \\ = {} & \ left ({} ^ {c + 1} a \ right) ^ {\ left ({} ^ {b-1} a \ right)} \ end {выровнено}}}$

Когда числа x и 10 взаимно просты , можно вычислить последние m десятичных цифр, используя теорему Эйлера , для любого целого числа m . ${\ Displaystyle \, \! \ ^ {а} х}$

Направление оценки

При оценке тетрации, выраженной как «башня возведения в степень», последовательное возведение в степень сначала выполняется на самом глубоком уровне (в обозначениях - на вершине). Например:

${\ Displaystyle \, \! \ ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 2 ^ {\ left (2 ^ {\ left (2 ^ {2} \ right)} \ right)} = 2 ^ {\ left (2 ^ {4} \ right)} = 2 ^ {16} = 65, \! 536}$

Этот порядок важен, потому что возведение в степень не ассоциативно , и оценка выражения в обратном порядке приведет к другому ответу:

${\ Displaystyle \, \! 2 ^ {2 ^ {2 ^ {2}}} \ neq \ left ({\ left (2 ^ {2} \ right)} ^ {2} \ right) ^ {2} = 4 ^ {2 \ cdot 2} = 256}$

Оценка выражения слева направо считается менее интересной; оценивая слева направо, любое выражение можно упростить . Из-за этого башни необходимо оценивать справа налево (или сверху вниз). Программисты называют этот выбор правоассоциативным . ${\ Displaystyle ^ {п} а \!}$${\ Displaystyle а ^ {\ влево (а ^ {п-1} \ вправо)} \! \!}$

Расширения

Тетрацию можно продлить двумя способами; в уравнении и основание a, и высота n могут быть обобщены с использованием определения и свойств тетрации. Хотя основание и высота могут быть расширены за пределы неотрицательных целых чисел в различные области , включая сложные функции, такие как и высоты бесконечного n , более ограниченные свойства тетрации снижают возможность расширения тетрации. ${\ Displaystyle ^ {п} а \!}$${\ displaystyle {^ {n} 0}}$${\ displaystyle {} ^ {n} я}$

Продление домена для баз

Базовый ноль

Показатель экспоненты не определен последовательно. Таким образом, тетрации четко не определяются формулой, приведенной ранее. Однако это хорошо определено и существует: ${\ displaystyle 0 ^ {0}}$${\ displaystyle \, {^ {n} 0}}$${\ displaystyle \ lim _ {x \ rightarrow 0} {} ^ {n} x}$

${\ displaystyle \ lim _ {x \ rightarrow 0} {} ^ {n} x = {\ begin {cases} 1, & n {\ text {even}} \\ 0, & n {\ text {odd}} \ end {случаи}}}$

Таким образом мы могли последовательно определять . Это аналогично определению . ${\ displaystyle {} ^ {n} 0 = \ lim _ {x \ rightarrow 0} {} ^ {n} x}$${\ displaystyle 0 ^ {0} = 1}$

При этом расширении, так что правило из исходного определения все еще сохраняется. ${\ displaystyle {} ^ {0} 0 = 1}$${\ displaystyle {^ {0} a} = 1}$

Комплексные базы

Поскольку комплексные числа могут быть возведены в степень , тетрация может применяться к основам вида z = a + bi (где a и b действительные). Например, в ⁿ z с z = i тетрация достигается за счет использования главной ветви натурального логарифма; используя формулу Эйлера, получаем соотношение:

${\ displaystyle i ^ {a + bi} = e ^ {{\ frac {1} {2}} {\ pi i} (a + bi)} = e ^ {- {\ frac {1} {2}} {\ pi b}} \ left (\ cos {\ frac {\ pi a} {2}} + i \ sin {\ frac {\ pi a} {2}} \ right)}$

Это предлагает рекурсивное определение для ^{n +1} i = a ′ + b′i для любого ⁿ i = a + bi :

${\ displaystyle {\ begin {align} a '& = e ^ {- {\ frac {1} {2}} {\ pi b}} \ cos {\ frac {\ pi a} {2}} \\ [ 2pt] b '& = e ^ {- {\ frac {1} {2}} {\ pi b}} \ sin {\ frac {\ pi a} {2}} \ end {выровнено}}}$

Можно получить следующие приблизительные значения:

Значения тетрации сложных оснований

${\ textstyle {} ^ {n} я}$	Приблизительное значение
${\ textstyle {} ^ {1} я = я}$	я
${\ textstyle {} ^ {2} я = я ^ {\ влево ({} ^ {1} я \ вправо)}}$	0,2079
${\ textstyle {} ^ {3} я = я ^ {\ влево ({} ^ {2} я \ вправо)}}$	0,9472 + 0,3208 я
${\ textstyle {} ^ {4} я = я ^ {\ влево ({} ^ {3} я \ вправо)}}$	0,0501 + 0,6021 я
${\ textstyle {} ^ {5} я = я ^ {\ влево ({} ^ {4} я \ вправо)}}$	0,3872 + 0,0305 я
${\ textstyle {} ^ {6} я = я ^ {\ влево ({} ^ {5} я \ вправо)}}$	0,7823 + 0,5446 я
${\ textstyle {} ^ {7} я = я ^ {\ влево ({} ^ {6} я \ вправо)}}$	0,1426 + 0,4005 я
${\ textstyle {} ^ {8} я = я ^ {\ влево ({} ^ {7} я \ вправо)}}$	0,5198 + 0,1184 я
${\ textstyle {} ^ {9} я = я ^ {\ влево ({} ^ {8} я \ вправо)}}$	0,5686 + 0,6051 я

Решение обратной зависимости, как и в предыдущем разделе, дает ожидаемые ⁰ i = 1 и ⁻¹ i = 0 , с отрицательными значениями n, дающими бесконечные результаты на мнимой оси. Построенная на комплексной плоскости , вся последовательность закручивается по спирали до предела 0,4383 + 0,3606 i , что можно интерпретировать как значение, где n бесконечно.

Такие последовательности тетраций изучаются со времен Эйлера, но плохо изучены из-за их хаотического поведения. Большинство опубликованных исследований исторически было сосредоточено на сходимости бесконечно повторяющейся экспоненциальной функции. Нынешним исследованиям в значительной степени способствовало появление мощных компьютеров с программным обеспечением для фрактальной и символьной математики. Многое из того, что известно о тетрации, получено из общих знаний о сложной динамике и конкретных исследований экспоненциальной карты.

Расширения домена на разную высоту

Бесконечные высоты

Тетрация может быть увеличена до бесконечных высот; т.е. для определенных значений a и n в существует хорошо определенный результат для бесконечного n . Это связано с тем, что для оснований в определенном интервале тетрация сходится к конечному значению, поскольку высота стремится к бесконечности . Например, сходится к 2, и поэтому можно сказать, что он равен 2. Тенденцию к 2 можно увидеть, оценив небольшую конечную башню: ${\ displaystyle {} ^ {n} а}$${\ displaystyle {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

${\ displaystyle {\ begin {align} {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}) }} ^ {1.414}}}}} & \ приблизительно {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {1.63 }}}} \\ & \ приблизительно {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {1.76}}} \\ & \ приблизительно {\ sqrt {2 }} ^ {{\ sqrt {2}} ^ {1.84}} \\ & \ приблизительно {\ sqrt {2}} ^ {1.89} \\ & \ приблизительно 1,93 \ end {выровнено}}}$

В общем, бесконечно повторяемая экспонента , определяемая как предел, когда n стремится к бесконечности, сходится при e ^{- e} ≤ x ≤ e ^{1 / e} , примерно в интервале от 0,066 до 1,44, результат, показанный Леонардом Эйлером . Предел, если он существует, является положительным действительным решением уравнения y = x ^y . Таким образом, x = y ^{1 / y} . Предел, определяющий бесконечную экспоненту x , не существует, когда x > e ^{1 / e,} потому что максимум y ^{1 / y} равен e ^{1 / e} . Предел также не существует, когда 0 < x < e ^{- e} . ${\ Displaystyle х ^ {х ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} \! \!}$${\ Displaystyle {} ^ {п} х}$

Это может быть расширено до комплексных чисел z с определением:

${\ Displaystyle {} ^ {\ infty} z = z ^ {z ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} = {\ frac {\ mathrm {W} (- \ ln {z}) } {- \ ln {z}}} ~,}$

где W представляет W-функцию Ламберта .

Поскольку предел y = ^∞ x (если он существует на положительной вещественной прямой, т. Е. Для e ^{- e} ≤ x ≤ e ^{1 / e} ) должен удовлетворять x ^y = y, мы видим, что x ↦ y = ^∞ x is (нижняя ветвь ) функция, обратная y ↦ x = y ^{1 / y} .

Отрицательные высоты

Мы можем использовать рекурсивное правило для тетрации,

${\ displaystyle {^ {k + 1} a} = a ^ {\ left ({^ {k} a} \ right)},}$

доказать : ${\ displaystyle {} ^ {- 1} а}$

${\ displaystyle ^ {k} a = \ log _ {a} \ left (^ {k + 1} a \ right);}$

Подстановка −1 вместо k дает

${\ displaystyle {} ^ {- 1} a = \ log _ {a} \ left ({} ^ {0} a \ right) = \ log _ {a} 1 = 0}$.

Таким образом нельзя точно определить меньшие отрицательные значения. Подставляя −2 вместо k в том же уравнении, получаем

${\ displaystyle {} ^ {- 2} a = \ log _ {a} \ left ({} ^ {- 1} a \ right) = \ log _ {a} 0 = - \ infty}$

который не совсем точно определен. Однако иногда их можно рассматривать как наборы.

В самом деле , любое определение согласуется с правилом, потому что ${\ displaystyle n = 1}$${\ Displaystyle \, \! {^ {- 1} 1}}$

${\ displaystyle {^ {0} 1} = 1 = 1 ^ {n}}$для любого .${\ Displaystyle \, \! п = {^ {- 1} 1}}$

Реальные высоты

В настоящее время не существует общепринятого решения общей проблемы расширения тетрации до действительных или комплексных значений n . Однако к этому вопросу применялось несколько подходов, и различные подходы изложены ниже.

В общем, проблема заключается в нахождении - для любого действительного a > 0 - суперэкспоненциальной функции над действительным x > −2, которая удовлетворяет ${\ Displaystyle \, е (х) = {} ^ {х} а}$

• ${\ displaystyle \, {} ^ {- 1} а = 0}$
• ${\ Displaystyle \, {} ^ {0} а = 1}$
• ${\ displaystyle \, {} ^ {x} a = a ^ {\ left ({} ^ {x-1} a \ right)}}$для всех настоящих ${\ displaystyle x> -1.}$

Чтобы найти более естественное расширение, обычно требуется одно или несколько дополнительных требований. Обычно это некоторая совокупность следующего:

• Непрерывности требование ( как правило , только , что является непрерывным в обоих переменных ).${\ displaystyle {} ^ {x} а}$${\ displaystyle x> 0}$
• Дифференцируемоести требование (может быть один, два, K раз, или бесконечно дифференцируемых в х ).
• Регулярность требование (подразумевая дважды дифференцируемых в х ) , что:

${\ displaystyle \ left ({\ frac {d ^ {2}} {dx ^ {2}}} f (x)> 0 \ right)}$ для всех ${\ displaystyle x> 0}$

Четвертое требование различается от автора к автору и от подходов. Есть два основных подхода к расширению тетрации до реальных высот; один основан на требовании регулярности , а другой основан на требовании дифференцируемости . Эти два подхода кажутся настолько разными, что их нельзя согласовать, поскольку они дают результаты, несовместимые друг с другом.

Когда определено для интервала длины один, вся функция легко следует для всех x > −2 . ${\ displaystyle \, {} ^ {x} а}$

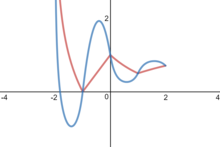
Линейное приближение для реальных высот

Линейное приближение (решение к требованию непрерывности, приближение к требованию дифференцируемости) определяется по формуле:

${\ displaystyle {} ^ {x} a \ приблизительно {\ begin {cases} \ log _ {a} \ left (^ {x + 1} a \ right) & x \ leq -1 \\ 1 + x & -1 < x \ leq 0 \\ a ^ {\ left (^ {x-1} a \ right)} & 0 <x \ end {case}}}$

следовательно:

Значения линейной аппроксимации

Приближение	Домен
${\ textstyle {} ^ {x} а \ приблизительно x + 1}$	для −1 < x <0
${\ textstyle {} ^ {x} а \ приблизительно а ^ {х}}$	для 0 < x <1
${\ textstyle {} ^ {x} а \ приблизительно а ^ {а ^ {(х-1)}}}$	для 1 < x <2

и так далее. Однако он дифференцируем только кусочно; при целых значениях x производная умножается на . Он непрерывно дифференцируем тогда и только тогда, когда . Например, используя эти методы и${\ Displaystyle \ ln {а}}$${\ displaystyle x> -2}$${\ displaystyle a = e}$${\ displaystyle {} ^ {\ frac {\ pi} {2}} е \ приблизительно 5,868 ...}$${\ displaystyle {} ^ {- 4.3} 0,5 \ приблизительно 4,03335 ...}$

Основная теорема в статье Хушманда гласит: Пусть . Если является непрерывным и удовлетворяет условиям: ${\ Displaystyle 0 <а \ neq 1}$${\ displaystyle f: (- 2, + \ infty) \ rightarrow \ mathbb {R}}$

• ${\ Displaystyle е (х) = а ^ {е (х-1)} \; \; {\ текст {для всех}} \; \; х> -1, \; f (0) = 1,}$
• ${\ displaystyle f}$дифференцируема на (−1, 0) ,
• ${\ displaystyle f ^ {\ prime}}$- неубывающая или невозрастающая функция на (−1, 0) ,
• ${\ displaystyle f ^ {\ prime} \ left (0 ^ {+} \ right) = (\ ln a) f ^ {\ prime} \ left (0 ^ {-} \ right) {\ text {или}} f ^ {\ prime} \ left (-1 ^ {+} \ right) = f ^ {\ prime} \ left (0 ^ {-} \ right).}$

то однозначно определяется уравнением ${\ displaystyle f}$

${\ displaystyle f (x) = \ exp _ {a} ^ {[x]} \ left (a ^ {(x)} \ right) = \ exp _ {a} ^ {[x + 1]} (( x)) \ quad {\ text {для всех}} \; \; x> -2,}$

где обозначает дробную часть х , а это - итерированная функция функции . ${\ Displaystyle (х) = х- [х]}$${\ Displaystyle \ ехр _ {а} ^ {[х]}}$${\ Displaystyle [х]}$${\ Displaystyle \ ехр _ {а}}$

Доказательство состоит в том, что из условий со второго по четвертое тривиально следует, что f - линейная функция на [−1, 0] .

Линейная аппроксимация естественной функции тетрации непрерывно дифференцируема, но ее вторая производная не существует при целых значениях ее аргумента. Хушманд вывел для него другую теорему единственности, которая гласит: ${\ displaystyle {} ^ {x} e}$

Если - непрерывная функция, удовлетворяющая: ${\ displaystyle f: (- 2, + \ infty) \ rightarrow \ mathbb {R}}$

• ${\ Displaystyle е (х) = е ^ {е (х-1)} \; \; {\ текст {для всех}} \; \; х> -1, \; f (0) = 1,}$
• ${\ displaystyle f}$выпукла на (−1, 0) ,
• ${\ displaystyle f ^ {\ prime} \ left (0 ^ {-} \ right) \ leq f ^ {\ prime} \ left (0 ^ {+} \ right).}$

тогда . [Вот имя Хушманда для линейного приближения к естественной функции тетрации.] ${\ displaystyle f = {\ text {uxp}}}$${\ displaystyle f = {\ text {uxp}}}$

Доказательство почти такое же, как и раньше; рекурсивное уравнение гарантирует, что, а затем из условия выпуклости следует, что это линейно на (−1, 0) . ${\ displaystyle f ^ {\ prime} (- 1 ^ {+}) = f ^ {\ prime} (0 ^ {+}),}$${\ displaystyle f}$

Таким образом, линейное приближение к естественной тетрации является единственным решением уравнения и который является выпуклым на (-1, + ∞) . Все остальные достаточно дифференцируемые решения должны иметь точку перегиба на интервале (−1, 0) . ${\ Displaystyle е (х) = е ^ {е (х-1)} \; \; (х> -1)}$${\ displaystyle f (0) = 1}$

Аппроксимации высших порядков для реальных высот

Помимо линейных приближений, квадратичное приближение (к требованию дифференцируемости) определяется следующим образом:

${\ displaystyle {} ^ {x} a \ приблизительно {\ begin {cases} \ log _ {a} \ left ({} ^ {x + 1} a \ right) & x \ leq -1 \\ 1 + {\ frac {2 \ ln (a)} {1 \; + \; \ ln (a)}} x - {\ frac {1 \; - \; \ ln (a)} {1 \; + \; \ ln (a)}} x ^ {2} & - 1 <x \ leq 0 \\ a ^ {\ left ({} ^ {x-1} a \ right)} & x> 0 \ end {case}}}$

которая дифференцируема для всех , но не дифференцируема дважды. Например, если это то же самое, что и линейное приближение. ${\ displaystyle x> 0}$${\ displaystyle {} ^ {\ frac {1} {2}} 2 \ приблизительно 1.45933 ...}$${\ displaystyle a = e}$

Из-за способа вычисления эта функция не «сокращается», в отличие от экспонент, где . А именно, ${\ displaystyle \ left (a ^ {\ frac {1} {n}} \ right) ^ {n} = a}$

${\ displaystyle {} ^ {n} \ left ({} ^ {\ frac {1} {n}} a \ right) = \ underbrace {\ left ({} ^ {\ frac {1} {n}} a \ right) ^ {\ left ({} ^ {\ frac {1} {n}} a \ right) ^ {\ cdot ^ {\ cdot ^ {\ cdot ^ {\ cdot ^ {\ left ({} ^ { \ frac {1} {n}} a \ right)}}}}}}} _ {n} \ neq a}$.

Так же, как существует квадратичное приближение, существуют также кубические приближения и методы обобщения на приближения степени n , хотя они гораздо более громоздкие.

Сложные высоты

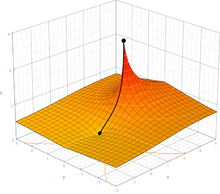
Теперь доказано, что существует единственная функция F, которая является решением уравнения F ( z + 1) = exp ( F ( z )) и удовлетворяет дополнительным условиям, что F (0) = 1 и F ( z ) приближается к неподвижным точкам логарифма (примерно 0,318 ± 1,337 я ) в г приближается ± я ∞ и F является голоморфным во всей комплексном г - плоскости, за исключением той части вещественной оси при г ≤ -2 . Это доказательство подтверждает предыдущую гипотезу . Построение такой функции было первоначально продемонстрировано Кнезером в 1950 году. Комплексное отображение этой функции показано на рисунке справа. Доказательство также работает для других оснований, кроме e , если основание больше, чем . Последующие работы распространили строительство на все сложные базы. Комплексное приближение этой функции с двойной точностью доступно в Интернете. ${\ displaystyle e ^ {\ frac {1} {e}} \ приблизительно 1,445}$

Требование голоморфности тетрации важно для ее уникальности. Многие функции S могут быть построены как

${\ Displaystyle S (z) = F \! \ left (~ z ~ + \ sum _ {n = 1} ^ {\ infty} \ sin (2 \ pi nz) ~ \ alpha _ {n} + \ sum _ {n = 1} ^ {\ infty} {\ Big (} 1- \ cos (2 \ pi nz) {\ Big)} ~ \ beta _ {n} \ right)}$

где α и β - действительные последовательности, которые убывают достаточно быстро, чтобы обеспечить сходимость ряда , по крайней мере, при умеренных значениях Im  z .

Функция S удовлетворяет уравнениям тетрации S ( z + 1) = exp ( S ( z )) , S (0) = 1 , и если α _n и β _{n стремятся} к 0 достаточно быстро, она будет аналитической в ​​окрестности положительного реальная ось. Однако, если некоторые элементы { α } или { β } не равны нулю, то функция S имеет множество дополнительных сингулярностей и разрезов в комплексной плоскости из-за экспоненциального роста sin и cos вдоль мнимой оси; чем меньше коэффициенты { α } и { β } , тем дальше эти особенности находятся от действительной оси.

Распространение тетрации на комплексную плоскость, таким образом, существенно для уникальности; вещественно-аналитическая тетрация не является уникальной.

Неэлементарная рекурсивность

Тетрация (ограниченная ) не является элементарной рекурсивной функцией . По индукции можно доказать, что для каждой элементарной рекурсивной функции f существует константа c такая, что ${\ Displaystyle \ mathbb {N} ^ {2}}$

${\ displaystyle f (x) \ leq \ underbrace {2 ^ {2 ^ {\ cdot ^ {\ cdot ^ {x}}}}} _ {c}.}$

Обозначим правую часть через . Предположим противное, что тетрация элементарно рекурсивна. также элементарно рекурсивно. По полученному неравенству существует постоянная c такая, что . Допуская , мы получаем противоречие. ${\ Displaystyle г (с, х)}$${\ Displaystyle г (х, х) +1}$${\ Displaystyle г (х, х) +1 \ Leq г (с, х)}$${\ displaystyle x = c}$${\ Displaystyle г (с, с) +1 \ leq г (с, с)}$

Обратные операции

Возведение в степень имеет две обратные операции; корни и логарифмы . Аналогичным образом, обратная сторона тетрации часто называется суперкорнем и суперлогарифмом (на самом деле, все гипероперации, большие или равные 3, имеют аналогичные обратные); например, в функции две инверсии - это кубический суперкорень y и основание суперлогарифма  y числа x . ${\ Displaystyle {^ {3}} у = х}$

Супер-корень

Суперкорень - это операция, обратная тетратированию по отношению к основанию: если , то y является n- м суперкорнем x ( или ). ${\ Displaystyle ^ {п} у = х}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {4}}$

Например,

${\ displaystyle ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 65 {,} 536}$

так что 2 - это 4-й суперкорень из 65 536.

Квадратный суперкорень

Второй порядок супер-корень , квадрат супер-корень , или супер квадратный корень имеет два эквивалентных обозначение, и . Это инверсия и может быть представлена функцией Ламберта W : ${\ Displaystyle \ mathrm {ssrt} (х)}$${\ displaystyle {\ sqrt {x}} _ {s}}$${\ Displaystyle ^ {2} х = х ^ {х}}$

${\ Displaystyle \ mathrm {ssrt} (х) = е ^ {W (\ ln x)} = {\ frac {\ ln x} {W (\ ln x)}}}$

Функция также иллюстрирует отражающую природу функций корня и логарифма, поскольку приведенное ниже уравнение справедливо только в том случае, если : ${\ Displaystyle у = \ mathrm {ssrt} (х)}$

${\ displaystyle {\ sqrt [{y}] {x}} = \ log _ {y} x}$

Как и квадратные корни , квадратный суперкорень x может не иметь единственного решения. В отличие от квадратных корней, определение количества квадратных суперкорней x может быть трудным. В общем, если , то x имеет два положительных квадратных суперкорня между 0 и 1; и если , то x имеет один положительный квадратный суперкорень больше 1. Если x положителен и меньше, он не имеет никаких вещественных квадратных суперкорней, но приведенная выше формула дает счетное бесконечное количество комплексных корней для любого конечного x не равно 1. Функция использовалась для определения размера кластеров данных . ${\ Displaystyle е ^ {- 1 / е} <х <1}$${\ displaystyle x> 1}$${\ displaystyle e ^ {- 1 / e}}$

В : ${\ displaystyle x = 1}$

${\ displaystyle \ mathrm {ssqrt} (x) = 1 + (x-1) - (x-1) ^ {2} + {\ frac {3} {2}} (x-1) ^ {3} - {\ frac {17} {6}} (x-1) ^ {4} + {\ frac {37} {6}} (x-1) ^ {5} - {\ frac {1759} {120}} (x-1) ^ {6} + {\ frac {13279} {360}} (x-1) ^ {7} + \ mathrm {O} \ left ((x-1) ^ {8} \ right) }$

Другие супер-корни

Для каждого целого числа п > 2 , функция ^п х определена и возрастает при х ≥ 1 , а ^п 1 = 1 , так что п - й супер-корень х , , существует при х ≥ 1 . ${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Одной из более простых и быстрых формул суперкорня третьей степени является рекурсивная формула, если: «x ^ x ^ x = a», а затем x (n + 1) = exp (W (W (x (n ) * ln (a)))), например x (0) = 1.

Однако, если используется приведенное выше линейное приближение , то если −1 < y ≤ 0 , значит, существовать не может. ${\ Displaystyle ^ {у} х = у + 1}$${\ displaystyle ^ {y} {\ sqrt {y + 1}} _ {s}}$

Точно так же, как квадратный суперкорень, терминология для других суперкорней может быть основана на нормальных корнях : «кубические суперкорни» могут быть выражены как ; «4-й суперкорень» можно выразить как ; а " n- й супер-корень" есть . Обратите внимание, что это может быть не однозначно определено, потому что может быть более одного корня n- ^{й степени} . Так , например, х имеют единственный (реальный) супер-корень , если п является нечетным , и до двух , если п является даже . ${\ displaystyle {\ sqrt [{3}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{4}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Как и в случае с расширением тетрации до бесконечных высот, суперкорень может быть расширен до n = ∞ , будучи хорошо определенным, если 1 / e ≤ x ≤ e . Обратите внимание на это и, следовательно, на то . Следовательно, когда она четко определена и, в отличие от обычной тетрации, является элементарной функцией . Например, . ${\ displaystyle x = {^ {\ infty} y} = y ^ {\ left [^ {\ infty} y \ right]} = y ^ {x},}$${\ Displaystyle у = х ^ {1 / х}}$${\ displaystyle {\ sqrt [{\ infty}] {x}} _ {s} = x ^ {1 / x}}$${\ displaystyle {\ sqrt [{\ infty}] {2}} _ {s} = 2 ^ {1/2} = {\ sqrt {2}}}$

Из теоремы Гельфонда – Шнайдера следует, что суперкорень для любого натурального n либо целочислен, либо трансцендентен , и может быть целым или иррациональным. Остается открытым вопрос, являются ли иррациональные суперкорни трансцендентными в последнем случае. ${\ displaystyle {\ sqrt {n}} _ {s}}$${\ displaystyle {\ sqrt [{3}] {n}} _ {s}}$

Суперлогарифм

После выбора непрерывно возрастающего (по x ) определения тетрации ^x a соответствующий суперлогарифм or определяется для всех действительных чисел x и a > 1 . ${\ displaystyle \ operatorname {slog} _ {a} x}$${\ Displaystyle \ журнал _ {а} ^ {4} х}$

Функция slog _a  x удовлетворяет:

${\ displaystyle {\ begin {array} {lcl} \ operatorname {slog} _ {a} {^ {x} a} & = & x \\\ operatorname {slog} _ {a} a ^ {x} & = & 1+ \ operatorname {slog} _ {a} x \\\ operatorname {slog} _ {a} x & = & 1+ \ operatorname {slog} _ {a} \ log _ {a} x \\\ operatorname {slog} _ {a } x &> & - 2 \ end {массив}}}$

Открытые вопросы

Помимо проблем с расширениями тетрации, есть несколько открытых вопросов, касающихся тетрации, особенно когда это касается отношений между системами счисления, такими как целые числа и иррациональные числа :

• Неизвестно, существует ли натуральное число n, для которого ⁿ π или ⁿ e является целым числом. В частности, неизвестно, является ли ⁴ π или ⁵ e целым числом.
• Неизвестно, является ли ⁿ q целым числом для любого положительного целого числа n и положительного нецелого рационального q . Например, неизвестно, является ли положительный корень уравнения ⁴ x = 2 рациональным числом.

Смотрите также

• Функция Аккермана
• Обозначение Big O
• Двойная экспоненциальная функция
• Гипероперация
• Итерированный логарифм
• Симметричная арифметика индекса уровня

Примечания

использованная литература

• Даниэль Гейслер, Tetration
• Иоаннис Галидакис, О расширении hyper4 на нецелые числа (без даты, 2006 г. или ранее) (более простой и удобный для чтения обзор следующей ссылки)
• Иоаннис Галидакис, О расширении Hyper4 и нотации стрелки вверх Кнута на вещественные числа (без даты, 2006 г. или ранее).
• Роберт Мунафо, Расширение функции hyper4 на вещественные числа (неформальное обсуждение расширения тетрации на действительные числа.)
• Лоде Вандевенне, Тетрация квадратного корня из двух . (2004). (Попытка расширить тетрацию до действительных чисел.)
• Иоаннис Галидакис, математика , (Окончательный список ссылок на исследования тетрации. Много информации о W-функции Ламберта, римановых поверхностях и аналитическом продолжении.)
• Джозеф МакДонелл, Некоторые критические точки функции гипермощности .
• Дэйв Л. Ренфро, веб-страницы для бесконечно повторяющихся экспонент
• Кнобель, Р. (1981). «Экспоненты повторяются». Американский математический ежемесячник . 88 (4): 235–252. DOI : 10.1080 / 00029890.1981.11995239 .
• Ханс Маурер, "Убер Die Funktion für ganzzahliges Argument (Abundanzen)". Mittheilungen der Mathematische Gesellschaft в Гамбурге 4 , (1901), стр. 33–50. (Ссылка на использование из статьи Кнобеля.)${\ Displaystyle у = х ^ {[х ^ {[х (\ cdots)]}]}}$ ${\ Displaystyle \ {^ {п} а}}$
• Четвертая операция
• Лука Морони, Странные свойства башни бесконечной силы ( https://arxiv.org/abs/1908.05559 )

дальнейшее чтение

• Галидакис, Иоаннис; Вайсштейн, Эрик Вольфганг . «Энергетическая башня» . MathWorld . Проверено 5 июля 2019 .