Формула шнурков - Shoelace formula

Формула Шнурок или алгоритм Шнурок (также известный как формула области Гаусса и в формуле сюрвейера ) представляет собой математический алгоритм для определения площади в виде простого многоугольника , вершины которого описываются их декартовы координаты в плоскости. Пользователь перемножает соответствующие координаты, чтобы найти область, охватывающую многоугольник , и вычитает ее из окружающего многоугольника, чтобы найти область внутри многоугольника. Это называется формулой шнурка из-за постоянного перемножения координат, составляющих многоугольник, как при продевании шнурков. Его также иногда называют методом шнурков . Он применяется, в частности, в геодезии и лесном хозяйстве.

Формула была описана Альбрехтом Людвигом Фридрихом Мейстером (1724–1788) в 1769 году и Карлом Фридрихом Гауссом в 1795 году. Ее можно проверить, разделив многоугольник на треугольники , и ее можно рассматривать как частный случай теоремы Грина .

Формула площади получается путем взятия каждого ребра AB и вычисления площади треугольника ABO с вершиной в исходной точке O путем взятия перекрестного произведения (которое дает площадь параллелограмма ) и деления на 2. Когда каждый оборачивается вокруг Для многоугольника эти треугольники с положительной и отрицательной областями будут перекрываться, а области между исходной точкой и многоугольником будут исключены и суммированы до 0, в то время как останется только область внутри ссылочного треугольника. Вот почему формула называется формулой геодезиста, поскольку «геодезист» стоит в начале координат; при движении против часовой стрелки положительная область добавляется при движении слева направо и отрицательная область добавляется при движении справа налево с точки зрения исходной точки.

Формула площади также может быть применена к самоперекрывающимся полигонам, поскольку значение площади по-прежнему ясно, даже если самоперекрывающиеся полигоны обычно не просты . Более того, самоперекрывающийся многоугольник может иметь несколько «интерпретаций», но формула Shoelace может использоваться, чтобы показать, что площадь многоугольника одинакова независимо от интерпретации.

Заявление

Формулу можно представить выражением

${\ displaystyle {\ begin {align} \ mathbf {A} & = {1 \ over 2} \ left | \ left (\ sum _ {i = 1} ^ {n-1} x_ {i} y_ {i + 1} \ right) + x_ {n} y_ {1} - \ left (\ sum _ {i = 1} ^ {n-1} x_ {i + 1} y_ {i} \ right) -x_ {1} y_ {n} \ right | \\ [4pt] & = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + \ cdots + x_ {n-1} y_ { n} + x_ {n} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} - \ cdots -x_ {n} y_ {n-1} -x_ {1} y_ { п} | \ конец {выровнено}}}$

куда

• A - площадь многоугольника,
• n - количество сторон многоугольника, а
• ( x _i ,  y _i ), i  = 1, 2, ...,  n - упорядоченные вершины (или «углы») многоугольника.

Альтернативно

${\ displaystyle {\ begin {align} \ mathbf {A} & = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} x_ {i} (y_ {i + 1} -y_ {i-1}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} y_ {i} (x_ {i + 1} -x_ {i-1}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}) \ right | \\ [5pt] & = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} (x_ {i + 1} + x_ {i}) (y_ {i + 1} - y_ {i}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} \ det {\ begin {pmatrix} x_ {i} & x_ {i + 1} \\ y_ {i} & y_ {i + 1} \ end {pmatrix}} \ right | \ end {выровнено}}}$

где x _{n +1} = x ₁ и x ₀ = x _n , а также y _{n +1} = y ₁ и y ₀ = y _n .

Если точки помечены последовательно против часовой стрелки, то сумма вышеуказанных определителей положительна и знаки абсолютного значения могут быть опущены; если они помечены по часовой стрелке, сумма определителей будет отрицательной. Это потому, что формулу можно рассматривать как частный случай теоремы Грина .

Особенно краткое изложение формулы можно дать в терминах внешней алгебры . Если - последовательные вершины многоугольника (рассматриваемые как векторы в декартовой плоскости), то ${\ displaystyle v_ {1}, \ dots, v_ {n}}$

${\ displaystyle A = {\ frac {1} {2}} \ cdot \ left | \ sum _ {i = 1} ^ {n} v_ {i} \ wedge v_ {i + 1} \ right |.}$

Доказательства

Доказательство треугольника

Ссылаясь на рисунок, позвольте быть площадью треугольника, вершины которого задаются координатами, и нарисуйте прямоугольник минимальной площади вокруг треугольника так, чтобы его стороны были параллельны осям или . По крайней мере, одна вершина треугольника будет в углу прямоугольника. На рисунке площади трех окружающих треугольников равны и, очевидно , равны площади прямоугольника (назовем его ) за вычетом площадей трех других треугольников: ${\ displaystyle \ mathbf {A}}$${\ displaystyle (x_ {1}, y_ {1}), (x_ {2}, y_ {2}),}$${\ displaystyle (x_ {3}, y_ {3}).}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle \ mathbf {C}, \ mathbf {D},}$${\ displaystyle \ mathbf {E}.}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {R}}$

${\ Displaystyle \ mathbf {A} = \ mathbf {R} - \ mathbf {C} - \ mathbf {D} - \ mathbf {E}}$

При осмотре рисунка видно, что площади даны как

${\ displaystyle \ mathbf {R} = (x_ {3} -x_ {2}) (y_ {1} -y_ {3}) = (x_ {3} y_ {1} + x_ {2} y_ {3} ) - (x_ {3} y_ {3} + x_ {2} y_ {1})}$

${\ displaystyle - \ mathbf {C} = - {\ frac {1} {2}} (x_ {3} -x_ {2}) (y_ {2} -y_ {3}) = {\ frac {1} {2}} (- x_ {3} y_ {2} -x_ {2} y_ {3}) + {\ frac {1} {2}} (x_ {3} y_ {3} + x_ {2} y_ {2})}$

${\ displaystyle - \ mathbf {D} = - {\ frac {1} {2}} (x_ {3} -x_ {1}) (y_ {1} -y_ {3}) = {\ frac {1} {2}} (- x_ {3} y_ {1} -x_ {1} y_ {3}) + {\ frac {1} {2}} (x_ {3} y_ {3} + x_ {1} y_ {1})}$

${\ displaystyle - \ mathbf {E} = - {\ frac {1} {2}} (x_ {1} -x_ {2}) (y_ {1} -y_ {2}) = {\ frac {1} {2}} (- x_ {1} y_ {1} -x_ {2} y_ {2}) + {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {1})}$

Сбор сроков и перестановка урожаев

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} ((x_ {2} y_ {3} -x_ {3} y_ {2}) - (x_ {1} y_ {3} - x_ {3} y_ {1}) + (x_ {1} y_ {2} -x_ {2} y_ {1}))}$

который можно записать как определитель

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} {\ begin {vmatrix} 1 & 1 & 1 \\ x_ {1} & x_ {2} & x_ {3} \\ y_ {1} & y_ {2} & y_ {3} \ end {vmatrix}}}$

Если координаты записывать по часовой стрелке, значение определителя будет ${\ displaystyle - \ mathbf {A}.}$

Переставляем по-другому

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2 } г_ {1} -x_ {3} г_ {2} -x_ {1} г_ {3} |}$

которая является формой формулы шнурка. Эту формулу можно расширить, чтобы найти площадь любого многоугольника, поскольку простой многоугольник можно разделить на треугольники.

Доказательство для четырехугольника и общего многоугольника

Нахождение площади четырехугольника демонстрирует, как формула шнурков обобщается на любой многоугольник путем деления многоугольника на треугольники. Рассмотрим фигуру четырехугольника, координаты которого отмечены в порядке против часовой стрелки. Четырехугольник разделен на два треугольника с площадями и Используя формулу треугольника для каждого треугольника, мы получаем ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {B}.}$

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2 } г_ {1} -x_ {3} г_ {2} -x_ {1} г_ {3})}$

${\ displaystyle \ mathbf {B} = {\ frac {1} {2}} (x_ {1} y_ {3} + x_ {3} y_ {4} + x_ {4} y_ {1} -x_ {3 } г_ {1} -x_ {4} г_ {3} -x_ {1} г_ {4})}$

Поскольку оба треугольника были начерчены против часовой стрелки, обе области положительны, и мы получаем площадь четырехугольника, складывая две области. Последний положительный член и последний отрицательный член отмены с первым положительным членом и первым отрицательным сроком предоставления ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {B}}$

${\ displaystyle \ mathbf {A} _ {\ text {quad.}} = {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3 } y_ {4} + x_ {4} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {1} y_ {4} ).}$

Примеры

Пользователь должен знать точки многоугольника на декартовой плоскости. Например, возьмем треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмите первую координату x и умножьте ее на второе значение y , затем возьмите вторую координату x, умножьте ее на третье значение y и повторите столько раз, пока это не будет сделано для всех требуемых точек. Это можно представить следующей формулой:

${\ displaystyle \ mathbf {A} _ {\ text {tri.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1 } -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {1} y_ {3} |}$

для x _i и y _i, представляющих каждую соответствующую координату. Эта формула является просто расширением приведенных выше для случая n = 3. Используя ее, можно найти, что площадь треугольника равна половине абсолютного значения 10 + 32 + 7 - 4 - 35 - 16, что равно 3. Количество переменных зависит от количества сторон многоугольника . Например, пятиугольник будет определен до x ₅ и y ₅ :

${\ displaystyle \ mathbf {A} _ {\ text {pent.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {4 } + x_ {4} y_ {5} + x_ {5} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {5 } г_ {4} -x_ {1} г_ {5} |}$

и четырехугольник будет определен до x ₄ и y ₄ :

${\ displaystyle \ mathbf {A} _ {\ text {quad.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {4 } + x_ {4} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {1} y_ {4} |.}$

Более сложный пример

Рассмотрим многоугольник, определяемый точками (3, 4), (5, 11), (12, 8), (9, 5) и (5, 6), как показано на диаграмме.

Площадь этого многоугольника:

${\ displaystyle {\ begin {align} \ mathbf {A} & = {1 \ over 2} \, {\ big |} 3 \ times 11 + 5 \ times 8 + 12 \ times 5 + 9 \ times 6 + 5 \ times 4 \\ & {} \ qquad {} -4 \ times 5-11 \ times 12-8 \ times 9-5 \ times 5-6 \ times 3 {\ big |} \\ [10pt] & = { 60 \ более 2} = 30. \ End {выровнено}}}$

Этимология

Причина, по которой эта формула называется формулой шнурка, заключается в том, что для ее оценки используется общий метод. В этом методе используются матрицы . В качестве примера выберите треугольник с вершинами (2, 4), (3, −8) и (1, 2). Затем постройте следующую матрицу, «обойдя» треугольник и закончив его начальной точкой.

${\ displaystyle {\ begin {bmatrix} 2 & 4 \\ 3 & -8 \\ 1 & 2 \\ 2 & 4 \ end {bmatrix}}}$

Сначала нарисуйте диагональ вниз и вправо косой чертой (как показано ниже),

  

и умножьте два числа, соединенных каждой косой чертой, затем сложите все произведения: (2 × −8) + (3 × 2) + (1 × 4) = −6. Сделайте то же самое с косой чертой по диагонали вниз и влево (показано ниже с косой чертой вниз):

  

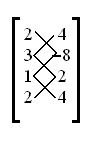
(4 × 3) + (−8 × 1) + (2 × 2) = 8. Затем возьмите абсолютную разность этих двух чисел: | (−6) - (8) | = 14. Уменьшение вдвое дает площадь треугольника: 7. Подобная организация чисел упрощает вспоминание и оценку формулы. Матрица со всеми прорисованными косыми чертами напоминает туфлю со шнурками, из-за чего происходит название алгоритма.

Обобщение

В более высоких измерениях площадь многоугольника может быть вычислена по его вершинам, используя форму внешней алгебры формулы Шнурка (например, в 3d, сумма последовательных перекрестных произведений ):

(когда вершины не компланарны, вычисляется векторная площадь, заключенная в петлю, то есть площадь проекции или «тень» в плоскости, в которой она наибольшая).

Эта формулировка также может быть обобщена для вычисления объема n-мерного многогранника по координатам его вершин или, точнее, по его гиперповерхностной сетке. Например, объем 3-мерного многогранника могут быть найдены с помощью триангуляции ее поверхности сетки и суммирование подписанных объемов на тетраэдров , образованной поверхности каждого треугольника и координат:

где сумма берется по граням, и нужно позаботиться о том, чтобы упорядочить вершины последовательно (все по часовой стрелке или против часовой стрелки, если смотреть снаружи многогранника). В качестве альтернативы выражение в терминах площадей граней и нормалей к поверхности может быть получено с помощью теоремы о расходимости (см. Многогранник § Объем ).

Смотрите также

• Планиметр
• Теорема Пика
• Формула Герона

внешние ссылки

• Видео математика о формуле шнурка Гаусса

использованная литература