Асимметрия - Skewness

Пример распределения с неотрицательной (положительной) асимметрией. Эти данные взяты из экспериментов по выращиванию ростков пшеницы.

В теории вероятностей и статистике , перекос является мерой асимметрии распределения вероятностей в виде реальной значной случайной величины около ее среднего. Значение асимметрии может быть положительным, нулевым, отрицательным или неопределенным.

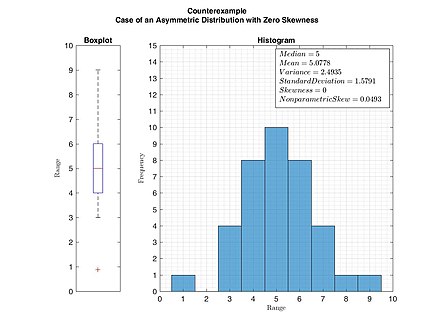
Для унимодального распределения отрицательный перекос обычно указывает, что хвост находится в левой части распределения, а положительный перекос указывает, что хвост находится справа. В случаях, когда один хвост длинный, а другой толстый, перекос не подчиняется простому правилу. Например, нулевое значение означает, что хвосты по обе стороны от среднего в целом уравновешиваются; это верно для симметричного распределения, но также может быть верно для асимметричного распределения, когда один хвост длинный и тонкий, а другой короткий, но толстый.

Вступление

Рассмотрим два распределения на рисунке ниже. На каждом графике значения на правой стороне распределения сужаются по-разному от значений на левой стороне. Эти сужающиеся стороны называются хвостами , и они предоставляют визуальные средства для определения того, какой из двух видов асимметрии имеет распределение:

1. отрицательный перекос : левый хвост длиннее; масса раздачи сосредоточена в правой части рисунка. Распределение называетсялевой перекос,левый хвост, илиперекос влево, несмотря на точто сама криваяпредставляется, искажены или наклоняясь вправо; leftвместо этого относится к вытянутому левому хвосту и, часто, среднее значение смещено влево от типичного центра данных. Распределение снаклономвлево обычно выглядит каккривая снаклоном вправо.
2. положительный перекос : правый хвост длиннее; масса раздачи сосредоточена в левой части рисунка. Распределение называетсяскошеннымвправо, справым хвостомилисмещением вправо, несмотря на то, что сама кривая кажется смещенной или наклоненной влево; Правовместо этого относится к вытянутому правому хвосту и, часто, к среднему значению, которое смещено вправо от типичного центра данных. Распределение снаклономвправо обычно выглядит каккривая снаклоном влево.

Асимметрия в ряду данных иногда может наблюдаться не только графически, но и при простой проверке значений. Например, рассмотрим числовую последовательность (49, 50, 51), значения которой равномерно распределены вокруг центрального значения 50. Мы можем преобразовать эту последовательность в отрицательно искаженное распределение, добавив значение намного ниже среднего, что, вероятно, является отрицательный выброс , например (40, 49, 50, 51). Следовательно, среднее значение последовательности становится 47,5, а медиана - 49,5. На основе формулы непараметрического перекоса , определяемого как перекос отрицательный. Точно так же мы можем сделать последовательность положительно искаженной, добавив значение, намного превышающее среднее значение, которое, вероятно, является положительным выбросом, например (49, 50, 51, 60), где среднее значение равно 52,5, а медиана - 50,5. ${\ Displaystyle (\ му - \ ню) / \ сигма,}$

Как упоминалось ранее, унимодальное распределение с нулевым значением асимметрии не означает, что это распределение обязательно симметрично. Однако симметричное одномодальное или мультимодальное распределение всегда имеет нулевую асимметрию.

Пример асимметричного распределения с нулевой асимметрией. Этот рисунок служит контрпримером, что нулевая асимметрия не обязательно означает симметричное распределение. (Асимметрия рассчитывалась по моментному коэффициенту асимметрии Пирсона.)

Отношение среднего и медианы

Асимметрия не связана напрямую с соотношением между средним и медианой: распределение с отрицательным перекосом может иметь среднее значение больше или меньше медианы, а также для положительного перекоса.

Общая взаимосвязь среднего и медианы при разно-искаженном унимодальном распределении

В старом понятии непараметрического перекоса , определяются как , где это среднее , является медианой , и представляет собой стандартное отклонение , коэффициент асимметрия определяются в терминах этих отношений: положительный / вправо непараметрические косые означает среднее больше , чем (вправо of) медианы, в то время как отрицательный / непараметрический перекос влево означает, что среднее значение меньше (слева от) медианы. Однако современное определение асимметрии и традиционное непараметрическое определение не всегда имеют один и тот же знак: хотя они совпадают для некоторых семейств распределений, они различаются в некоторых случаях, и их объединение вводит в заблуждение. ${\ Displaystyle (\ му - \ ню) / \ сигма,}$${\ displaystyle \ mu}$${\ displaystyle \ nu}$${\ displaystyle \ sigma}$

Если распределение симметрично , то среднее значение равно медиане, и распределение имеет нулевую асимметрию. Если распределение одновременно симметричное и одномодальное , то среднее значение = медиана = мода . Это случай подбрасывания монеты или серии 1,2,3,4, ... Обратите внимание, однако, что обратное неверно в целом, т.е. нулевая асимметрия (определенная ниже) не означает, что среднее значение равно к медиане.

В статье журнала 2005 года указывается:

Многие учебники учат практическому правилу, согласно которому среднее значение находится справа от медианы при наклоне вправо и слева от медианы при наклоне слева. Это правило с удивительной частотой не работает. Он может потерпеть неудачу в мультимодальных распределениях или в распределениях, где один хвост длинный, а другой тяжелый . Однако чаще всего правило не работает в дискретных распределениях, где площади слева и справа от медианы не равны. Такие распределения не только противоречат учебным отношениям между средним, медианой и перекосом, они также противоречат интерпретации медианы в учебниках.

Распределение взрослых жителей по домохозяйствам США

Например, в распределении взрослых жителей по домохозяйствам в США перекос вправо. Однако, поскольку в большинстве случаев меньше или равно моду, которая также является медианной, среднее значение находится в более тяжелом левом хвосте. В результате не удалось применить эмпирическое правило, согласно которому среднее значение находится справа от медианы при правом перекосе.

Определение

Коэффициент асимметрии момента Фишера

Асимметрия случайной величины X - это третий стандартизованный момент , определяемый как: ${\ displaystyle {\ tilde {\ mu}} _ {3}}$

${\ displaystyle {\ tilde {\ mu}} _ {3} = \ operatorname {E} \ left [\ left ({\ frac {X- \ mu} {\ sigma}} \ right) ^ {3} \ right ] = {\ frac {\ mu _ {3}} {\ sigma ^ {3}}} = {\ frac {\ operatorname {E} \ left [(X- \ mu) ^ {3} \ right]} { (\ operatorname {E} \ left [(X- \ mu) ^ {2} \ right]) ^ {3/2}}} = {\ frac {\ kappa _ {3}} {\ kappa _ {2} ^ {3/2}}}}$

где μ - среднее значение, σ - стандартное отклонение , E - оператор математического ожидания , μ ₃ - третий центральный момент , а κ _t - t -ые кумулянты . Иногда его называют моментным коэффициентом асимметрии Пирсона или просто моментным коэффициентом асимметрии , но его не следует путать с другими статистическими данными Пирсона (см. Ниже). Последнее равенство выражает асимметрию в терминах отношения третьего кумулянта κ ₃ к 1,5-й степени второго кумулянта κ ₂ . Это аналогично определению эксцесса как четвертого кумулянта, нормализованного квадратом второго кумулянта. Асимметрию также иногда обозначают Skew [ X ].

Если σ конечно, μ тоже конечно, и асимметрия может быть выражена через нецентральный момент E [ X ³ ], расширив предыдущую формулу,

${\ displaystyle {\ begin {align} {\ tilde {\ mu}} _ {3} & = \ operatorname {E} \ left [\ left ({\ frac {X- \ mu} {\ sigma}} \ right ) ^ {3} \ right] \\ & = {\ frac {\ operatorname {E} [X ^ {3}] - 3 \ mu \ operatorname {E} [X ^ {2}] + 3 \ mu ^ { 2} \ operatorname {E} [X] - \ mu ^ {3}} {\ sigma ^ {3}}} \\ & = {\ frac {\ operatorname {E} [X ^ {3}] - 3 \ mu (\ operatorname {E} [X ^ {2}] - \ mu \ operatorname {E} [X]) - \ mu ^ {3}} {\ sigma ^ {3}}} \\ & = {\ frac {\ operatorname {E} [X ^ {3}] - 3 \ mu \ sigma ^ {2} - \ mu ^ {3}} {\ sigma ^ {3}}}. \ end {align}}}$

Примеры

Асимметрия может быть бесконечной, как если бы

${\ displaystyle \ Pr \ left [X> x \ right] = x ^ {- 2} {\ mbox {for}} x> 1, \ \ Pr [X <1] = 0}$

где третьи кумулянты бесконечны, или когда

${\ displaystyle \ Pr [X <x] = (1-x) ^ {- 3} / 2 {\ mbox {для отрицательного}} x {\ mbox {and}} \ Pr [X> x] = (1+ x) ^ {- 3} / 2 {\ mbox {для положительного}} x.}$

где третий кумулянт не определен.

Примеры распределений с конечной асимметрией включают следующее.

• Нормальное распределение и любое другое симметричное распределение с конечным третьим моментом имеют асимметрию-
• Половины нормальное распределение имеет асимметрию чуть ниже 1
• Экспоненциальное распределение имеет асимметрию 2
• Распределение логнормального может иметь асимметрию любого положительного значения, в зависимости от его параметров

Асимметрия образца

Для выборки из n значений два естественных метода оценки моментов асимметрии совокупности:

${\ displaystyle b_ {1} = {\ frac {m_ {3}} {s ^ {3}}} = {\ frac {{\ tfrac {1} {n}} \ sum _ {i = 1} ^ { n} (x_ {i} - {\ overline {x}}) ^ {3}} {\ left [{\ tfrac {1} {n-1}} \ sum _ {i = 1} ^ {n} ( x_ {i} - {\ overline {x}}) ^ {2} \ right] ^ {3/2}}}}$

а также

${\ displaystyle g_ {1} = {\ frac {m_ {3}} {m_ {2} ^ {3/2}}} = {\ frac {{\ tfrac {1} {n}} \ sum _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {3}} {\ left [{\ tfrac {1} {n}} \ sum _ {i = 1} ^ { n} (x_ {i} - {\ overline {x}}) ^ {2} \ right] ^ {3/2}}},}$

где - среднее значение выборки , s - стандартное отклонение выборки , m ₂ - (смещенный) второй центральный момент выборки , а m ₃ - третий центральный момент выборки. ${\ displaystyle {\ overline {x}}}$

Другое распространенное определение асимметрии выборки :

${\ displaystyle {\ begin {align} G_ {1} & = {\ frac {k_ {3}} {k_ {2} ^ {3/2}}}} = {\ frac {n ^ {2}} {( n-1) (n-2)}} \; b_ {1} = {\ frac {\ sqrt {n (n-1)}} {n-2}} \; g_ {1}, \\\ конец {выровнено}}}$

где - уникальная симметричная несмещенная оценка третьего кумулянта и - симметричная несмещенная оценка второго кумулянта (т. е. выборочная дисперсия ). Этот скорректированный стандартизованный коэффициент момента Фишера – Пирсона является версией, которую можно найти в Excel и нескольких статистических пакетах, включая Minitab , SAS и SPSS . ${\ displaystyle k_ {3}}$${\ displaystyle k_ {2} = s ^ {2}}$${\ displaystyle G_ {1}}$

В предположении , что лежащая в основе случайной величина обычно распространяются, можно показать , что все три отношения , и являются объективными и последовательными оценками асимметрии населения , с , то есть, их распределения сходятся к нормальному распределению со средним 0 и дисперсией 6 ( Фишер, 1930). Таким образом, отклонение асимметрии образца приблизительно для достаточно больших образцов. Точнее, в случайной выборке размера n из нормального распределения, ${\ displaystyle X}$${\ displaystyle b_ {1}}$${\ displaystyle g_ {1}}$${\ displaystyle G_ {1}}$${\ displaystyle \ gamma _ {1} = 0}$${\ displaystyle {\ sqrt {n}} b_ {1} {\ xrightarrow {d}} N (0,6)}$${\ displaystyle 6 / n}$

${\ displaystyle \ operatorname {var} (G_ {1}) = {\ frac {6n (n-1)} {(n-2) (n + 1) (n + 3)}}.}$

В нормальных выборках имеет меньшую дисперсию из трех оценок, с ${\ displaystyle b_ {1}}$

${\ displaystyle \ operatorname {var} (b_ {1}) <\ operatorname {var} (g_ {1}) <\ operatorname {var} (G_ {1}).}$

Для не-нормальных распределений, , и , как правило , смещены оценки на асимметрии населения ; их ожидаемые значения могут даже иметь знак, противоположный истинной асимметрии. Например, смешанное распределение, состоящее из очень тонких гауссиан с центрами -99, 0,5 и 2 с весами 0,01, 0,66 и 0,33, имеет асимметрию примерно -9,77, но в выборке из 3 имеет ожидаемое значение примерно 0,32, поскольку обычно все три выборки находятся в положительной части распределения, которое искажено в другую сторону. ${\ displaystyle b_ {1}}$${\ displaystyle g_ {1}}$${\ displaystyle G_ {1}}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle G_ {1}}$

Приложения

Асимметрия - это описательная статистика, которую можно использовать вместе с гистограммой и нормальным графиком квантилей для характеристики данных или распределения.

Асимметрия указывает направление и относительную величину отклонения распределения от нормального распределения.

При выраженной асимметрии стандартные процедуры статистического вывода, такие как доверительный интервал для среднего, будут не только неверными в том смысле, что истинный уровень охвата будет отличаться от номинального (например, 95%) уровня, но они также приведут к неравенству. вероятности ошибок с каждой стороны.

Асимметрия может использоваться для получения приблизительных вероятностей и квантилей распределений (например, стоимости под риском в финансах) с помощью разложения Корниш-Фишера .

Многие модели предполагают нормальное распределение; т.е. данные симметричны относительно среднего. Нормальное распределение имеет нулевую асимметрию. Но на самом деле точки данных могут быть не идеально симметричными. Итак, понимание асимметрии набора данных показывает, будут ли отклонения от среднего положительными или отрицательными.

K-квадрат тест д'Агостина в это благость, из посадки теста нормальности на основе образца асимметрии и эксцесс образца.

Другие меры асимметрии

Сравнение среднего , медианы и моды двух логнормальных распределений с одинаковыми медианами и разными асимметриями.

Были использованы другие меры асимметрии, включая более простые вычисления, предложенные Карлом Пирсоном (не путать с моментным коэффициентом асимметрии Пирсона, см. Выше). Эти другие меры:

Первый коэффициент асимметрии Пирсона (асимметрия моды)

Асимметрия моды Пирсона или первый коэффициент асимметрии определяется как

среднее - режим/среднеквадратичное отклонение.

Второй коэффициент асимметрии Пирсона (медианная асимметрия)

Медианная асимметрия Пирсона или второй коэффициент асимметрии определяется как

3 ( среднее - медиана )/среднеквадратичное отклонение.

Это простое кратное непараметрическому перекосу .

Стоит отметить, что, поскольку асимметрия не связана с отношением порядка между модой, средним значением и медианой, знак этих коэффициентов не дает информации о типе асимметрии (влево / вправо).

Квантильные меры

Мера асимметрии Боули (с 1901 г.), также называемая коэффициентом Юла (с 1912 г.), определяется как:

${\ displaystyle B_ {1} = {\ frac {{\ frac {{{Q} _ {3}} + {{Q} _ {1}}} {2}} - {{Q} _ {2}} } {\ frac {{{Q} _ {3}} - {{Q} _ {1}}} {2}}} = {\ frac {{{Q} _ {3}} - 2 {{Q} _ {2} + {{Q} _ {1}}}} {{{Q} _ {3}} - {{Q} _ {1}}}}.}$

Числитель разница между средним верхней и нижней квартили (мера местоположения) и медиана (другой мерой местоположения), а знаменатель представляет собой полу-межквартильный диапазон , который для симметричных распределений является MAD с мерой дисперсии . ${\ displaystyle ({Q} _ {3}} - {{Q} _ {1}) / 2}$

Другие названия этой меры - мера асимметрии Гальтона, индекс Юла – Кендалла и квартиль асимметрии,

Более общая формулировка функции асимметрии была описана Groeneveld, RA и Meeden, G. (1984):

${\ displaystyle \ gamma (u) = {\ frac {F ^ {- 1} (u) + F ^ {- 1} (1-u) -2F ^ {- 1} (1/2)} {F ^ {-1} (u) -F ^ {- 1} (1-u)}}}$

где F - кумулятивная функция распределения . Это приводит к соответствующей общей мере асимметрии, определяемой как верхняя грань этого в диапазоне 1/2 ≤  u  <1. Другой показатель может быть получен путем интегрирования числителя и знаменателя этого выражения. Функция γ ( u ) удовлетворяет условию −1 ≤  γ ( u ) ≤ 1 и хорошо определена, не требуя наличия каких-либо моментов распределения. Меры асимметрии на основе квантилей на первый взгляд легко интерпретировать, но они часто показывают значительно большие вариации выборки, чем методы, основанные на моментах. Это означает, что часто выборки из симметричного распределения (например, равномерного распределения) случайно имеют большую квантильную асимметрию.

Мера асимметрии Боули - γ ( u ), оцененная при u  = 3/4. Для меры асимметрии Келли используется u = 0,1.

Коэффициент Греневельда и Медена

Греневельд и Меден предложили в качестве альтернативной меры асимметрии

${\ displaystyle B_ {3} = \ mathrm {skew} (X) = {\ frac {(\ mu - \ nu)} {E (| X- \ nu |)}},}$

где μ - среднее, ν - медиана, | ... | - абсолютное значение , а E () - оператор ожидания. По форме это тесно связано со вторым коэффициентом асимметрии Пирсона .

L-моменты

Использование L-моментов вместо моментов обеспечивает меру асимметрии, известную как L-асимметрия.

Асимметрия расстояния

Значение асимметрии, равное нулю, не означает, что распределение вероятностей является симметричным. Таким образом, существует потребность в другой мере асимметрии, обладающей этим свойством: такая мера была введена в 2000 году. Она называется асимметрией расстояния и обозначается dSkew. Если X - случайная величина, принимающая значения в d -мерном евклидовом пространстве, X имеет конечное ожидание, X ' является независимой идентично распределенной копией X и обозначает норму в евклидовом пространстве, тогда простая мера асимметрии относительно параметр местоположения θ равен ${\ displaystyle \ | \ cdot \ |}$

${\ displaystyle \ operatorname {dSkew} (X): = 1 - {\ frac {\ operatorname {E} \ | X-X '\ |} {\ operatorname {E} \ | X + X'-2 \ theta \ |}} {\ text {if}} \ Pr (X = \ theta) \ neq 1}$

и dSkew ( X ): = 0 для X  = θ (с вероятностью 1). Асимметрия расстояния всегда находится между 0 и 1, равна 0 тогда и только тогда, когда X диагонально симметрична относительно θ ( X и 2θ− X имеют одинаковое распределение вероятностей) и равна 1 тогда и только тогда, когда X является константой c ( ) с вероятность один. Таким образом, существует простой последовательный статистический тест диагональной симметрии, основанный на асимметрии выборочного расстояния : ${\ Displaystyle с \ neq \ theta}$

${\ displaystyle \ operatorname {dSkew} _ {n} (X): = 1 - {\ frac {\ sum _ {i, j} \ | x_ {i} -x_ {j} \ |} {\ sum _ { i, j} \ | x_ {i} + x_ {j} -2 \ theta \ |}}.}$

Medcouple

Medcouple является масштабно-инвариантной надежной мерой асимметрии, с точки пробоя 25%. Это медиана значений функции ядра

${\ displaystyle h (x_ {i}, x_ {j}) = {\ frac {(x_ {i} -x_ {m}) - (x_ {m} -x_ {j})} {x_ {i} - x_ {j}}}}$

взяты по всем парам таким образом, что , где - медиана выборки . Его можно рассматривать как медианное значение всех возможных мер квантильной асимметрии. ${\ displaystyle (x_ {i}, x_ {j})}$${\ Displaystyle х_ {я} \ geq x_ {m} \ geq x_ {j}}$${\ displaystyle x_ {m}}$ ${\ Displaystyle \ {x_ {1}, x_ {2}, \ ldots, x_ {n} \}}$

Смотрите также

• Пик Брэгга
• Coskewness
• Эксцесс
• Параметры формы
• Скошенное нормальное распределение
• Риск перекоса

использованная литература

Цитаты

Источники

внешние ссылки

• «Коэффициент асимметрии» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Коэффициент асимметрии для многомерных распределений Мишеля Петижана
• О более надежной оценке асимметрии и эксцесса Сравнение оценок перекоса Ким и Уайт.
• Замкнутые распределения - моделирование, инверсия и оценка параметров