Теорема Нильсена – Шрайера - Nielsen–Schreier theorem

В теории групп , раздел математики, то Нильсен-Шрайер теорема утверждает , что каждая подгруппа из свободной группы сама свободна. Он назван в честь Якоба Нильсена и Отто Шрайера .

Формулировка теоремы

Свободная группа может быть определена из группового представления, состоящего из набора генераторов без отношений. То есть каждый элемент является произведением некоторой последовательности образующих и их обратных, но эти элементы не подчиняются никаким уравнениям, кроме тех, которые тривиально следуют из gg ⁻¹ = 1. Элементы свободной группы можно описать как все возможные сокращенные слова , те цепочки генераторов и их обратных, в которых ни один генератор не смежен со своим собственным обратным. Два сокращенных слова можно умножить, объединив их и затем удалив любые пары генератор-инверсия, которые возникают в результате объединения.

Теорема Нильсена – Шрайера утверждает, что если H является подгруппой свободной группы G , то H сама изоморфна свободной группе. То есть, существует множество S элементов , которые генерируют H , без каких - либо нетривиальных соотношений между элементами S .

Формула Нильсена – Шрайера или формула индекса Шрайера количественно определяет результат в случае, когда подгруппа имеет конечный индекс: если G - свободная группа ранга n (свободная от n образующих), а H - подгруппа конечного индекса [ G  : H ] = e , то H не имеет ранга . ${\ Displaystyle 1 + е (п {-} 1)}$

Пример

Пусть G - свободная группа с двумя образующими , а H - подгруппа, состоящая из всех приведенных слов четной длины (произведений четного числа букв ). Тогда H порождается своими шестью элементами . Факторизация любого сокращенного слова в H на эти образующие, и их обратные могут быть построены просто путем взятия последовательных пар букв в сокращенном слове. Однако это не бесплатное представление H, потому что последние три генератора могут быть записаны в терминах первых трех как . Напротив, H порождается как свободная группа тремя элементами, между которыми нет отношений; или вместо этого несколькими другими тройками из шести генераторов. Кроме того, G свободна на n = 2 генераторах, H имеет индекс e = [ G  : H ] = 2 в G , а H свободен на 1 + e ( n –1) = 3 генераторах. Теорема Нильсена – Шрайера утверждает, что, как и H , любая подгруппа свободной группы может быть порождена как свободная группа, и если индекс группы H конечен, ее ранг определяется формулой индекса. ${\ displaystyle a, b}$${\ displaystyle a, b, a ^ {- 1}, b ^ {- 1}}$${\ Displaystyle p = aa, \ q = ab, \ r = ba, \ s = bb, \ t = ab ^ {- 1}, \ u = a ^ {- 1} b.}$${\ Displaystyle s = rp ^ {- 1} q, \ t = pr ^ {- 1}, \ u = p ^ {- 1} q}$${\ displaystyle p = aa, \ q = ab, \ r = ba,}$

Доказательство

Свободная группа G = π ₁ ( Х ) имеет п = 2 генераторы , соответствующие петли а , б от базовой точки Р в X . Подгруппа H слов четной длины с индексом e = [ G  : H ] = 2 соответствует покрывающему графу Y с двумя вершинами, соответствующими смежным классам H и H ' = aH = bH = a ⁻¹ H = b ^{- 1} H , и два приподнятых края для каждого из исходных краев петли a , b . Сжатие одного из ребер Y дает гомотопическую эквивалентность букету из трех окружностей, так что H = π ₁ ( Y ) - свободная группа с тремя образующими, например aa , ab , ba .

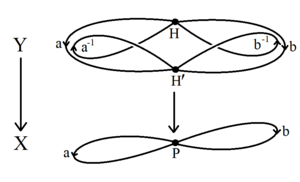
Короткое доказательство теоремы Нильсен-Шрейер использует алгебраическую топологию из основных групп и накрытий . Свободная группа G на множестве образующих - это фундаментальная группа букета окружностей , топологического графа X с единственной вершиной и петлей-ребром для каждой образующей. Любая подгруппа Н фундаментальной группы сам фундаментальной группы связного накрывающей Y → X. Пространство Y является (возможно , бесконечным) топологическим графом, то граф шрейерова смежного класса , имеющим одну вершины для каждого смежного класса в G / H . В любом подключенном топологического графа, то можно сжать края в остовного дерева графа, производя букет кругов , который имеет ту же основную группу H . Поскольку H - фундаментальная группа букета окружностей, она сама свободна.

Симплициальные гомологии позволяют вычислить ранг H , который равен h ₁ ( Y ), первому числу Бетти накрывающего пространства, количеству независимых циклов. Для G , не имеющего ранга n , граф X имеет n ребер и 1 вершину; в предположении, что H имеет конечный индекс [ G  : H ] = e , покрывающий граф Y имеет en ребер и e вершин. Первое число Бетти графа равно количеству ребер минус количество вершин плюс количество связанных компонентов; следовательно, ранг H равен:

${\ displaystyle h_ {1} (Y) \, = \, en-e + 1 \, = \, 1 + e (n {-} 1).}$

Это доказательство принадлежит Рейнхольду Бэру и Фридриху Леви  ( 1936 ); первоначальное доказательство с помощью Шрейер формирует график шрейеровского по-другому , как частное от деления графа Кэлей из G по модулю действия H .

Согласно лемме Шрайера о подгруппах , набор генераторов для свободного представления H может быть построен из циклов в покрывающем графе, образованном путем конкатенации пути остовного дерева от базовой точки (смежного класса идентичности) к одному из смежных классов, a единственное ребро, не являющееся деревом, и обратный путь остовного дерева от другой конечной точки ребра до базовой точки.

Аксиоматические основы

Хотя известно несколько различных доказательств теоремы Нильсена – Шрайера, все они зависят от выбранной аксиомы . Например, в доказательстве, основанном на фундаментальных группах букетов, аксиома выбора появляется в виде утверждения, что каждый связный граф имеет остовное дерево. Использование этой аксиомы необходимо, поскольку существуют модели теории множеств Цермело – Френкеля, в которых аксиома выбора и теорема Нильсена – Шрайера неверны. Теорема Нильсена – Шрайера, в свою очередь, влечет более слабую версию аксиомы выбора для конечных множеств.

История

Теорема Нильсена – Шрайера является неабелевым аналогом более старого результата Ричарда Дедекинда о том , что каждая подгруппа свободной абелевой группы является свободной абелевой .

Якоб Нильсен ( 1921 ) первоначально доказал ограниченную форму теоремы, утверждая, что любая конечно порожденная подгруппа свободной группы свободна. Его доказательство включает выполнение последовательности преобразований Нильсена на порождающем множестве подгруппы, которые уменьшают их длину (как сокращенные слова в свободной группе, из которой они взяты). Отто Шрайер доказал теорему Нильсена – Шрайера в ее полной общности в своей докторской диссертации 1926 года Die Untergruppen der freien Gruppe , также опубликованной в 1927 году в Abh. математика. Сем. Гамбург. Univ.

Топологическое доказательство, основанное на фундаментальных группах букетов кругов, принадлежит Рейнхольду Бэру и Фридриху Леви  ( 1936 ). Другой топологическое доказательство, основанное на теории Басса-Серра из групповых действий на деревьях , была опубликована Жан-Пьер Серр  ( 1970 ).

Смотрите также

• Основная теорема циклических групп , аналогичный результат для циклических групп, который в бесконечном случае можно рассматривать как частный случай теоремы Нильсена – Шрайера.

Примечания

использованная литература

• Баер, Рейнхольд ; Леви, Фридрих (1936), "Freie Produkte und ihre Untergruppen", Compositio Mathematica , 3 : 391–398.
• Фрид, Майкл Д .; Джарден, Моше (2008), Полевая арифметика , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 11 (3-е изд.), Springer-Verlag , p. 70, ISBN 978-3-540-77269-9, Zbl  1145,12001.
• Ховард, Пол Э. (1985), "Подгруппа свободной группы и аксиомы выбора", журнал символической логики , 50 (2): 458-467, DOI : 10,2307 / 2274234 , JSTOR  2274234 , MR  0793126.
• Джонсон, Д. Л. (1980), Темы теории представлений групп , серия лекций Лондонского математического общества, 42 , Cambridge University Press, ISBN 978-0-521-23108-4.
• Johnson, DL (1997), Presentations of Groups , Тексты студентов Лондонского математического общества, 15 (2-е изд.), Cambridge University Press, ISBN 978-0-521-58542-2.
• Läuchli, Hans (1962), "Auswahlaxiom in der Algebra", Commentarii Mathematici Helvetici , 37 : 1–18, doi : 10.1007 / bf02566957 , hdl : 20.500.11850 / 131689 , MR  0143705 , S2CID  186223589.
• Магнус, Вильгельм ; Каррасс, Авраам; Солитэр, Дональд (1976), комбинаторная теория групп (2-е пересмотренное издание), Dover Publications.
• Нильсен, Якоб (1921), "Om regning med ikke-kommutative faktorer og dens anvendelse i gruppeteorien", Math. Tidsskrift Б (Датский), +1921 : 78-94, СУЛ  48.0123.03.
• Ротман, Джозеф Дж. (1995), Введение в теорию групп , Тексты для выпускников по математике, 148 (4-е изд.), Springer-Verlag, ISBN 978-0-387-94285-8.
• Серр, Ж.-П. (1970), Groupes Discretes , Extrait de I'Annuaire du College de France, Париж.
• Серр, Ж.-П. (1980), Деревья , Springer-Verlag, ISBN 3-540-10103-9.
• Стиллвелл, Джон (1993), Классическая топология и комбинаторная теория групп , Тексты для выпускников по математике, 72 (2-е изд.), Springer-Verlag.