Машина Пост-Тьюринга - Post–Turing machine
Машина Пост является «рецептурой программы» из типа машины Тьюринга , содержащего вариант Эмил Post «с Тюрингу эквивалентной модели из расчета . Модель Поста и модель Тьюринга, хотя и очень похожи друг на друга, были разработаны независимо. Статья Тьюринга была получена для публикации в мае 1936 года, за ней последовала статья Поста в октябре.) Машина Пост-Тьюринга использует двоичный алфавит , бесконечную последовательность двоичных ячеек памяти и примитивный язык программирования с инструкциями для двунаправленного перемещения между хранилищами. расположение и изменение их содержимого по очереди. Названия «программа Пост-Тьюринга» и «машина Пост-Тьюринга» использовались Мартином Дэвисом в 1973–1974 годах (Davis 1973, p. 69ff). Позже, в 1980 году, Дэвис использовал название «программа Тьюринга – Поста» (Davis, in Steen, стр. 241).
1936: Пост-модель
В 1936 году статьи «Конечная комбинаторные процессы-композиция 1», Эмиль Post описал модель которой он высказал предположение является « логическим эквивалентом к рекурсивности ».
Модель вычислений Поста отличается от модели машины Тьюринга дальнейшей «атомизацией» действий, которые человеческий «компьютер» будет выполнять во время вычислений.
В модели Поста используется « пространство символов », состоящее из «двусторонней бесконечной последовательности пробелов или ящиков», каждый ящик может находиться в одном из двух возможных состояний, а именно «отмечен» (как один вертикальный штрих) и «немаркирован». " (пустой). Изначально помечено конечное количество ящиков, остальные не помечены. Затем «рабочий» должен перемещаться между ящиками, находясь внутри и работая только в одном ящике за раз, в соответствии с фиксированным конечным «набором направлений» ( инструкций ), которые нумеруются в порядке (1,2,3, ..., п ). Начиная с поля, «выделенного в качестве отправной точки», рабочий должен следовать набору инструкций по одной, начиная с инструкции 1.
Рабочий может выполнять пять различных примитивных операций:
- (а) Отметить коробку, в которой он находится, если она пуста
- (b) Стирание отметки в графе, в которой она находится, если она помечена
- (c) Переход к ящику справа
- (d) Переход к ящику слева от него.
- (e) Определение того, находится ли ящик, в котором он находится, промаркирован или нет.
Тогда i- е «направление» (указание), данное работнику, должно быть в одной из следующих форм:
- Выполните операцию O i [ O i = (a), (b), (c) или (d)], а затем следуйте направлению j i
- Выполните операцию (e) и в зависимости от ответа «да» или «нет» следуйте соответственно направлению j i ′ или j i ′ ′
- Стоп .
(Вышеупомянутый текст с отступом и курсивом такие же, как в оригинале.) Пост отмечает, что эта формулировка находится «на начальных этапах» разработки, и упоминает несколько возможностей «большей гибкости» в ее окончательной «окончательной форме», включая
- замена бесконечности ящиков конечным расширяемым пространством символов, «расширение примитивных операций для обеспечения необходимого расширения данного конечного пространства символов по мере продвижения процесса»,
- используя алфавит, состоящий более чем из двух символов, «имея более одного способа пометить квадрат»,
- введение конечного числа «физических объектов, служащих указателями, которые рабочий может идентифицировать и перемещать от коробки к коробке».
1947: Формальное сокращение Постом 5-кортежей Тьюринга до 4-х кортежей.
Как кратко упоминалось в статье Машина Тьюринга , Пост в своей статье 1947 года ( Рекурсивная неразрешимость проблемы Туэ ) раздробил 5-кортежи Тьюринга на 4-кортежи:
- «Наши четверки - это пятерки в развитии Тьюринга. То есть там, где наша стандартная инструкция заказывает печать (наложение) или движение, влево или вправо, стандартная инструкция Тьюринга всегда заказывает печать и движение вправо, влево или ничего» ( сноска 12, Неразрешимо , стр. 300)
Как и Тьюринг, он определил стирание как печать символа «S0». Таким образом, его модель допускала четверки только трех типов (см. Undecidable , p. 294):
- q i S j L q l ,
- q i S j R q l ,
- q i S j S k q l
В то время он все еще придерживался соглашения о машине состояний Тьюринга - он не формализовал понятие предполагаемого последовательного выполнения шагов до тех пор, пока конкретный тест символа не «разветвил» выполнение в другом месте.
1954, 1957: модель Ванга
Для еще большего сокращения - до четырех инструкций - модели Ванга, представленной здесь, см. Wang B-machine .
Ван (1957, но представленный ACM в 1954 году) часто цитируется (см. Мински (1967), стр. 200) как источник «программной формулировки» бинарных ленточных машин Тьюринга с использованием пронумерованных инструкций из набора
- написать 0
- написать 1
- двигай влево
- переместить вправо
- если сканирование 0, то перейти к инструкции i
- если сканирование 1, то перейти к инструкции j
Любую бинарную ленточную машину Тьюринга легко преобразовать в эквивалентную «программу Ванга» с помощью приведенных выше инструкций.
1974: первая модель Дэвиса
Мартин Дэвис был студентом Эмиля Поста. Вместе со Стивеном Клини он защитил докторскую диссертацию. под Алонзо Черчем (Дэвис (2000), 1-я и 2-я сноски, стр. 188).
Следующую модель он представил в серии лекций в Институте Куранта в Нью-Йоркском университете в 1973–1974 годах. Это модель, к которой Дэвис формально применил название «машина Пост-Тьюринга» с ее «языком Пост-Тьюринга». Предполагается, что инструкции выполняются последовательно (Davis 1974, стр. 71):
1978: вторая модель Дэвиса
Следующая модель представлена в виде эссе. Что такое вычисление? в Стин, страницы 241–267. По какой-то причине Дэвис переименовал свою модель в «машину Тьюринга – Поста» (с одним сдвигом назад на странице 256).
В следующей модели Дэвис присваивает цифры «1» «отметке / косой черте» Поста и «0» пустому квадрату. Процитируем Дэвиса: «Теперь мы готовы представить язык программирования Тьюринга – Поста. На этом языке есть семь видов инструкций:
- «ПЕЧАТЬ 1
- «ПЕЧАТЬ 0
- "НАПРАВО
- "ИДИ НАЛЕВО
- " ПЕРЕЙДИТЕ К ШАГУ i, ЕСЛИ 1 ОТКРЫТ
- " ПЕРЕЙДИТЕ К ШАГУ i, ЕСЛИ 0 СКАНИРУЕТСЯ
- "ОСТАНАВЛИВАТЬСЯ
«Программа Тьюринга-Поста представляет собой список инструкций, каждая из которых относится к одному из этих семи видов. Конечно, в реальной программе буква i в шаге пятого или шестого типа должна быть заменена на определенное (целое положительное) число ". (Дэвис в Steen, стр. 247).
1994 (2-е издание): Пост-Тьюринговая модель программы Дэвиса – Сигала – Вейукера.
«Хотя представленная нами формулировка Тьюринга ближе по духу к той, что была первоначально дана Эмилем Постом, именно анализ вычислений Тьюрингом сделал эту формулировку такой подходящей. Этот язык сыграл фундаментальную роль в теоретической информатике». (Дэвис и др. (1994) стр. 129)
Эта модель позволяет печатать несколько символов. Модель позволяет использовать B (пусто) вместо S 0 . Лента бесконечна в обоих направлениях. Либо голова, либо лента движутся, но их определения ВПРАВО и ВЛЕВО всегда указывают один и тот же результат в любом случае (Тьюринг использовал одно и то же соглашение).
- PRINT σ; Заменить отсканированный символ на σ
- IF σ GOTO L; IF отсканированный символ является σ THEN перейти к "первой" инструкции с меткой L
- ВПРАВО; Сканируйте квадрат сразу справа от сканируемого квадрата.
- ВЛЕВО; сканировать квадрат сразу слева от сканируемого в данный момент квадрата
Эта модель сводится к представленным выше двоичным версиям {0, 1}, как показано здесь:
- ПЕЧАТЬ 0 = УДАЛИТЬ; заменить отсканированный символ на 0 = B = ПУСТОЙ
- ПЕЧАТЬ 1; заменить отсканированный символ на 1
- IF 0 GOTO L; ЕСЛИ отсканированный символ равен 0 THEN перейти к "первой" инструкции с меткой L
- IF 1 GOTO L; ЕСЛИ отсканированный символ равен 1 THEN перейти к "первой" инструкции с меткой L
- ВПРАВО; Сканируйте квадрат сразу справа от сканируемого квадрата.
- ВЛЕВО; сканировать квадрат сразу слева от сканируемого в данный момент квадрата
Примеры машины Пост-Тьюринга
Распад пятерок Тьюринга на последовательность инструкций Пост-Тьюринга
Следующий метод «редукции» (декомпозиция, атомизация) - от 2-символьных 5-кортежей Тьюринга к последовательности 2-символьных инструкций Пост-Тьюринга - можно найти у Мински (1961). Он заявляет, что это сведение к « программе ... последовательности инструкций » находится в духе B-машины Хао Ванга (курсив в оригинале, ср. Minsky (1961), стр. 439).
(Сведение Мински к тому, что он называет «подпрограммой», приводит к 5, а не к 7 инструкциям Пост-Тьюринга. Он не атомизировал Wi0: «Записать символ Si0; перейти в новое состояние Mi0» и Wi1: «Записать символ Si1; перейти в новое состояние Mi1 ". Следующий метод дополнительно атомизирует Wi0 и Wi1; во всем остальном методы идентичны.)
Это сокращение 5-кортежей Тьюринга до инструкций Пост-Тьюринга может не привести к «эффективной» программе Пост-Тьюринга, но оно будет верным исходной программе Тьюринга.
В следующем примере каждый 5-кортеж Тьюринга занятого бобра с 2 состояниями преобразуется в
- начальный условный "переход" (goto, branch), за которым следует
- 2 инструкции по действию ленты для случая "0" - "Печать" или "Стереть" или "Нет", затем "Влево", "Вправо" или "Нет", а затем
- безусловный "переход" для случая "0" к его следующей инструкции
- 2 инструкции по действиям с лентой для случая "1" - "Печать" или "Стереть" или "Нет", затем "Влево", "Вправо" или "Нет", а затем
- безусловный «переход» для случая «1» к его следующей инструкции
всего 1 + 2 + 1 + 2 + 1 = 7 инструкций на одно состояние Тьюринга.
Например, состояние Тьюринга «А» занятого бобра с двумя состояниями, записанное в виде двух строк по 5 кортежей, выглядит следующим образом:
| Начальная m-конфигурация (состояние Тьюринга) | Лента символ | Операция печати | Движение ленты | Окончательная m-конфигурация (состояние Тьюринга) |
|---|---|---|---|---|
| А | 0 | п | р | B |
| А | 1 | п | L | B |
Таблица представляет собой только одну «инструкцию» Тьюринга, но мы видим, что она состоит из двух строк по 5 кортежей, одна для случая «символ ленты под заголовком = 1», а другая для случая «символ ленты под заголовком = 0. ". Тьюринг заметил ( Undecidable , p. 119), что два левых столбца - «m-конфигурация» и «символ» - представляют текущую «конфигурацию» машины - ее состояние, включая ленту и таблицу в этот момент, - и последние три столбца. его последующее «поведение». Поскольку машина не может находиться в двух «состояниях» одновременно, машина должна «перейти» либо к одной конфигурации, либо к другой:
| Исходная m-конфигурация и символ S | Операция печати | Движение ленты | Окончательная м-конфигурация |
|---|---|---|---|
| S = 0 → | P → | R → | B |
| → А < | |||
| S = 1 → | P → | L → | B |
После «ветви конфигурации» (J1 xxx) или (J0 xxx) машина следует одному из двух последующих «поведений». Мы перечисляем эти два поведения в одной строке и пронумеровываем (или маркируем) их последовательно (однозначно). Под каждым прыжком (ветвью, перейти) мы помещаем его "номер" перехода (адрес, местоположение):
Согласно соглашениям машины Пост-Тьюринга, каждая из инструкций Print, Erase, Left и Right состоит из двух действий:
- Действие ленты: {P, E, L, R}, затем
- Действие таблицы: перейти к следующей инструкции по порядку
И в соответствии с соглашениями машины Пост-Тьюринга условные «скачки» J0xxx, J1xxx состоят из двух действий:
- Действие ленты: посмотрите на символ на ленте под головой
- Действие таблицы: Если символ равен 0 (1) и J0 (J1), то перейдите к xxx, иначе перейдите к следующей инструкции по порядку
И согласно соглашениям машины Пост-Тьюринга безусловный "прыжок" Jxxx состоит из одного действия или, если мы хотим упорядочить последовательность из двух действий:
- Действие ленты: посмотрите на символ на ленте под головой
- Действие таблицы: Если символ равен 0, перейдите к xxx, иначе, если символ равен 1, перейдите к xxx.
Какие и сколько прыжков необходимы? Безусловный переход J xxx - это просто J0, за которым сразу следует J1 (или наоборот). Ван (1957) также показывает, что требуется только один условный переход, то есть либо J0 xxx, либо J1 xxx. Однако из-за этого ограничения на машине становится сложно писать инструкции. Часто используются только два, т.е.
- { J0 xxx, J1 xxx}
- { J1 xxx, J xxx}
- { J0 xxx, J xxx},
но использование всех трех { J0 xxx, J1 xxx, J xxx} действительно устраняет лишние инструкции. В примере с 2 состояниями Busy Beaver мы используем только { J1 xxx, J xxx}.
2-х штатный бобер
Задача занятого бобра - напечатать как можно больше бобров перед остановкой. Команда «Печать» записывает 1, команда «Стереть» (не используется в этом примере) записывает 0 (т. Е. То же самое, что и P0). Лента движется «влево» или «вправо» (т.е. «голова» неподвижна).
Таблица состояний для занятого бобра с двумя состояниями машины Тьюринга :
| Лента символ | Текущее состояние A | Текущее состояние B | ||||
|---|---|---|---|---|---|---|
| Написать символ | Переместить ленту | Следующее состояние | Написать символ | Переместить ленту | Следующее состояние | |
| 0 | 1 | р | B | 1 | L | А |
| 1 | 1 | L | B | 1 | N | ЧАС |
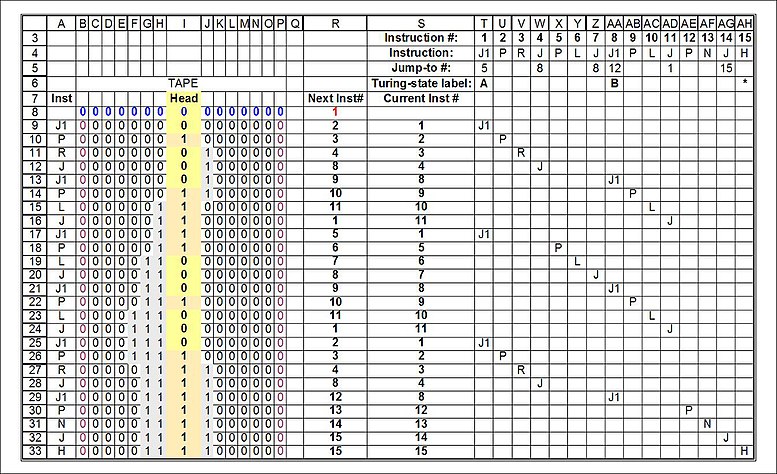
Инструкции для версии Пост-Тьюринга занятого бобра с двумя состояниями: обратите внимание, что все инструкции находятся в одной строке и в последовательности. Это существенное отличие от версии «Тьюринга» и имеет тот же формат, что и так называемая «компьютерная программа»:
| Инструкция # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Инструкция | J1 | п | р | J | п | L | J | J1 | п | L | J | п | N | J | ЧАС |
| Прыгать в # | 5 | 8 | 8 | 12 | 1 | 15 | |||||||||
| Метка состояния Тьюринга | А | B | ЧАС |
В качестве альтернативы мы можем записать таблицу в виде строки. Использование «разделителей параметров» «:» и разделителей инструкций «,» является полностью нашим выбором и не используется в модели. Условий нет (но см. Бут (1967), стр. 374, и Булос и Джеффри (1974, 1999), стр. 23), где можно найти некоторые полезные идеи о том, как комбинировать условные обозначения диаграммы состояний с инструкциями, т. Е. Использовать стрелки для обозначения место назначения прыжков). В приведенном ниже примере инструкции идут последовательно, начиная с «1», а параметры / «операнды» считаются частью их инструкций / «кодов операций»:
- J1: 5, P, R, J: 8, P, L, J: 8, J1: 12, P, L, J1: 1, P, N, J: 15, H
Примечания
использованная литература
- Стивен К. Клини , Введение в мета-математику, издательство North-Holland Publishing Company , Нью-Йорк, 10-е издание, 1991 г., впервые опубликовано в 1952 г. Глава XIII - превосходное описание машин Тьюринга; Клини использует в своем описании модель, похожую на Пост, и допускает, что модель Тьюринга может быть подвергнута дальнейшему дроблению, см. Сноску 1.
- Мартин Дэвис , редактор: The Undecidable, Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions , Raven Press, New York, 1965. Среди статей были статьи Гёделя , Черча , Россера , Клини и Поста.
- Мартин Дэвис , «Что такое вычисления», в « Математике сегодня» , Линн Артур Стин, Vintage Books (Random House), 1980. Замечательная маленькая статья, возможно, лучшая из когда-либо написанных о машинах Тьюринга. Дэвис сводит машину Тьюринга к гораздо более простой модели, основанной на модели вычислений Поста. Включает небольшую биографию Эмиля Поста.
- Мартин Дэвис , Вычислимость: с примечаниями Барри Джейкобса , Курантский институт математических наук, Нью-Йоркский университет, 1974.
- Мартин Дэвис , Рон Сигал , Элейн Дж. Вейкер , (1994) Вычислимость, сложность и языки: основы теоретической информатики - 2-е издание , Academic Press: Harcourt, Brace & Company, Сан-Диего, 1994 ISBN 0-12-206382- 1 (Первое издание, 1983 г.).
- Фред Хенни , Введение в вычислимость , Аддисон – Уэсли, 1977.
- Марвин Мински , (1961), Рекурсивная неразрешимость проблемы Поста о «теге» и других разделах теории машин Тьюринга , Annals of Mathematics, Vol. 74, No. 3, ноябрь 1961 г.
- Роджер Пенроуз , Новый разум императора: о компьютерах, умах и законах физики , Oxford University Press, Oxford England, 1990 (с исправлениями). Ср. Глава 2, «Алгоритмы и машины Тьюринга». Слишком сложное изложение (см. Статью Дэвиса для лучшей модели), но полное изложение машин Тьюринга и проблемы остановки , а также лямбда-исчисления Черча .
- Хао Ван (1957): «Вариант теории вычислительных машин Тьюринга», Журнал Ассоциации вычислительной техники (JACM) 4, 63–92.