Психология - Derangement

Количество возможных перестановок и нарушений n элементов. п ! ( n факториал) - количество n -перестановок; ! n ( n субфакториал) - это количество нарушений - n -перестановок, при которых все n элементов меняют свои начальные места.

Таблица значений
${\ displaystyle n}$	Перестановки, ${\ displaystyle n!}$	Психические расстройства, ${\ displaystyle! n}$	${\ displaystyle {\ frac {! n} {n!}}}$
0	1 = 1 × 10 0	1 = 1 × 10 0	= 1
1	1 = 1 × 10 0	0	= 0
2	2 = 2 × 10 0	1 = 1 × 10 0	= 0,5
3	6 = 6 × 10 0	2 = 2 × 10 0	≈0,33333 33333
4	24 = 2,4 × 10 1	9 = 9 × 10 0	= 0,375
5	120 = 1,20 × 10 2	44 = 4,4 × 10 1	≈0,36666 66667
6	720 = 7,20 × 10 2	265 = 2,65 × 10 2	≈0,36805 55556
7	5 040 = 5,04 × 10 3	1 854 ≈1,85 × 10 3	≈0,36785 71429
8	40 320 ≈4,03 × 10 4	14 833 ≈1,48 × 10 4	≈0,36788 19444
9	362 880 ≈3,63 × 10 5	133 496 ≈1,33 × 10 5	≈0,36787 91887
10	3 628 800 ≈3,63 × 10 6	1 334 961 ≈1,33 × 10 6	≈0,36787 94643
11	39 916 800 ≈3,99 × 10 7	14 684 570 ≈1,47 × 10 7	≈0,36787 94392
12	479 001 600 ≈4,79 × 10 8	176 214 841 ≈1,76 × 10 8	≈0,36787 94413
13	6 227 020 800 ≈6,23 × 10 9	2 290 792 932 ≈2,29 × 10 9	≈0,36787 94412
14	87 178 291 200 ≈8,72 × 10 10	32 071 101 049 ≈3,21 × 10 10	≈0,36787 94412
15	1 307 674 368 000 ≈1.31 × 10 12	481 066 515 734 ≈4,81 × 10 11	≈0,36787 94412
16	20 922 789 888 000 ≈2,09 × 10 13	7 697 064 251 745 ≈7,70 × 10 12	≈0,36787 94412
17	355 687 428 096 000 ≈3,56 × 10 14	130 850 092 279 664 ≈1.31 × 10 14	≈0,36787 94412
18	6 402 373 705 728 000 ≈6,40 × 10 15	2 355 301 661 033 953 ≈2,36 × 10 15	≈0,36787 94412
19	121 645 100 408 832 000 ≈1,22 × 10 17	44 750 731 559 645 106 ≈4,48 × 10 16	≈0,36787 94412
20	2 432 902 008 176 640 000 ≈2,43 × 10 18	895 014 631 192 902 121 ≈8,95 × 10 17	≈0,36787 94412
21 год	51 090 942 171 709 440 000 ≈5,11 × 10 19	18 795 307 255 050 944 540 ≈1,88 × 10 19	≈0,36787 94412
22	1 124 000 727 777 607 680 000 ≈1,12 × 10 21	413 496 759 611 120 779 881 ≈4,13 × 10 20	≈0,36787 94412
23	25 852 016 738 884 976 640 000 ≈2,59 × 10 22	9 510 425 471 055 777 937 262 ≈9,51 × 10 21	≈0,36787 94412
24	620 448 401 733 239 439 360 000 ≈6,20 × 10 23	228 250 211 305 338 670 494 289 ≈2,28 × 10 23	≈0,36787 94412
25	15 511 210 043 330 985 984 000 000 ≈1,55 × 10 25	5 706 255 282 633 466 762 357 224 ≈5,71 × 10 24	≈0,36787 94412
26 год	403 291 461 126 605 635 584 000 000 ≈4,03 × 10 26	148 362 637 348 470 135 821 287 825 ≈1,48 × 10 26	≈0,36787 94412
27	10 888 869 450 418 352 160 768 000 000 ≈1,09 × 10 28	4 005 791 208 408 693 667 174 771 274 ≈4,01 × 10 27	≈0,36787 94412
28 год	304 888 344 611 713 860 501 504 000 000 ≈3,05 × 10 29	112 162 153 835 443 422 680 893 595 673 ≈1,12 × 10 29	≈0,36787 94412
29	8 841 761 993 739 701 954 543 616 000 000 ≈8,84 × 10 30	3 252 702 461 227 859 257 745 914 274 516 ≈3,25 × 10 30	≈0,36787 94412
30	265 252 859 812 191 058 636 308 480 000 000 ≈2,65 × 10 32	97 581 073 836 835 777 732 377 428 235 481 ≈9,76 × 10 31	≈0,36787 94412

В комбинаторной математике , А психоз является перестановкой из элементов набора , таким образом, что ни один элемент не появляется в исходном положении. Другими словами, расстройство - это перестановка, не имеющая фиксированных точек .

Количество расстройств набора размера п известно как subfactorial из п или в n - й психоз числа или п - го де Монмор числа . Обозначения для часто используемых субфакториалов включают! n, D _n , d _n или n ¡.

Это можно показать! n равно ближайшему к n ! / e целому числу , где n ! обозначает факториал числа n, а e - число Эйлера .

Проблему подсчета отклонений впервые рассмотрел Пьер Раймон де Монморт в 1708 году; он решил ее в 1713 году, как и Николас Бернулли примерно в то же время.

Пример

Выделены 9 нарушений (из 24 вариантов).

Предположим, что профессор дал тест 4 студентам - A, B, C и D - и хочет, чтобы они оценили тесты друг друга. Конечно, ни один ученик не должен ставить оценку за свой тест. Сколькими способами профессор мог бы передать тесты студентам для выставления оценок, чтобы ни один студент не получил обратно свой тест? Из 24 возможных перестановок (4!) Для сдачи тестов,

ABCD ,	AB DC,	А CB D ,	CDB,	DBC,	A D C B,
BA CD ,	BADC ,	BCA D ,	BCDA ,	BDAC ,	BD C A,
КАБИНА D ,	CADB ,	C B A D ,	C B DA,	CDAB ,	CDBA ,
DABC ,	DA C B,	D B AC,	D BC A,	DCAB ,	DCBA .

всего 9 неисправностей (показаны выше синим курсивом). В каждой другой перестановке этого набора из 4-х членов по крайней мере один ученик получает обратно свой тест (выделенный жирным красным).

Другая версия проблемы возникает, когда мы спрашиваем количество способов, которыми n писем, адресованных разному человеку, могут быть помещены в n предварительно адресованных конвертов, чтобы ни одна буква не появлялась в конверте с правильным адресом.

Подсчет расстройств

Подсчет сбоев в наборе составляет проблему проверки шляпы , в которой учитывается количество способов, которыми n головных уборов (назовем их от h ₁ до h _n ) могут быть возвращены n людям (от P ₁ до P _n ) таким образом, чтобы не было шляпа возвращается к своему владельцу.

Каждый человек может получить любую из n  - 1 головных уборов, которые ему не принадлежат. Назовите ту шляпу, которая P ₁ получит h _i, и рассмотрите, что h _{i является} владельцем: P _i получает шляпу P ₁ , h ₁ или что-то другое. Соответственно, проблема распадается на два возможных случая:

1. P _i получает шляпу, отличную от h ₁ . Этот случай эквивалентен решению задачи с n  - 1 человеком и n  - 1 шляпами, потому что для каждого из n  - 1 человека, кроме P _1, есть ровно одна шляпа из оставшихся n  - 1 шляп, которые они могут не получить (для для любого P _j, кроме P _i , _{недопустимая} шляпа - h _j , а для P _i - h ₁ ).
2. P _i получает h ₁ . В этом случае задача сводится к п  - 2 -х человек и п  - 2 шляп, потому что P ₁ получил ч _я «s шляпа и P _я получил H ₁ » ы шляпу, эффективно поставив обоих из дальнейшего рассмотрения.

Для каждой из n  - 1 шляп, которые может получить P ₁ , количество способов, которыми P ₂ ,…, P _n могут все получить шляпы, является суммой подсчетов для двух случаев.

Это дает нам решение проблемы проверки шляпы: алгебраически сформулированное число! n неисправностей n -элементного множества равно

${\ Displaystyle! п = (п-1) ({! (п-1)} + {! (п-2)})}$для ,${\ Displaystyle п \ geq 2}$

где и . ${\ displaystyle! 0 = 1}$${\ displaystyle! 1 = 0}$

Количество неисправностей малой длины указано в таблице ниже.

Существуют различные другие выражения для! n , что эквивалентно приведенной выше формуле. Это включает

${\ Displaystyle! п = п! \ сумма _ {я = 0} ^ {п} {\ гидроразрыва {(-1) ^ {я}} {я!}}}$ для ${\ Displaystyle п \ geq 0}$

а также

${\ displaystyle! n = \ left [{\ frac {n!} {e}} \ right] = \ left \ lfloor {\ frac {n!} {e}} + {\ frac {1} {2}} \ right \ rfloor}$ для ${\ Displaystyle п \ geq 1,}$

где - ближайшая целочисленная функция, а - функция пола . ${\ Displaystyle \ влево [х \ вправо]}$${\ displaystyle \ left \ lfloor x \ right \ rfloor}$

Другие связанные формулы включают

${\ displaystyle! N = \ left \ lfloor {\ frac {n! +1} {e}} \ right \ rfloor, \ quad \ n \ geq 1,}$

${\ Displaystyle! N = \ left \ lfloor (e + e ^ {- 1}) n! \ right \ rfloor - \ lfloor en! \ rfloor, \ quad n \ geq 2,}$

а также

${\ displaystyle! n = n! - \ sum _ {i = 1} ^ {n} {n \ choose i} \ cdot {! (ni)}, \ quad \ n \ geq 1.}$

Также имеет место следующая рекуррентность:

${\ displaystyle! n = {\ begin {case} 1 & {\ text {if}} n = 0, \\ n \ left (! (n-1) \ right) + (- 1) ^ {n} & { \ text {if}} n> 0. \ end {case}}}$

Вывод по принципу включения – исключения

Можно также вывести нерекурсивную формулу для количества неисправностей n -множества. Ибо мы определяем набор перестановок n объектов, которые фиксируют k- й объект. Любое пересечение набора i этих множеств фиксирует конкретный набор i объектов и, следовательно, содержит перестановки. Есть такие коллекции, так что принцип включения-исключения дает ${\ Displaystyle 1 \ Leq К \ Leq N}$${\ displaystyle S_ {k}}$${\ displaystyle (ni)!}$${\ Displaystyle {п \ выбрать я}}$

${\ displaystyle {\ begin {align} | S_ {1} \ cup \ cdots \ cup S_ {n} | & = \ sum _ {i} \ left | S_ {i} \ right | - \ sum _ {i < j} \ left | S_ {i} \ cap S_ {j} \ right | + \ sum _ {i <j <k} \ left | S_ {i} \ cap S_ {j} \ cap S_ {k} \ right | + \ cdots + (- 1) ^ {n + 1} \ left | S_ {1} \ cap \ cdots \ cap S_ {n} \ right | \\ & = {n \ choose 1} (n-1) ! - {n \ choose 2} (n-2)! + {n \ choose 3} (n-3)! - \ cdots + (- 1) ^ {n + 1} {n \ choose n} 0! \ \ & = \ sum _ {i = 1} ^ {n} (- 1) ^ {i + 1} {n \ choose i} (ni)! \\ & = n! \ \ sum _ {i = 1} ^ {n} {(- 1) ^ {i + 1} \ over i!} \ end {выровнено}}}$

а поскольку расстройство - это перестановка, при которой ни один из n объектов не остается фиксированным, это означает, что

${\ displaystyle! n = n! - | S_ {1} \ cup \ cdots \ cup S_ {n} | = n! \ sum _ {i = 0} ^ {n} {\ frac {(-1) ^ { i}} {i!}}.}$

Рост количества неисправностей при приближении n к ∞

Из

${\ Displaystyle! п = п! \ сумма _ {я = 0} ^ {п} {\ гидроразрыва {(-1) ^ {я}} {я!}}}$

а также

${\ displaystyle e ^ {x} = \ sum _ {i = 0} ^ {\ infty} {x ^ {i} \ over i!}}$

при подстановке сразу получаем, что ${\ displaystyle \ textstyle x = -1}$

${\ displaystyle \ lim _ {n \ to \ infty} {! n \ over n!} = \ lim _ {n \ to \ infty} \ sum _ {i = 0} ^ {n} {\ frac {(- 1) ^ {i}} {i!}} = E ^ {- 1} \ приблизительно 0,367879 \ ldots.}$

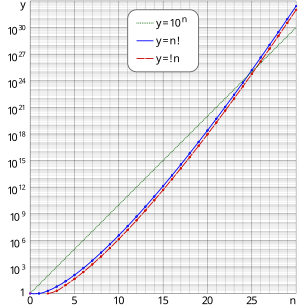
Это предел вероятности того, что случайно выбранная перестановка большого количества объектов является нарушением. Вероятность очень быстро сходится к этому пределу с увеличением n , вот почему! n - ближайшее к n ! / e целое число . Приведенный выше полулогарифмический график показывает, что граф неисправности отстает от графа перестановок почти на постоянное значение.

Более подробную информацию об этом вычислении и указанном выше ограничении можно найти в статье о статистике случайных перестановок .

Асимптотическое разложение по числам Белла.

Асимптотическое разложение числа сбоев по числам Белла выглядит следующим образом:

${\ displaystyle! n = {\ frac {n!} {e}} + \ sum _ {k = 1} ^ {m} \ left (-1 \ right) ^ {n + k-1} {\ frac { B_ {k}} {n ^ {k}}} + O \ left ({\ frac {1} {n ^ {m + 1}}} \ right),}$

где - любое фиксированное положительное целое число, а обозначает -е число Белла . Более того, константа, подразумеваемая большим O- членом, не превышает . ${\ displaystyle m}$${\ displaystyle B_ {k}}$${\ displaystyle k}$${\ displaystyle B_ {m + 1}}$

Обобщения

Задача des rencontres спрашивает, сколько перестановок набора размера n имеют ровно k неподвижных точек.

Расстройства - это пример более широкого поля ограниченных перестановок. Например, проблема мужского пола спрашивает , сидят ли за столом n пар противоположного пола мужчина-женщина-мужчина-женщина -..., сколькими способами они могут сидеть так, чтобы никто не сидел рядом со своим партнером?

Более формально, учитывая множества A и S , и некоторые наборы U и V из сюръекции → S , мы часто хотим знать число пар функций ( ф ,  г ) такая , что F в U и г в V , и для всех a в A , f ( a ) ≠ g ( a ); другими словами, где для любых f и g существует расстройство φ группы S такое, что f ( a ) = φ ( g ( a )).

Еще одно обобщение - следующая проблема:

Сколько существует анаграмм без фиксированных букв данного слова?

Например, для слова, состоящего только из двух разных букв, скажем, n букв A и m букв B, ответ, конечно, будет 1 или 0 в зависимости от того, n = m или нет, для единственного способа сформировать анаграмму без фиксированные буквы - это заменить все A на B , что возможно тогда и только тогда, когда n = m . В общем случае для слова из n ₁ букв X ₁ , n ₂ букв X ₂ , ..., n _r букв X _r оказывается (после правильного использования формулы включения-исключения ), что ответ имеет форма:

${\ displaystyle \ int _ {0} ^ {\ infty} P_ {n_ {1}} (x) P_ {n_ {2}} (x) \ cdots P_ {n_ {r}} (x) e ^ {- х} \, dx,}$

для некоторой последовательности многочленов P _n , где P _n имеет степень n . Но приведенный выше ответ для случая r = 2 дает соотношение ортогональности, откуда P _n являются многочленами Лагерра (с точностью до знака, который легко определяется).

${\ displaystyle \ int _ {0} ^ {\ infty} (t-1) ^ {z} e ^ {- t} dt}$ в комплексной плоскости.

В частности, для классических расстройств

${\ displaystyle! n = \ int _ {0} ^ {\ infty} (x-1) ^ {n} e ^ {- x} dx.}$

Вычислительная сложность

Это NP-полный, чтобы определить, содержит ли данная группа перестановок (описываемая данным набором перестановок, которые ее порождают) какие-либо нарушения.

использованная литература

внешние ссылки

• Баэз, Джон (2003). "Давайте психовать!" (PDF) .
• Bogart, Kenneth P .; Дойл, Питер Г. (1985). «Несексистское решение проблемы мужчин и женщин» .
• Дикау, Роберт М. "Диаграммы неисправностей" . Математические фигуры в системе Mathematica .
• Хассани, Мехди. «Нарушения и приложения» . Журнал целочисленных последовательностей (JIS), том 6, выпуск 1, статья 03.1.2, 2003 г.
• Weisstein, Эрик W . «Психология» . MathWorld - Интернет-ресурс Wolfram.