Cograph - Cograph

Граф Турана T (13,4), пример кографа

В теории графов , в кограф или комплемент-приводимого графа , или Р ₄ свободном от графика , представляет собой график , который может быть сформирован из одной вершины графа K ₁ по комплементации и несвязное объединение . То есть семейство кографов - это наименьший класс графов, включающий K ₁ и замкнутый относительно дополнения и дизъюнктного объединения.

Кографы были открыты независимо несколькими авторами с 1970-х годов; ранние ссылки включают Jung (1978) , Lerchs (1971) , Seinsche (1974) и Sumner (1974) . Их также называли D * -графами , наследственными графами Дейси (после родственной работы Джеймса К. Дейси-младшего по ортомодулярным решеткам ) и графами с 2-четностью . Они имеют простую структурную декомпозицию, включающую операции непересекающегося объединения и дополнения графов, которые могут быть кратко представлены помеченным деревом и используются алгоритмически для эффективного решения многих проблем, таких как поиск максимальной клики , которые трудно использовать для более общих классов графов.

Частные случаи кографов включают полные графы , полные двудольные графы , кластерные графы и пороговые графы . В cographs, в свою очередь, частные случаи расстояния наследственных графов , граф перестановка , сопоставимость графика и прекрасные графики .

Определение

Рекурсивная конструкция

Любой кограф может быть построен по следующим правилам:

любой граф с единственной вершиной является cograph;
если является копографом, значит, и его дополнительный граф ; ${\ displaystyle G}$ ${\ displaystyle {\ overline {G}}}$
если и являются кографами, то их несвязный союз - тоже . ${\ displaystyle G}$ ${\ displaystyle H}$ ${\ Displaystyle G \ чашка H}$

Кографы можно определить как графы, которые могут быть построены с использованием этих операций, начиная с графов с одной вершиной. В качестве альтернативы, вместо использования операции дополнения, можно использовать операцию соединения, которая состоит из формирования непересекающегося объединения и последующего добавления ребра между каждой парой вершины из и вершины из . ${\ Displaystyle G \ чашка H}$ ${\ displaystyle G}$ ${\ displaystyle H}$

Другие характеристики

Можно дать несколько альтернативных характеристик кографов. Среди них:

Кограф - это граф, который не содержит пути P ₄ на 4 вершинах (и, следовательно, длины 3) в качестве индуцированного подграфа . То есть граф является кографом тогда и только тогда, когда для любых четырех вершин , если и являются ребрами графа, то по крайней мере одно из или также является ребром. ${\ displaystyle v_ {1}, v_ {2}, v_ {3}, v_ {4}}$ ${\ Displaystyle \ {v_ {1}, v_ {2} \}, \ {v_ {2}, v_ {3} \}}$ ${\ displaystyle \ {v_ {3}, v_ {4} \}}$ ${\ Displaystyle \ {v_ {1}, v_ {3} \}, \ {v_ {1}, v_ {4} \}}$ ${\ displaystyle \ {v_ {2}, v_ {4} \}}$
Кограф - это граф, все индуцированные подграфы которого обладают тем свойством, что любая максимальная клика пересекает любое максимальное независимое множество в одной вершине.
Кограф - это граф, в котором каждый нетривиальный индуцированный подграф имеет не менее двух вершин с одинаковыми окрестностями.
Кограф - это граф, в котором каждый связный индуцированный подграф имеет несвязное дополнение.
Кограф - это граф, все связные индуцированные подграфы которого имеют диаметр не более 2.
Кограф - это граф, в котором каждая компонента связности является дистанционно-наследственным графом с диаметром не более 2.
Кограф - это граф с шириной клики не более 2.
Кограф является сопоставимость графа из частичного порядка последовательно-параллельно .
Кограф является графом перестановкой из сепарабельной перестановки .
Кограф - это граф, все минимальные хордовые пополнения которого являются тривиально совершенными графами .
Кограф - это наследственно хорошо раскрашенный граф , такой граф, в котором каждая жадная раскраска каждого индуцированного подграфа использует оптимальное количество цветов.
Граф является кографом тогда и только тогда, когда каждый порядок вершин графа является совершенным порядком , поскольку отсутствие P ₄ означает, что никакое препятствие на пути к совершенному порядку не будет существовать ни в каком порядке вершин.

Cotrees

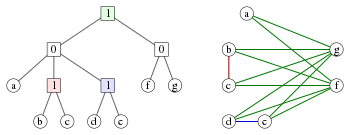
Cotree и соответствующий cograph. Каждое ребро ( u , v ) в cograph имеет цвет, соответствующий наименьшему общему предку u и v в cotree.

Cotree представляет собой дерево , в котором внутренние узлы обозначены с номерами 0 и 1. Каждый cotree Т определяет кограф G , имеющие листы T в качестве вершин, и в котором поддерево с корнем в каждом узле Т соответствует индуцированному подграфу в G определяется набором листьев, спускающихся с этого узла:

Поддерево, состоящее из единственного листового узла, соответствует индуцированному подграфу с единственной вершиной.
Поддерево с корнем в узле с меткой 0 соответствует объединению подграфов, определенных дочерними элементами этого узла.
Поддерево с корнем в узле с меткой 1 соответствует объединению подграфов, определенных дочерними элементами этого узла; то есть мы формируем объединение и добавляем ребро между каждыми двумя вершинами, соответствующими листам в разных поддеревьях. В качестве альтернативы объединение набора графов можно рассматривать как сформированное путем дополнения каждого графа, формирования объединения дополнений и последующего дополнения полученного объединения.

Эквивалентный способ описания cograph, образованного из cotree, состоит в том, что две вершины соединены ребром тогда и только тогда, когда самый младший общий предок соответствующих листьев помечен цифрой 1. И наоборот, каждый cograph может быть представлен таким образом cotree . Если мы требуем, чтобы метки на любом пути корневого листа этого дерева чередовались между 0 и 1, это представление будет уникальным.

Вычислительные свойства

Кографы могут быть распознаны за линейное время и построено представление дочернего дерева с использованием модульной декомпозиции , уточнения разбиения , LexBFS или разбиения декомпозиции . После того, как представление cotree построено, многие знакомые проблемы с графами могут быть решены с помощью простых вычислений снизу вверх на cotree.

Например, чтобы найти максимальную клику в cograph, вычислите в восходящем порядке максимальную клику в каждом подграфе, представленном поддеревом cotree. Для узла с меткой 0 максимальная клика является максимальной среди клик, вычисленных для дочерних узлов этого узла. Для узла с меткой 1 максимальная клика представляет собой объединение клик, вычисленных для дочерних узлов этого узла, и имеет размер, равный сумме размеров дочерних клик. Таким образом, поочередно максимизируя и суммируя значения, хранящиеся в каждом узле cotree, мы можем вычислить максимальный размер клики, а поочередно максимизируя и принимая объединения, мы можем построить саму максимальную клику. Подобные вычисления дерева снизу вверх позволяют вычислить максимальное независимое множество , число раскраски вершин , максимальное покрытие клик и гамильтоничность (то есть существование гамильтонова цикла ) за линейное время из представления cotree кографа. Поскольку кографы имеют ограниченную ширину клики, теорема Курселя может использоваться для проверки любого свойства в монадической логике графов второго порядка (MSO ₁ ) на кографах за линейное время.

Проблема проверки того, находится ли данный граф на расстоянии k вершин и / или t ребер от кографа, решаема с фиксированным параметром . Решение о том, можно ли удалить граф по k- краю из кографа, можно решить за O ^* (2,415 ^k ) времени и отредактировать по k- краю до кографа за O ^* (4,612 ^k ). Если самый большой индуцированный подграф графа графа может быть найден путем удаления k вершин из графа, он может быть найден за время O ^* (3,30 ^k ).

Два кографа изоморфны тогда и только тогда, когда их родословные (в канонической форме без двух смежных вершин с одинаковой меткой) изоморфны. Из-за этой эквивалентности можно определить за линейное время, изоморфны ли два кографа, построив их дочерние деревья и применив тест изоморфизма линейного времени для помеченных деревьев.

Если H - индуцированный подграф кографа G , то H сам является кографом; cotree для H может быть сформирован путем удаления некоторых листьев из cotree для G и затем подавления узлов, у которых есть только один дочерний элемент . Из теоремы Крускала о дереве следует, что отношение быть индуцированным подграфом является хорошо квазиупорядочением на кографах. Таким образом, если подсемейство кографов (например, планарных кографов) замкнуто относительно операций индуцированного подграфа, то оно имеет конечное число запрещенных индуцированных подграфов . С вычислительной точки зрения это означает, что проверка принадлежности к такому подсемейству может выполняться за линейное время, используя восходящее вычисление на дереве заданного графа, чтобы проверить, содержит ли он какой-либо из этих запрещенных подграфов. Однако, когда размеры двух кографов являются переменными, проверка того, является ли один из них индуцированным подграфом другого, является NP-полной .

Кографы играют ключевую роль в алгоритмах распознавания функций с однократным чтением .

Перечисление

Количество связанных кографов с n вершинами для n = 1, 2, 3, ... равно:

1, 1, 2, 5, 12, 33, 90, 261, 766, 2312, 7068, 21965, 68954, ... (последовательность A000669 в OEIS )

При n > 1 существует одинаковое количество несвязных кографов, потому что для каждого кографа связан ровно один из них или его дополнительный граф .

Связанные семейства графов

Подклассы

Каждый полный граф $K n$ является копографом, чье дерево состоит из одного узла и $n$ листьев. Аналогично, всякий полный двудольный граф $K a, b$ является копографом. Его cotree укоренен в 1-узле , который имеет два 0-узел детей, один с $через$ лист детьми и один с $б$ детьми листьев. Турана график может быть сформирован путем объединения семейства равного размера независимых множеств; таким образом, это также cograph, cotree которого базируется на 1-узле, который имеет дочерний 0-узел для каждого независимого набора.

Каждый график пороговых значений также является графом . Пороговый граф может быть сформирован путем многократного добавления одной вершины, либо связанной со всеми предыдущими вершинами, либо ни с одной из них; каждая такая операция является одной из операций непересекающегося объединения или соединения, посредством которых может быть образовано cotree.

Суперклассы

Характеристика кографов тем свойством, что каждая клика и максимальное независимое множество имеют непустое пересечение, является более сильной версией определяющего свойства сильно совершенных графов , в котором каждый индуцированный подграф содержит независимое множество, пересекающее все максимальные клики. В кографе каждое максимальное независимое множество пересекает все максимальные клики. Таким образом, каждый кограф абсолютно совершенен.

Тот факт, что кографы не содержат P _4, означает, что их можно легко заказать . Фактически, каждый порядок вершин кографа является совершенным порядком, что дополнительно подразумевает, что максимальное нахождение клики и минимальная раскраска могут быть найдены за линейное время с любой жадной раскраской и без необходимости в декомпозиции cotree.

Каждый cograph является дистанционно-наследственным графом , что означает, что любой индуцированный путь в cograph является кратчайшим путем . Кографы могут быть охарактеризованы среди дистанционно-наследственных графов как имеющие диаметр два в каждом компоненте связности. Каждый кограф также сопоставимость графики , из частичного порядка последовательно-параллельно , полученного путем замены несвязных и присоединиться к операции , с помощью которого кограф была построена несвязным объединением и порядковыми суммы операциями на частичных порядках. Поскольку сильно совершенные графы, идеально упорядочиваемые графы, графы с дистанционной наследственностью и графы сопоставимости - все это совершенные графы , кографы также идеальны.

Languages

In other projects