Бинарный алгоритм GCD - Binary GCD algorithm

Визуализация использования двоичного алгоритма НОД для нахождения наибольшего общего делителя (НОД) 36 и 24. Таким образом, НОД составляет 2 2 × 3 = 12.

Бинарный алгоритм НОДА , также известный как алгоритм Штейна или бинарный алгоритм Евклида , алгоритм , который вычисляет наибольший общий делитель двух целых неотрицательных чисел. Алгоритм Штейна использует более простые арифметические операции, чем традиционный алгоритм Евклида ; он заменяет деление арифметическим сдвигом , сравнением и вычитанием.

Хотя алгоритм в его современной форме был впервые опубликован израильским физиком и программистом Йозефом Штейном в 1967 году, он, возможно, был известен во 2 веке до нашей эры в древнем Китае.

Алгоритм

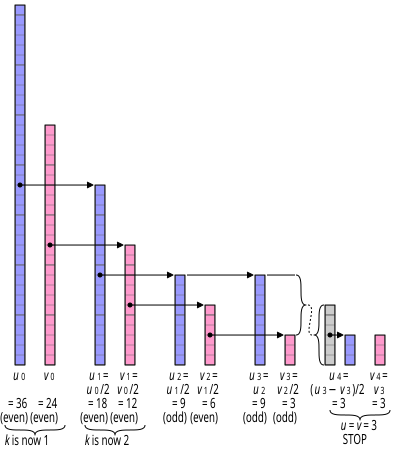
Алгоритм уменьшает проблему нахождения НОД двух неотрицательных чисел v и u , многократно применяя эти тождества:

  • gcd (0, v ) = v , потому что все делит ноль, а v - наибольшее число, которое делит v . Аналогично gcd ( u , 0) =  u .
  • gcd ( 2u ,  2v ) = 2 · gcd ( u , v )
  • gcd ( 2u ,  v ) = gcd ( u ,  v ), если v нечетно (2 не является общим делителем). Аналогично, gcd ( u ,  2v ) = gcd ( u ,  v ), если u нечетное.
  • gcd ( u ,  v ) = gcd (| u  -  v |, min ( u , v )), если u и v оба нечетные.

Реализация

Хотя приведенное выше описание алгоритма является математически правильным, эффективные программные реализации обычно отличаются от него несколькими заметными способами:

  • отказ от пробного деления на 2 в пользу одинарного битового сдвига и примитива нулей в конце счета ; это функционально эквивалентно многократному применению тождества 3, но намного быстрее;
  • выражение алгоритма итеративно, а не рекурсивно : результирующая реализация может быть выложена так, чтобы избежать повторной работы, вызывая идентификатор 2 в начале и поддерживая в качестве инварианта, что оба числа являются нечетными при входе в цикл, что необходимо только для реализации идентификаторов 3 и 4;
  • освобождение тела цикла от ветвей, за исключением его условия выхода ( v == 0 ): в приведенном ниже примере обмен u и v (гарантирующий, что u ≤ v ) сводится к условным ходам ; трудно предсказуемые ветви могут иметь большое негативное влияние на производительность.

Ниже приведена реализация алгоритма на Rust, иллюстрирующая эти различия, адаптированная из uutils : 

pub fn gcd(mut u: u64, mut v: u64) -> u64 {
    use std::cmp::min;
    use std::mem::swap;

    // Base cases: gcd(n, 0) = gcd(0, n) = n
    if u == 0 {
        return v;
    } else if v == 0 {
        return u;
    }

    // Using identities 2 and 3:
    // gcd(2ⁱ u, 2ʲ v) = 2ᵏ gcd(u, v) with u, v odd and k = min(i, j)
    // 2ᵏ is the greatest power of two that divides both u and v
    let i = u.trailing_zeros();  u >>= i;
    let j = v.trailing_zeros();  v >>= j;
    let k = min(i, j);

    loop {
        // u and v are odd at the start of the loop
        debug_assert!(u % 2 == 1, "u = {} is even", u);
        debug_assert!(v % 2 == 1, "v = {} is even", v);

        // Swap if necessary so u <= v
        if u > v {
            swap(&mut u, &mut v);
        }

        // Using identity 4 (gcd(u, v) = gcd(|v-u|, min(u, v))
        v -= u;

        // Identity 1: gcd(u, 0) = u
        // The shift by k is necessary to add back the 2ᵏ factor that was removed before the loop
        if v == 0 {
            return u << k;
        }

        // Identity 3: gcd(u, 2ʲ v) = gcd(u, v) (u is known to be odd)
        v >>= v.trailing_zeros();
    }
}

Эффективность

Алгоритм требует O ( n ) шагов, где n - количество бит в большем из двух чисел, так как каждые 2 шага уменьшают хотя бы один из операндов как минимум в 2 раза. Каждый шаг включает только несколько арифметических действий. операции (O (1) с малой константой); при работе с числами размером со слово каждая арифметическая операция преобразуется в одну машинную операцию, поэтому количество машинных операций порядка log₂ (max ( u , v )), то есть n .

Однако асимптотическая сложность этого алгоритма составляет O (n 2 ), поскольку каждая из этих арифметических операций (вычитание и сдвиг) занимает линейное время для чисел произвольного размера (одна машинная операция на слово представления). Это то же самое, что и для алгоритма Евклида, хотя более точный анализ, проведенный Ахави и Валле, показал, что двоичный НОД использует примерно на 60% меньше битовых операций.

Расширения

Бинарный алгоритм GCD может быть расширен несколькими способами: либо для вывода дополнительной информации, более эффективной работы с произвольно большими целыми числами , либо для вычисления GCD в областях, отличных от целых.

Расширенный двоичный НОД алгоритм, аналогичный расширенному алгоритм Евклида , помещается в первом роде расширение, так как она обеспечивает коэффициенты Беза в дополнении к НОДУ, то есть целые числа и Ь таким образом, что а • и + Ь · V = НОД ( u , v ).

В случае больших целых чисел наилучшая асимптотическая сложность - O (log n M ( n )), где M ( n ) - стоимость n- битного умножения; это почти линейно и значительно меньше, чем O (n 2 ) двоичного алгоритма GCD, хотя конкретные реализации превосходят старые алгоритмы только для чисел, превышающих примерно 64 килобит ( т. е. больше 8 × 10 19265 ). Это достигается расширением двоичного алгоритма НОД с использованием идей алгоритма Шёнхаге – Штрассена для быстрого целочисленного умножения.

Алгоритм двоичного НОДА также был распространен и на другие , чем натуральные числа, такие как домены гауссовых целых числа , Эйзенштейн целых числа , квадратичные кольца и произвольными уникальные домены факторизации .

Историческое описание

Алгоритм вычисления НОД двух чисел был известен в древнем Китае при династии Хань как метод уменьшения дробей:

Если возможно, уменьшите его вдвое; в противном случае возьмите знаменатель и числитель, вычтите меньшее из большего и сделайте это поочередно, чтобы сделать их одинаковыми. Уменьшить на такое же количество.

-  Fangtian - Геодезия, Девять глав по математическому искусству

Фраза "если можно, разделить вдвое" неоднозначна,

  • если это применимо, когда любое из чисел становится четным, алгоритм является двоичным алгоритмом НОД;
  • если это применимо только тогда, когда оба числа четные, алгоритм аналогичен алгоритму Евклида .

Смотрите также

использованная литература

  1. ↑ Брент, Ричард П. (13–15 сентября 1999 г.). Двадцатилетний анализ двоичного алгоритма Евклида . Симпозиум Оксфорд-Майкрософт 1999 г. в честь профессора сэра Энтони Хора. Оксфорд.
  2. ↑ Брент, Ричард П. (ноябрь 1999 г.). Дальнейший анализ двоичного алгоритма Евклида (Технический отчет). Вычислительная лаборатория Оксфордского университета. arXiv : 1303.2772 . ПРГ ТР-7-99.
  3. ^ Stein, J. (февраль 1967), "Вычислительные проблемы, связанные с алгеброй Рака", Журнал вычислительной физики , 1 (3): 397-405, Bibcode : 1967JCoPh ... 1..397S , doi : 10.1016 / 0021- 9991 (67) 90047-2 , ISSN  0021-9991
  4. ^ a b Кнут, Дональд (1998), получисловые алгоритмы , Искусство компьютерного программирования , 2 (3-е изд.), Addison-Wesley, ISBN 978-0-201-89684-8
  5. ^ a b Чжан, Шаохуа (05.10.2009). «Понятие о простых числах и алгоритм вычисления наибольшего общего делителя в Древнем Китае». arXiv : 0910.0095 [ math.HO ].
  6. ^ Godbolt, Мэтт. "Обозреватель компилятора" . Проверено 10 июля 2021 года .
  7. ↑ Капур, Раджив (21 февраля 2009 г.). «Как избежать затрат на неверное предсказание отрасли» . Зона разработчиков Intel .
  8. ^ Лемир, Даниэль (2019-10-15). «Неправильно предсказанные ветви могут увеличить время работы» .
  9. ^ «GNU MP 6.1.2: двоичный GCD» .
  10. ^ Ахави, Али; Валле, Бриджит (2000), «Средняя битовая сложность евклидовых алгоритмов» , Proceedings ICALP'00, Lecture Notes Computer Science 1853 : 373–387, CiteSeerX  10.1.1.42.7616
  11. Перейти ↑ Knuth 1998 , p. 646, ответ на упражнение 39 раздела 4.5.2.
  12. ^ Менезес, Альфред Дж .; van Oorschot, Paul C .; Ванстон, Скотт А. (октябрь 1996 г.). «§14.4 алгоритмы наибольшего общего делителя» (PDF) . Справочник по прикладной криптографии . CRC Press. С. 606–610. ISBN 0-8493-8523-7. Проверено 9 сентября 2017 .
  13. ^ Коэн, Анри (1993). «Глава 1: Основные теоретико-числовые алгоритмы». Курс вычислительной алгебраической теории чисел . Тексты для выпускников по математике . 138 . Springer-Verlag . С. 17–18. ISBN 0-387-55640-0.
  14. ^ Stehlé, Дэмиен; Циммерманн, Пауль (2004), "Бинарный рекурсивный алгоритм НОД" (PDF) , Алгоритмическая теория чисел , Конспект лекций в Comput. Sci . , 3076 ., Springer, Berlin, стр 411-425, CiteSeerX  10.1.1.107.8612 , DOI : 10.1007 / 978-3-540-24847-7_31 , ISBN 978-3-540-22156-2, MR  2138011 , Отчет об исследовании INRIA RR-5050.
  15. ^ Weilert, Андре (июль 2000). «(1 + i) -арное вычисление НОД в Z [i] как аналог двоичного алгоритма НОД» . Журнал символических вычислений . 30 (5): 605–617. DOI : 10,1006 / jsco.2000.0422 .
  16. ^ Дамгард, Иван Бьерре; Франдсен, Гудмунд Сковбьерг (12–15 августа 2003 г.). Эффективные алгоритмы НОД и кубической остаточности в кольце целых чисел Эйзенштейна . 14-й Международный симпозиум по основам теории вычислений. Мальмё , Швеция . С. 109–117. DOI : 10.1007 / 978-3-540-45077-1_11 .CS1 maint: формат даты ( ссылка )
  17. ↑ Агарвал, Саураб; Франдсен, Гудмунд Сковбьерг (13–18 июня 2004 г.). Бинарные НОД-подобные алгоритмы для некоторых комплексных квадратичных колец . Симпозиум по алгоритмической теории чисел. Берлингтон, штат Вирджиния , США. С. 57–71. DOI : 10.1007 / 978-3-540-24847-7_4 .CS1 maint: формат даты ( ссылка )
  18. ↑ Агарвал, Саураб; Франдсен, Гудмунд Сковбьерг (20–24 марта 2006 г.). Новый алгоритм НОД для квадратичных колец чисел с уникальной факторизацией . 7-й латиноамериканский симпозиум по теоретической информатике. Вальдивия, Чили . С. 30–42. DOI : 10.1007 / 11682462_8 .CS1 maint: формат даты ( ссылка )
  19. ^ Wikström, Дуглас (11-15 июля 2005). Об l-арном НОД-алгоритме в кольцах целых чисел . Автоматы, языки и программирование, 32-й международный коллоквиум. Лиссабон , Португалия . С. 1189–1201. DOI : 10.1007 / 11523468_96 .CS1 maint: формат даты ( ссылка )

дальнейшее чтение

Охватывает расширенный двоичный НОД и вероятностный анализ алгоритма.

Охватывает множество тем, включая расширенный алгоритм двоичного НОД, который выводит коэффициенты Безу , эффективную обработку целых чисел с разной точностью с использованием варианта алгоритма НОД Лемера и взаимосвязь между НОД и разложениями действительных чисел в непрерывную дробь .

Анализ алгоритма в среднем случае, через призму функционального анализа : основные параметры алгоритмов отлиты как динамической системы , и их среднее значение связано с инвариантной мерой из системы оператора переноса .

внешние ссылки